匹配渐近展开法(英語:method of matched asymptotic expansions)是数学中用于获得方程或方程组高精度近似解的一种常用方法,尤其常用于奇异摄动微分方程的求解。
对于许多奇异摄动问题而言,可以将定义域分成两个或多个部分。其中一部分(通常是范围最大的部分)可以通过正则摄动理论获得渐近展开级数解。然而这个解在其他较小的部分则十分不精确。如果这些部分处于定义域边界上被称为边界层,处于定义域中间则称为内层。可以将边界层或内层内的求解问题当作一个独立的摄动问题处理,以获得相应的“内解”(之前通过正则摄动获得的则称为“外解”)。最后再将内解与外解通过“匹配”的办法合并,以得到在整个定义域内都适用的近似解。[1][2][3]
考虑边值问题

其中 为时间
为时间 的函数,定义域从0到1,边界条件为
的函数,定义域从0到1,边界条件为 与
与 。
。 是一个小参数,满足
是一个小参数,满足 。
。
由 十分小,故可以当作正则摄动问题处理。取
十分小,故可以当作正则摄动问题处理。取 ,有
,有

该方程的解为

其中 为常数。使用边界条件
为常数。使用边界条件 ,有
,有 。而如果使用另一个边界条件
。而如果使用另一个边界条件 ,则有
,则有 。这说明该解不可能满足所有边界条件,意味着
。这说明该解不可能满足所有边界条件,意味着 的假设不能在整个定义域中都适用(即奇异摄动问题)。于是,我们能够知道定义域中必定存在一个边界层,其中
的假设不能在整个定义域中都适用(即奇异摄动问题)。于是,我们能够知道定义域中必定存在一个边界层,其中 与自变量
与自变量 相比不能再忽略不计。这个边界层位于
相比不能再忽略不计。这个边界层位于 一侧。于是我们使用另一个边界条件
一侧。于是我们使用另一个边界条件 得到适用于边界层以外区域的外解
得到适用于边界层以外区域的外解 。
。
在边界层之内, 与
与 都很小,但它们大小相若,故可以定义一个新的O(1) 时间变量
都很小,但它们大小相若,故可以定义一个新的O(1) 时间变量 。于是原先的边值问题可以改写为
。于是原先的边值问题可以改写为

将两边同乘 再取
再取 ,得到
,得到

该方程的解为

其中 与
与 为常数。使用边界层内的边界条件
为常数。使用边界层内的边界条件 ,得到
,得到 。故内解为
。故内解为

由于对于中间大小的 (
( )需同时满足内解和外解,故可以令内解的外极限与外解的内极限相等,即
)需同时满足内解和外解,故可以令内解的外极限与外解的内极限相等,即 。由此得到常数
。由此得到常数 。
。
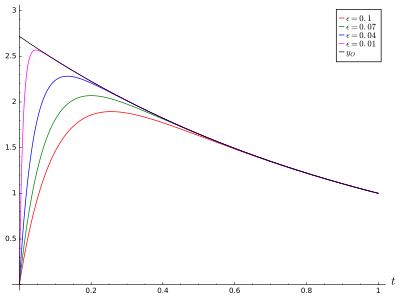
 取不同值时的近似解
取不同值时的近似解
最后,将匹配好的内解与外解合并,以得到适用于整个定义域的近似解。具体而言,即是将内解与外解相加,再减去内、外解重合部分的值 (即外解的内极限,或内解的外极限)。此问题中,重合部分的值为
(即外解的内极限,或内解的外极限)。此问题中,重合部分的值为 。故可以得到原边值问题的最终近似解为
。故可以得到原边值问题的最终近似解为































