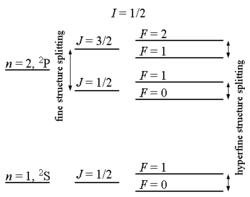
 氫原子的精細結構圖:左邊是波耳的能級線譜,中間是經過修正後,線譜的精細結構,右邊是線譜的超精細結構。
氫原子的精細結構圖:左邊是波耳的能級線譜,中間是經過修正後,線譜的精細結構,右邊是線譜的超精細結構。
在原子物理學裏,因為一階相對論性效應,與自旋-軌道耦合,而產生的原子譜線分裂,稱為精細結構。
非相對論性、不考慮自旋的電子產生的譜線稱為粗略結構。類氫原子的粗略結構只與主量子數 有關;更精確的模型,考慮到相對論效應與自旋-軌道效應,能夠分解能級的簡併,使譜線能更精細地分裂。相對於粗略結構,精細結構是一個
有關;更精確的模型,考慮到相對論效應與自旋-軌道效應,能夠分解能級的簡併,使譜線能更精細地分裂。相對於粗略結構,精細結構是一個 效應;其中,
效應;其中, 是原子序數,
是原子序數, 是精細結構常數。
是精細結構常數。
精細結構修正包括相對論性的動能修正與自旋-軌道修正。整個哈密頓量 是
是
 ;
;
其中, 是零微擾哈密頓量,
是零微擾哈密頓量, 是動能修正,
是動能修正, 是自旋-軌道修正。
是自旋-軌道修正。
相對論性修正[编辑]
經典哈密頓量的動能項目是
 ;
;
其中, 是動能,
是動能, 是動量,
是動量, 是質量。
是質量。
可是,若加入狹義相對論的效應,我們必須使用相對論形式的動能:
 ;
;
其中, 是光速。
是光速。
請注意在這方程式的右手邊,平方根項目是總相對論性能量, 項目是電子的靜能量。假設
項目是電子的靜能量。假設 ,則可以用泰勒級數展開平方根項目:
,則可以用泰勒級數展開平方根項目:
 。
。
哈密頓量的動能修正是
 。
。
將這修正當作一個小微擾,根據量子力學的微擾理論,我們可以計算出相對論性的一階能量修正 :
:
 ;
;
其中, 是主量子數,零微擾波函數
是主量子數,零微擾波函數 是本徵能量為
是本徵能量為 的本徵函數,
的本徵函數, ,精細結構常數
,精細結構常數 。
。
回想零微擾哈密頓量 與
與 的關係方程式:
的關係方程式:
 。
。
零微擾哈密頓量等於動能加上位能 :
:
 。
。
將位能移到公式右手邊:
 。
。
將這結果代入 的公式:
的公式:
![{\displaystyle {\begin{aligned}E_{n}^{(1)}&=-{\frac {1}{8m^{3}c^{2}}}\langle \psi _{n}^{(0)}\vert p^{2}p^{2}\vert \psi _{n}^{(0)}\rangle \\&=-{\frac {1}{8m^{3}c^{2}}}\langle \psi _{n}^{(0)}\vert (2m)^{2}(E_{n}^{(0)}-V)^{2}\vert \psi _{n}^{(0)}\rangle \\&=-{\frac {1}{2mc^{2}}}[(E_{n}^{(0)})^{2}-2E_{n}^{(0)}\langle V\rangle +\langle V^{2}\rangle ]\\\end{aligned}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d2c014d57d5b4b7d7c66265b2b6118df203887a) 。
。
類氫原子的位能是 ;其中,
;其中, 是單位電荷量,
是單位電荷量, 是徑向距離。經過一番繁瑣的運算[1]
,可以得到
是徑向距離。經過一番繁瑣的運算[1]
,可以得到
 ,
, ;
;
其中, 是波耳半徑,
是波耳半徑, 是角量子數。
是角量子數。
將這兩個結果代入,經過一番運算,可以得到相對論修正:
![{\displaystyle {\begin{aligned}E_{n}^{(1)}&=-{\frac {1}{2mc^{2}}}\left[(E_{n}^{(0)})^{2}-2E_{n}^{(0)}{\frac {Z^{2}e^{2}}{4\pi \epsilon _{0}a_{0}n^{2}}}+{\frac {Z^{4}e^{4}}{(l+1/2)(4\pi \epsilon _{0}a_{0})^{2}n^{3}}}\right]\\&=-{\frac {(E_{n}^{(0)})^{2}}{2mc^{2}}}\left({\frac {4n}{l+1/2}}-3\right)\\\end{aligned}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b54c76097b75a554bb61d9a17616059fe326f6ae) 。
。
自旋-軌道修正[编辑]
當我們從標準參考系(原子核的靜止參考系;原子核是不動的,電子運動於它環繞著原子核的軌道)改變至電子的靜止參考系(電子是不動的,原子核運動於它環繞著電子的軌道)時,我們會遇到自旋-軌道修正。在這狀況,運動中的原子核有效地形成了一個電流圈,這會產生磁場 .可是,因為電子的自旋,電子自己擁有磁矩
.可是,因為電子的自旋,電子自己擁有磁矩 。兩個磁向量
。兩個磁向量 與
與 共同耦合.這使得哈密頓量內,又添加了一個項目:
共同耦合.這使得哈密頓量內,又添加了一個項目:
 ;
;
其中, 是真空電容率,
是真空電容率, 是角動量,
是角動量, 是自旋。
是自旋。
設定總角動量 。應用一階微擾理論,由於
。應用一階微擾理論,由於 、
、 、
、 、
、 ,這四個算符都互相對易。
,這四個算符都互相對易。 、
、 、
、 、
、 ,這四個算符也都互相對易。這四個算符的共同本徵函數可以被用為零微擾波函數
,這四個算符也都互相對易。這四個算符的共同本徵函數可以被用為零微擾波函數 ;其中,
;其中, 是總角量子數,
是總角量子數, 是自旋量子數。那麼,經過一番運算,可以得到能級位移
是自旋量子數。那麼,經過一番運算,可以得到能級位移
![{\displaystyle E_{n}^{(1)}={\frac {(E_{n}^{(0)})^{2}}{mc^{2}}}\ {\frac {2n[j(j+1)-l(l+1)-3/4]}{l(l+1)(2l+1)}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8012622497b6f875b639d0a32437fecfc25c658) 。
。
相對論性修正與自旋-軌道修正的總和是
![{\displaystyle E_{n}^{(1)}=-{\frac {(E_{n}^{(0)})^{2}}{2mc^{2}}}\left({\frac {4n}{l+1/2}}-3\right)+{\frac {(E_{n}^{(0)})^{2}}{mc^{2}}}\ {\frac {2n[j(j+1)-l(l+1)-3/4]}{l(l+1)(2l+1)}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/712125e6ef7f938ab1d33d0df10b0ca1f6b9888a) ;
;
其中, 。
。
將 的這兩個數值分別代入總合方程式裏,經過一番運算,可以得到同樣的結果:
的這兩個數值分別代入總合方程式裏,經過一番運算,可以得到同樣的結果:
 。
。
總結,修正後,取至一階,電子的總能級為,
 ;
;
其中, 是電子的基態能級,
是電子的基態能級, 是精細結構常數。
是精細結構常數。
更精确的结果[编辑]
从狄拉克方程直接求解得到的结果是[2]:
![{\displaystyle E_{n}=-mc^{2}\left[1-\left(1+\left[{\dfrac {Z\alpha }{n-j-{\frac {1}{2}}+{\sqrt {\left(j+{\frac {1}{2}}\right)^{2}-Z^{2}\alpha ^{2}}}}}\right]^{2}\right)^{-1/2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/395ad372cc6bbfc2591fbee1d3e5f00dc25b9368)
其一阶近似就是上面的结果。
參考文獻[编辑]
- Liboff, Richard L. Introductory Quantum Mechanics. Addison-Wesley. 2002. ISBN 0-8053-8714-5.
外部連結[编辑]































![{\displaystyle {\begin{aligned}E_{n}^{(1)}&=-{\frac {1}{8m^{3}c^{2}}}\langle \psi _{n}^{(0)}\vert p^{2}p^{2}\vert \psi _{n}^{(0)}\rangle \\&=-{\frac {1}{8m^{3}c^{2}}}\langle \psi _{n}^{(0)}\vert (2m)^{2}(E_{n}^{(0)}-V)^{2}\vert \psi _{n}^{(0)}\rangle \\&=-{\frac {1}{2mc^{2}}}[(E_{n}^{(0)})^{2}-2E_{n}^{(0)}\langle V\rangle +\langle V^{2}\rangle ]\\\end{aligned}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d2c014d57d5b4b7d7c66265b2b6118df203887a)







![{\displaystyle {\begin{aligned}E_{n}^{(1)}&=-{\frac {1}{2mc^{2}}}\left[(E_{n}^{(0)})^{2}-2E_{n}^{(0)}{\frac {Z^{2}e^{2}}{4\pi \epsilon _{0}a_{0}n^{2}}}+{\frac {Z^{4}e^{4}}{(l+1/2)(4\pi \epsilon _{0}a_{0})^{2}n^{3}}}\right]\\&=-{\frac {(E_{n}^{(0)})^{2}}{2mc^{2}}}\left({\frac {4n}{l+1/2}}-3\right)\\\end{aligned}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b54c76097b75a554bb61d9a17616059fe326f6ae)













![{\displaystyle E_{n}^{(1)}={\frac {(E_{n}^{(0)})^{2}}{mc^{2}}}\ {\frac {2n[j(j+1)-l(l+1)-3/4]}{l(l+1)(2l+1)}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8012622497b6f875b639d0a32437fecfc25c658)
![{\displaystyle E_{n}^{(1)}=-{\frac {(E_{n}^{(0)})^{2}}{2mc^{2}}}\left({\frac {4n}{l+1/2}}-3\right)+{\frac {(E_{n}^{(0)})^{2}}{mc^{2}}}\ {\frac {2n[j(j+1)-l(l+1)-3/4]}{l(l+1)(2l+1)}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/712125e6ef7f938ab1d33d0df10b0ca1f6b9888a)





![{\displaystyle E_{n}=-mc^{2}\left[1-\left(1+\left[{\dfrac {Z\alpha }{n-j-{\frac {1}{2}}+{\sqrt {\left(j+{\frac {1}{2}}\right)^{2}-Z^{2}\alpha ^{2}}}}}\right]^{2}\right)^{-1/2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/395ad372cc6bbfc2591fbee1d3e5f00dc25b9368)