迪恩數
迪恩數(D,De或Dn)是流體力學中的無因次量,會用在彎管及彎曲渠道的流體研究中,得名自1920年代研究彎曲流場的英國科學家威廉·雷金納德·迪恩。
物理背景[编辑]
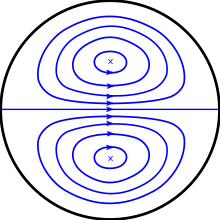
黏性流體沿直管道流動時,管中央的流速較快,近管壁的流速較慢,為泊肅葉流。轉彎時,受離心力影響,中央較快的流體被推到外側(附圖的右側),管壁附近的流體相應被擠壓返回內側(附圖的左側),產生兩個反向的渦旋。此種次要的效應與原先向前的流動互相疊加,所以流體粒子實際的軌跡是螺旋線。[1]:469–470此種渦流稱為迪恩渦(Dean vortices)。
定義[编辑]
迪恩數的定義如下:
- 為流體密度
- 為流體的粘度
- 是軸向的速度值
- 為彎管直徑(若截面不是圓形,可以用等效直徑,請參考雷諾數)
- 是彎管的曲率半徑
迪恩數和雷諾數(基於在直徑d的管內流速為V的流體)及曲率平方根的乘積成正比[2]。
迪恩方程[编辑]
迪恩數出現在迪恩方程中,這是針對牛顿流体在環面管中的軸向均勻流,曲率效應較小 () 時針對纳维-斯托克斯方程的近似。
此處使用正交座標系 ,其單位向量和彎管的中線對齊,延著中線方向,和中線平面垂直,而為副法線.若軸向流是因為壓力梯度而產生,其軸向速度 除以 ,跨流線的速度 除以 ,跨流線的壓力除以,而長度除以曲率半徑。
利用上述的無因次變數及座標,迪恩方程式可以用下式表示[3]
其中
- 為實質導數。
迪恩數D是上述系統中唯一的參數,也包括了曲率效應的第一階效應在內,若要考慮更高階的效應,需要引入其他的參數。
若曲率的影響不大時(D比較小),迪恩方程可以用迪恩數的级数展开來表示. 此處在 (Dennis & Ng 1982)時都還是穩定的[4]。若D值較大,有許多不同的解,其中有許多是不穩定的。
參考資料[编辑]
- ^ Berger, S. A.; Talbot, L.; Yao, L. S. Flow in Curved Pipes. Ann. Rev. Fluid Mech. 1983, 15: 461–512. Bibcode:1983AnRFM..15..461B. doi:10.1146/annurev.fl.15.010183.002333.
- ^ Chapter5 Geometry and Flow p.3 互联网档案馆的存檔,存档日期2016-03-04.
- ^ Mestel, J. Flow in curved pipes: The Dean equations (页面存档备份,存于互联网档案馆), Lecture Handout for Course M4A33, Imperial College.
- ^ Dennis, C. R.; Ng, M. Dual solutions for steady laminar-flow through a curved tube. Q. J. Mech. Appl. Math. 1982, 35: 305. doi:10.1093/qjmam/35.3.305.
- Dean, W. R. Note on the motion of fluid in a curved pipe. Phil. Mag. 1927, 20: 208–223.
- Dean, W. R. The streamline motion of fluid in a curved pipe. Phil. Mag. (7). 1928, 5: 673–695.
| |||||||























