欠 (多面體變換)
外观

欠(Diminish)是一種多面體變換,指從多面體中移除局部的結構,並將被移除的部分以一個新的面取代。[1]例如小斜方截半二十面體欠側台塔是指缺少台塔這種結構的小斜方截半二十面體。欠這種多面體變換通常用於描述詹森多面體,由諾曼·詹森描述詹森多面體時提出[2]。
-
移除了一側五角台塔的小斜方截半二十面體
-
在切去五角台塔處補上十邊形面後形成小斜方截半二十面體欠一側台塔
一般的「欠」操作是指在不添加新的稜的情況下進行的,例如上例的小斜方截半二十面體欠側台塔。也有些「欠」操作會需要添加新的稜,此時的操作類似於截角,但截角通常會是對整體幾何結構所有的相同結構予以移除,而「欠」操作僅移除局部,例如欠四面十二面體正是一個例子,其只移除了正十二面體上的4個四面體結構。[3]
正多面體欠側錐
[编辑]正多面體欠側錐是指移除了正多面體若干側之錐體所形成的幾何形狀。在不添加新的稜的情話下,能夠欠除局部結構的正多面體有正二十面體,其表面上相鄰的每5個三角形都可以視為一個五角錐,因此正二十面體可以欠側錐。
| 正二十面體欠側錐 (五角錐反角柱) |
正二十面體欠對二側錐 (五角反棱柱) |
正二十面體欠鄰二側錐 | 正二十面體欠三側錐 |
|---|---|---|---|

|

|

|

|
均勻多面體欠立體
[编辑]均勻多面體欠立體是指缺少局部幾何結構的均勻多面體。[4]:737可能的立體有均勻多面體欠側錐、均勻多面體欠側帳塔等。
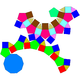
可以欠側帳塔的立體包括截半立方體、截半二十面體、小斜方截半立方體和小斜方截半二十面體。
| 截半立方體欠側帳塔 (三角帳塔) |
截半二十面體欠側帳塔 (五角罩帳) |
小斜方截半立方體欠側帳塔 (四角帳塔柱) |
小斜方截半立方體欠二側帳塔 (八角柱) |
小斜方截半二十面體欠一側台塔 | 小斜方截半二十面體欠對二側帳塔 | 小斜方截半二十面體欠鄰二側帳塔 | 小斜方截半二十面體欠三側台塔 |
|---|---|---|---|---|---|---|---|
| 詹森多面體 (J3) |
詹森多面體 (J6) |
詹森多面體 (J19) |
均勻多面體 | 詹森多面體 (J76) |
詹森多面體 (J80) |
詹森多面體 (J81) |
詹森多面體 (J83) |

|

|

|

|

|

|

|

|

|

|

|
|

|

|
| |
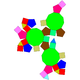
| 移除局部的多面體 | |||||||
| 截半立方體 | 截半二十面体 | 小斜方截半立方体 | 小斜方截半二十面体 | ||||

|

|

|

| ||||
參見
[编辑]參考文獻
[编辑]- ^ Weisstein, Eric W. (编). Diminished Polyhedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8.
- ^ Martin Kraus. tetrahedrally truncated dodecahedron and stellated icosahedron. polyhedra-world.nc. [2023-01-21]. (原始内容存档于2023-01-10).
- ^ Weisstein, E.W. CRC Concise Encyclopedia of Mathematics. CRC Press. 2002. ISBN 9781420035223.[失效連結]



