卡比博-小林-益川矩陣
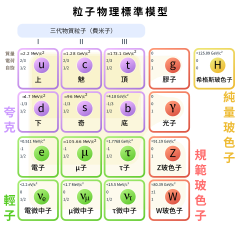
| 粒子物理學標準模型 |
|---|
 |
| 粒子物理學中的味 |
|---|
| 味量子數: |
| 相關量子數: |
| 組合: |
| 味混合 |
卡比博-小林-益川矩陣(Cabibbo-Kobayashi-Maskawa,CKM或KM matrix)是粒子物理標準模型的一個重要組成成份,它表徵了頂類型和底類型夸克間通過W粒子弱相互作用的耦合強度。對二代夸克情形,它是由意大利物理學家卡比博在1963年首先給出的,通常被稱為卡比博矩陣或卡比博角。1973年日本物理學家小林誠和益川敏英把它推廣到三代夸克。三代矩陣含有相位,可以用來解釋弱相互作用中的電荷宇稱對稱性破缺(CP破壞),也被經常用來解釋宇宙重子數不對稱。CKM矩陣在輕子中的對應是牧-中川-坂田矩陣(Maki-Nakagawa-Sakata或MNS)。
內容
[編輯]歷史
[編輯]早期的粒子物理模型包涵三種夸克—上夸克、下夸克和奇異夸克。在研究強子的弱衰變中,人們發現奇異數守恆的過程要比不守恆的過程進行得快約20倍。為解釋此現象,卡比博引入了一個下夸克和奇異夸克(這兩種夸克有相同的量子數)之間的混合角θc[1]。上夸克與下夸克和奇異夸克的相互作用耦合分別正比於此角的餘弦(cosθc)和正弦(sinθc)。實驗上sinθc約為0.23。
1973年,在一篇發表在日本期刊《理論物理學進展》上的題為「弱相互作用可重整化理論中的CP破壞」的論文中,小林誠和益川敏英把卡比博角推廣到三代夸克[2]。他們發現雖然一般的三維幺正矩陣有九個實參數,但是只有四個具有物理意義,而其它的都可以被吸收到夸克波函數的位相中而不為觀測。四個物理參數中的一個是位相因子,它提供了CP破壞的微觀機制,同時猜測了第三代夸克的存在,因此具有重大的物理意義。他們二人也因而與南部陽一郎分享了2008年諾貝爾物理學獎[3][4]。
如今,尋找CKM矩陣參數的微觀物理起源是粒子物理理論研究的重大課題之一。
參數化表示
[編輯]CKM矩陣是一個三維幺正矩陣。 小林誠和益川敏英當初給的表示是[2]:
在標準參數化下,它可以由三個混合角(θ12,θ13,θ23)和一個相位(δ)表示為[5]
其中(u,c,t)和(d,s,b)分別代表三代頂類型(上、粲、頂)和底類型(下、奇異、底)夸克,c12,s12等是cosθ12,sinθ12等的簡寫。 目前實驗給出的數據:
- θ12 = 13.04±0.05°
- θ13 = 0.201±0.011°
- θ23 = 2.38±0.06°
- δ13 = 1.20±0.08
實驗上CKM矩陣參數滿足s13<<s23<<s12<<1。 描寫這一重要特性的一個常用參數化表示是由美國物理學家林肯·沃芬斯坦給出的。記
截止到λ3,CKM矩陣為[6]
么正三角形
[編輯]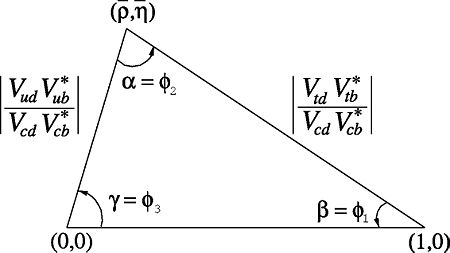
CKM矩陣也可用所謂的幺正三角形來圖像表示。最常見的是正交關係
用測量最精確的項(VcdV*cb)來歸一,此關係可以表示為複平面上的三角形,其三頂點坐標分別為(0,0),(1,0) 和(,),如右圖所示。它的面積與位相參數表示化無關,是刻劃CP破壞的不變量。文獻中稱之為雅爾斯廓格(Jarlskog)不變量。
數學推導
[編輯]CKM矩陣的數學推導相當平庸。首先任意一個三維矩陣可以寫成歐拉形式V=V2V1V3,其中對角塊矩陣V1,V2,V3有以下形式(X代表非零元)
其次注意到任意一個二維幺正矩陣可以表為(ε,η,ρ為幺模複數,c=cosθ,s=sinθ)
由此
因此可以通過一系列對角幺正矩陣作矩陣變換
使得
在上式中V2'仍是與V2同形的一般幺正矩陣, 但可以繼續在V上左、右相乘與V2'和V3'對易的對角矩陣,即 diag(α,β,β)型矩陣(α,β幺模),使得
最後將所有的對角(相位)變換矩陣吸收到夸克波函數中去,V2',V1',V3'相乘即得CKM矩陣。
參數測量
[編輯]CKM矩陣元實驗測定和最新數據的詳細資料,可參閱粒子數據組的網頁和出版物[7]
沃爾芬斯坦參數:
- 和雅爾斯廓格不變量:
獨立變量的計算
[編輯]考慮有 N 代夸克 (2N 種風味),那麼
- 一個 N × N 的么正矩陣需要 N2 個實係數來給定 (因為么正矩陣滿足 VV† = I,其中 V† 是 V 的共軛轉置,而 I 是單位矩陣) 。
- 其中 2N − 1 個係數不是物理上實際的,因為每個夸克都可以吸收一個相位 (質量本徵態和弱作用力本徵態各可吸收一個),而全部的共同相位是不可觀測的。因此,不受相位選擇影響的自由變數總共有 N2 − (2N − 1) = (N − 1)2 個。
- 這其中有 N(N − 1)/2 個是旋轉角度,稱為夸克的混合角。
- 而剩下的 (N − 1)(N − 2)/2 個就是造成 CP破壞的複數相位。
當 N = 2 時,獨立變量只有一個,就是兩代夸克間的混合角。當初只有兩代夸克被發現時,這是第一種 CKM 矩陣。其角度稱為卡比博角度,由尼古拉·卡比博發明。
在標準模型中,N = 3,總共有三個混合角和一個 CP 破壞相位。
與重子生成的關係
[編輯]CP破壞是解釋自宇宙大爆炸以來僅物質存在(即反物質消失)的沙卡洛夫三條件(熱力學非平衡,重子數不守恆,C和CP對稱性不守恆)之一,因此CKM矩陣在粒子宇宙學中有着重要應用。但是現在公認的結論是實驗測量到CP破壞的數量級,遠不足以解釋觀測到的重子不對稱度,因此重子生成必須有其他的來源。
參考資料
[編輯]書籍
[編輯]- 鄭大培,李靈峰. Gauge Theory of Elementary Particle Physics [基本粒子物理的規範理論]. 牛津大學出版社. 1989. ISBN 0-19-851956-7.
- H. Georgi. Weak Interactions and Modern Particle Physics [弱相互作用和現代粒子物理學]. Addison-Wesley. 1984. ISBN 0-8053-3163-8.
論文
[編輯]- ^ N. Cabibbo. Unitary Symmetry and Leptonic Decays. Physical Review Letters. 1963, 10: 531–533.
- ^ 2.0 2.1 M. Kobayashi and T. Maskawa. CP Violation in the Renormalizable Theory of Weak Interaction. Progress in Theoretical Physics. 1973, 49: 652–657.
- ^ The Nobel Prize in Physics 2008. Nobel Foundation. [2008-10-09]. (原始內容存檔於2008-10-08).
- ^ 閆同民. 与2008年诺贝尔物理奖失之交臂的物理学家. 物理雙月刊: 354–357. 2013 [2013-10-02]. (原始內容存檔於2013-10-04). 參數
|journal=與模板{{cite web}}不匹配(建議改用{{cite journal}}或|website=) (幫助);|volume=被忽略 (幫助) - ^ L.L. Chau and W.-Y. Keung. Comments on the Parametrization of the Kobayashi-Maskawa Matrix. Physical Review Letters. 1984, 53: 1802.
- ^ L. Wolfenstein. Parameterization of the Kobayashi-Maskawa Matrix. Physical Review Letters. 1983, 51: 1945–1947.
- ^ K. Nakamura; et al. Review of Particles Physics: The CKM Quark-Mixing Matrix (PDF). Journal of Physics G. 2010, 37 (75021): 150 [2012-11-05]. (原始內容存檔 (PDF)於2018-07-14).
外部連結
[編輯]- 粒子物理數據組(頁面存檔備份,存於網際網路檔案館)首頁
- 康奈爾大學的CLEO(頁面存檔備份,存於網際網路檔案館)實驗
- 高能加速器研究機構 (KEK(頁面存檔備份,存於網際網路檔案館)) 的 BELLE(頁面存檔備份,存於網際網路檔案館) 實驗
- SLAC國家加速器實驗室 (SLAC(頁面存檔備份,存於網際網路檔案館)) 的 BaBar(頁面存檔備份,存於網際網路檔案館) 實驗
- 費米國家加速器實驗室(FNAL(頁面存檔備份,存於網際網路檔案館))的D0(頁面存檔備份,存於網際網路檔案館)和CDF(頁面存檔備份,存於網際網路檔案館)實驗
- 歐洲核子研究中心(CERN(頁面存檔備份,存於網際網路檔案館))的LHCb(頁面存檔備份,存於網際網路檔案館) 實驗




![{\displaystyle s_{13}e^{i\delta }=V_{ub}^{*}=A\lambda ^{3}(\rho +i\eta )={\frac {A\lambda ^{3}({\bar {\rho }}+i{\bar {\eta }})(1-A^{2}\lambda ^{4})^{1/2}}{(1-\lambda ^{2})^{1/2}[1-A^{2}\lambda ^{4}({\bar {\rho }}+i{\bar {\eta }})]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97465ac2d4e646e7f3f2bf365bd28ceb7aaf7908)












