 極移量隨時間的變化,其中極移量的單位是角秒(0.1角秒約合3米),時間的單位是儒略日[1]
極移量隨時間的變化,其中極移量的單位是角秒(0.1角秒約合3米),時間的單位是儒略日[1]
極移,或稱地極移動,是指因地球自轉軸在地球體內位置的變化而形成的地極點在地球表面上的位置發生變化的現象。[2][3]地球自轉軸與地面的交點稱為地極點。地球表面的物質運動(如洋流、海潮等)以及地球內部的物質運動(如地幔運動),都會使極點的位置產生變化。[4]地極點所處的瞬時位置被稱為瞬時極,而某一時間段內極點的平均位置被稱為平均極。極移會對以地球北極為基點的地心地固坐標系(ECEF)造成影響,使其坐標軸指向發生變化。這種變化通常是緩慢且微小的,大致表現為瞬時極在一個直徑約0.5角秒的圓上繞平均極以逆時針方向旋轉。
與歲差和章動不同,極移是地球坐標系本身的變動,它會使地表各測站的天文坐標發生變化,但不會影響天體在天球坐標系中的坐標。極移和歲差、章動及日長變化一同構成了地球定向參數(EOP)。[5]
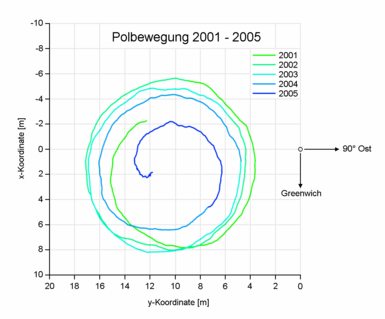 2001年至2005年地極的移動,國際協議原點位於圖中右側,X軸正向指向下方,Y軸正向指向左方
2001年至2005年地極的移動,國際協議原點位於圖中右側,X軸正向指向下方,Y軸正向指向左方地極坐標是表達瞬時極與平均極相對位置的一種方式。這一坐標將平均極作為原點,並以一對正交的子午線分別作為該坐標系的X軸和Y軸。在國際地球自轉服務(IERS)提供的瞬時極坐標中,原點採用IERS參考極(IRP),X軸正向為本初子午線,Y軸正向為270°經線。IERS參考極與國際協議原點(CIO)存在着  的差異。[6]
的差異。[6]
極移由三個主要成分組成。其一是周期約435天的自由擺動,也被稱為錢德勒擺動,其方向為逆時針,幅度平均為0.15秒。其二是由空氣和水團的季節性分布變化所引起的受迫擺動,其周期為一年,方向亦為逆時針,幅度平均為0.10秒。其三是朝西經80°方向的不規則漂移,平均速率為每年約0.0035秒。前兩個成分都與圓周運動近似,它們的疊加使得瞬時極的軌跡呈現出具有明顯特徵跳動形狀。[7]
除了上述三個主要成分外,極移還存在着由海洋潮汐和由引力矩引起的周期性變化,前者的周期不足一日,後者的周期不足兩日。[8]
將地球視為剛體計算得到的極移周期又稱歐拉周期(英語:the Euler period),其長度約為305天,比錢德勒擺動的周期略短。[9]對於剛性地球,其旋轉的性質可以通過歐拉動力學方程予以描述。
由歐拉動力學方程,剛性地球的角動量  、轉動向量
、轉動向量  、角動量的變化速率
、角動量的變化速率 ,和其所受的合外力矩
,和其所受的合外力矩  存在如下關係:
存在如下關係:

以各坐標的分量進行表達,將上式進行展開,可以得到:

其中,  、
、 及
及  表示地球相對於地固坐標系的三個坐標軸的轉動慣量。這三個轉動慣量隱含在角動量
表示地球相對於地固坐標系的三個坐標軸的轉動慣量。這三個轉動慣量隱含在角動量  和慣性張量
和慣性張量  的關係中,即:
的關係中,即:

若選取地固坐標系的主中心慣性軸為坐標軸的Z軸,且坐標系的原點在地球質心上,由旋轉對稱性可以得到  。[10]此時,從歐拉動力學方程能夠導出:
。[10]此時,從歐拉動力學方程能夠導出:

在地球不受外力矩作用的情況,即  的情況下,上述方程組變為:
的情況下,上述方程組變為:

第三條方程式表明了  是個常數,且與地球自轉的角速率
是個常數,且與地球自轉的角速率  相等。對前兩條方程式,可以進一步求偏導:
相等。對前兩條方程式,可以進一步求偏導:

由前一方程組的第二式還可得到  ,代入後一方程組的第一式,可得到二階的常微分方程組:
,代入後一方程組的第一式,可得到二階的常微分方程組:
![{\displaystyle {\begin{cases}{\ddot {\omega }}_{1}+{\left[{\frac {C-A}{A}}\Omega \right]}^{2}\omega _{1}=0\\{\ddot {\omega }}_{2}+{\left[{\frac {C-A}{A}}\Omega \right]}^{2}\omega _{2}=0\\\end{cases}}\Longrightarrow {\begin{cases}\omega _{1}=p\cos {\left[({\frac {C-A}{A}}\Omega )t+\varphi _{0}\right]}\\\omega _{2}=p\sin {\left[({\frac {C-A}{A}}\Omega )t+\varphi _{0}\right]}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/823832b07efeae0fdfcc2ee1cd8f9cc0ed7bd61b)
右側的方程組是左側方程組的解,其中的  是常係數,
是常係數, 是表示初始相位的常數,上式還可表示為:
是表示初始相位的常數,上式還可表示為:
![{\displaystyle {\begin{cases}\lVert {\vec {\omega }}\rVert ={\sqrt {\Omega ^{2}+p^{2}}}\\{\vec {e_{\omega }}}={\left[{\frac {\omega _{1}}{\omega }},{\frac {\omega _{2}}{\omega }},{\frac {\Omega }{\omega }}\right]}^{\text{T}}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8842e21368dc666a70335d6bc49b9c6c2097907c)
上式表明,在無外力作用的情況下,地球的自轉軸仍會圍繞主中心慣性軸以常速率  作圓周運動,且其與主中心慣性軸的夾角是恆定的。這一速率即為歐拉周期所對應的頻率。值得注意的是,這一擺動是地球自轉軸在地球體內部的自由擺動(英語:free wobble),其轉動的軸線是地固坐標系下的慣性軸而非天球坐標系中的某一軸線。因此,這類運動不會影響春分點和天體在天球坐標系中的坐標,與歲差和章動存在本質的區別。[3]
作圓周運動,且其與主中心慣性軸的夾角是恆定的。這一速率即為歐拉周期所對應的頻率。值得注意的是,這一擺動是地球自轉軸在地球體內部的自由擺動(英語:free wobble),其轉動的軸線是地固坐標系下的慣性軸而非天球坐標系中的某一軸線。因此,這類運動不會影響春分點和天體在天球坐標系中的坐標,與歲差和章動存在本質的區別。[3]
從1900年以來,極點漂移了大約20米,部分可以歸責於地核、地幔的運動,還有類似冰川融解所造成的水體的重分配,以及地殼均衡的反彈,即過去承擔冰川或冰床的土地緩慢上升[11]。
- ^ Folgueira, M. Free polar motion of a triaxial and elastic body in Hamiltonian formalism: Application to the Earth and Mars (PDF). Astron. Astrophys. 2005, 432 (3): 1101–1113 [2020-03-24]. Bibcode:2005A&A...432.1101F. doi:10.1051/0004-6361:20041312. (原始內容存檔 (PDF)於2020-05-29).
- ^ 孔祥元; 郭際明; 劉宗泉. 大地测量学基础. 武漢大學出版社. : 164 – 165. ISBN 978-7-30-707562-7.
- ^ 3.0 3.1 李征航; 魏二虎; 王正濤; 彭碧波. 空间大地测量学. 武漢大學出版社. : 62 – 66. ISBN 978-7-30-707574-0.
- ^ 書名: 《GPS測量與數據處理》作者: 李征航,黃勁松編著 當前第:36頁
- ^ The Earth Orientation Parameters. IERS. [2020-03-24]. (原始內容存檔於2021-03-17).
- ^ Dennis D. McCarthy; U.S. Naval Observatory. IERS Conventions (1996). IERS Conventions Centre. [2020-03-24]. (原始內容存檔於2020-03-24).
- ^ Polar motion. IERS. [2020-03-24]. (原始內容存檔於2021-01-25).
- ^ Gérard Petit; Brian Luzum. IERS Conventions (2010) (PDF). IERS Conventions Centre. [2020-03-24]. (原始內容存檔 (PDF)於2021-02-03).
- ^ Polar Motion - an overview | ScienceDirect Topics. www.sciencedirect.com. [2020-03-31]. (原始內容存檔於2021-08-05) (英語).
- ^ 寧津生. 管澤霖 , 編. 地球形状及外部重力场. 測繪出版社. 1981: 205.
- ^ Munk, Walter (2002)























![{\displaystyle {\begin{cases}{\ddot {\omega }}_{1}+{\left[{\frac {C-A}{A}}\Omega \right]}^{2}\omega _{1}=0\\{\ddot {\omega }}_{2}+{\left[{\frac {C-A}{A}}\Omega \right]}^{2}\omega _{2}=0\\\end{cases}}\Longrightarrow {\begin{cases}\omega _{1}=p\cos {\left[({\frac {C-A}{A}}\Omega )t+\varphi _{0}\right]}\\\omega _{2}=p\sin {\left[({\frac {C-A}{A}}\Omega )t+\varphi _{0}\right]}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/823832b07efeae0fdfcc2ee1cd8f9cc0ed7bd61b)


![{\displaystyle {\begin{cases}\lVert {\vec {\omega }}\rVert ={\sqrt {\Omega ^{2}+p^{2}}}\\{\vec {e_{\omega }}}={\left[{\frac {\omega _{1}}{\omega }},{\frac {\omega _{2}}{\omega }},{\frac {\Omega }{\omega }}\right]}^{\text{T}}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8842e21368dc666a70335d6bc49b9c6c2097907c)
