米-門二氏動力學

米氏方程

米-門二氏動力學（英語：Michaelis-Menten kinetics），又稱米氏動力學，以德國生物化學家萊昂諾爾·米夏埃利斯和加拿大醫師莫德·門滕的名字命名，是酶動力學中一個極為重要的方程，可以描述多種非變異構酶動力學現象，其表示式為：
$V_{0}=V_{max}{\frac {[S]}{K_{M}+[S]}}$

方程與推導

以下米氏方程的推導是由喬治·愛德華·布里格斯和約翰·伯頓·桑德森·霍爾丹在1925年提出的：

假設有下圖所示的酶促反應

$E+S{\begin{matrix}k_{1}\\\longrightarrow \\\longleftarrow \\k_{-1}\end{matrix}}ES{\begin{matrix}k_{2}\\\longrightarrow \\\ \end{matrix}}E+P$

假設此酶促反應不可逆，反應產物不和酶結合；k2<k-1, E+S⇌ES 之間的平衡迅速建立達到平衡態（Steady-state），也就是受質和酶的化合物（ES）的濃度不變；建立平衡態所消耗的受質的量很小，可以忽略。這樣有以下關係：

${\frac {d[ES]}{dt}}=k_{1}[E][S]-k_{-1}[ES]-k_{2}[ES]=0$

$[ES]={\frac {k_{1}[E][S]}{k_{-1}+k_{2}}}$

米氏常數Km的定義為：

$K_{M}={\frac {k_{-1}+k_{2}}{k_{1}}}$

原式可簡化為：

$[ES]={\frac {[E][S]}{K_{M}}}$ (1)

總的酶的濃度[E₀]等於自由酶[E]與酶-受質化合物[ES]的和，則有以下關係：

$[E_{0}]=[E]+[ES]$

$[E]=[E_{0}]-[ES]$ (2)

將（2）式代入（1）：

$[ES]={\frac {([E_{0}]-[ES])[S]}{K_{M}}}$

整理得:

$[ES]{\frac {K_{M}}{[S]}}=[E_{0}]-[ES]$

$[ES](1+{\frac {K_{M}}{[S]}})=[E_{0}]$

$[ES]=[E_{0}]{\frac {1}{1+{\frac {K_{M}}{[S]}}}}$ (3)

下式可以描述該酶促反應的速率：

${\frac {d[P]}{dt}}=k_{2}[ES]$ (4)

將 (3) 代入 (4)，分號上下同時乘以[S]得：

${\frac {d[P]}{dt}}=k_{2}[E_{0}]{\frac {[S]}{K_{M}+[S]}}=V_{max}{\frac {[S]}{K_{M}+[S]}}$
或
$V_{0}=V_{max}{\frac {[S]}{K_{M}+[S]}}$

該式可通過非線性作圖或Lineweaver-Burk（雙倒數作圖），Eadie-Hofstee等作圖法變換為線性圖進行分析。

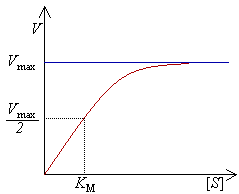
用Vmax＝100，K_M=10繪製的米氏方程的圖像。

在推導過程中幾點需要注意：

• [E₀]是總的酶的量。反應中酶-底物配合物的量[ES]是極不好測量的，所以式子必須寫成[E₀]表示的形式，因為試驗中所用的酶的量是已知的。

• d[P]/dt(V₀, 反應初速度），是試驗中測得的產物生成的初速度，一般是酶促反應在反應開始的幾秒鐘到幾分鐘之內的速度，在這段時間內底物的真實濃度幾乎和底物最初的濃度相同([S]≈[S₀])。

• k₂[E₀]（Vmax） 是酶促反應在給定的酶的量下的最大速度（當所有的酶都在酶-底物配合物的狀態下）。k₂有時也寫為kcat。

作用

• 米氏常數是酶的特徵性物理常數。
• 從K_M可判斷酶的專一性和天然底物。
• 進行酶活力測定時通常選10K_M。
• 底物濃度較低時，K_M可判斷底物走哪一條代謝途徑。

試驗方法

要測得方程中的K_M和Vmax，需要在酶的量[E₀]恆定並已知的情況下，在不同的底物濃度[S]下測得反應的初速度V₀，用非線性作圖或線性作圖的方法求得K_M和Vmax。

K_M反映了底物和酶結合的緊密程度，Vmax反映了酶催化反應的速度。