非線性偏微分方程列表

非線性偏微分方程的在物理學、氣動力學、流體力學、大氣物理、海洋物理、爆炸物理、化學、生理學、生物學、生態學等領域都有重要的應用。非線性偏微分方程的研究，是當前微分方程研究的中心。求解非線性偏微分方程比求解線性偏微分方程，難度大的多，大多數非線性偏微分方程只能依靠數值解法。但多年來數學家們發現了一些行之有效的求解非線性偏微分方程的構造性解法，如反散射法、達布變換法，tanh、雅可比函數展開法等，得出非線性偏微分方程的解析解。解非線性偏微分方程，過程複雜，多數得力於Maple、Mathematica、Matlab等商用計算機代數系統。

已知的非線性偏微分方程，數目不下3000餘種，但有名的不過一百多種，多以發現者命名。

分離變數法

可以藉代數來將方程式重新編排，讓方程式的一部分只含有一個變量，而剩餘部分則跟此變量無關。這樣，隔離出的兩個部分的值，都分別等於常數，而兩個部分的值的代數和等於零。

反散射法

達布變換

混合指數法

齊次平衡法

Tanh 函數展開法

Tanh 函數展開法是求解非線性偏微分方程行波解的重要方法。

設一個非線性偏微分方程可以用下列表述：

$\psi (u,u_{t},u_{x},u_{tt},u_{xx},u_{tx})=0$

作變數代換：

$u(x,t)$ -> $U(\xi )$

$\xi =k*(x-c*t)$

得到：

$\psi (U(\psi ),-kc*{\frac {\partial U}{\partial \psi }},k*{\frac {\partial U}{\partial \psi }},$ $k^{2}*c^{2}*{\frac {\partial ^{2}U}{\partial \psi ^{2}}}$ $,k^{2}*{\frac {\partial ^{2}U}{\partial \psi ^{2}}},-k^{3}*c^{3}*{\frac {\partial ^{3}U}{\partial \psi ^{3}}},k^{3}*{\frac {\partial ^{3}U}{\partial \psi ^{3}}})=0$

1992年數學家 Malfliet 首先應用 tanh 展開法^[1]

對稱分析

Lax 可積系統

Equation	中文	方程
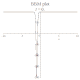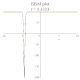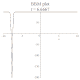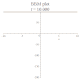
BBM	班傑明-小野方程	: $u_{t}+u_{x}+uu_{x}-u_{xxt}=0.\,$
Belousov-Zhabotinsky	別洛烏索夫-扎伯廷斯基方程	$u_{t}=du_{xx}+u(1-ru-u)$ , $v_{t}=v_{xx}-su*v$
(Benjamin-Ono equation	本傑明-小野方程	$u_{tt}+\alpha (u^{2})_{xx}-\beta u_{xxxx}=0$
Bogoyavlenski-Konoplechenko	波格雅夫連斯基-科譳普勒琛科方程	$u_{xt}+\alpha u_{xxxx}+\beta u_{xxxy}$ $+6\alpha u_{xx}u_{x}+4\beta u_{xy}u_{x}+\beta u_{xx}u_{y}=0$
Born-Infeld	玻恩-英費爾德方程	$\displaystyle (1-u_{t}^{2})u_{xx}+2u_{x}u_{t}u_{xt}-(1+u_{x}^{2})u_{tt}=0$
Boussinesq	博欣內斯克方程	${\frac {\partial ^{2}u}{\partial t^{2}}}-{\frac {\partial ^{2}u}{\partial x^{2}}}-{\frac {\partial ^{2}u^{2}}{\partial ^{2}y^{2}}}+{\frac {\partial ^{4}u}{\partial x^{4}}}=0$
Boussinesa type	博欣內斯克型方程	$u_{tt}-u_{xx}-2\alpha (uu_{x})_{x}-\beta u_{xxtt}=0$
Unnormalized Boussinesq	非規範博欣內斯克方程	$u_{tt}-\alpha (uu_{x})_{x}-\beta *u_{xxxx}=0$
Broer-Kaup	布羅爾-庫普方程組	$u_{y,t}+(2uu_{x})_{x}+2v_{xx}-u_{xxy}=0$ $v_{t}+2(vu)_{x}+v_{xx}=0$
Burgers	伯格斯方程	${\frac {\partial u(x,t)}{\partial t}}+u(x,t){\frac {\partial (u(x,t)}{\partial x}}-nu{\frac {\partial ^{2}(u(x,t)}{\partial x^{2}}}=0$
Burgers-Fisher	伯格斯-費希爾方程	: ${\frac {\partial u}{\partial t}}+u^{2}{\frac {\partial u}{\partial x}}-{\frac {\partial ^{2}u}{\partial u^{2}}}=u(1-u^{2})$
Modified Burgers	變形伯格斯方程	$u_{t}+{\frac {k}{t}}u+buu_{x}=au_{xx}$
Unnormalized Burgers	非規範伯格斯方程	$u_{t}-\alpha u_{xx}-\beta u*u_{x}=0$
Generalized Burgers	廣義伯格斯方程
Burgers-Huxley	伯格斯-赫胥黎方程	$u[t]-nuu[x,x]+auu[x]=bu(1-u)(u-c)$
Bretherton	布雷瑟頓方程	$u_{tt}+u_{xx}+u_{xxxx}-\alpha *u^{3}=0$
Cahn-Hilliard	卡恩-希利亞德方程
Cassama-Holm	卡馬薩-霍爾姆方程	: $u_{t}+2\kappa u_{x}-u_{xxt}+3uu_{x}=2u_{x}u_{xx}+uu_{xxx}$
Chaffee-Infante	查菲 - 堙方特方程	$u_{t}-u_{xx}+\lambda *(u^{3}-u)=0$
Chaplygin	查普里金方程	$0.5u_{tt}+u_{x}u_{xt}-u_{t}*u_{xx}=0$
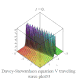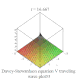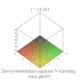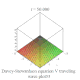
Davey–Stewartson	戴維-斯圖爾森方程組	: $iu_{t}+c_{0}u_{xx}+u_{yy}=c_{1}\|u\|^{2}u+c_{2}u\phi _{x},\,$ $\phi _{xx}+c_{3}\phi _{yy}=(\|u\|^{2})_{x}.\,$
Degasperis-Procesi	DP 方程	$\displaystyle u_{t}-u_{xxt}+2\kappa u_{x}+4uu_{x}=3u_{x}u_{xx}+uu_{xxx}$
Drinfeld-Solokov-Wilson	DSW 方程	${\frac {\partial u}{\partial t}}+3v{\frac {\partial v}{\partial x}}=0$ ${\frac {\partial v}{\partial t}}-2{\frac {\partial ^{3}v}{\partial x^{3}}}+{\frac {\partial u}{\partial x}}v+2u*{\frac {\partial v}{\partial x}}$
Dodd-Bullough-Mikhailov	多德-布洛-米哈伊洛夫方程	[[ $u_{xt}+\alpha e^{u}+\gamma e^{-2*u}=0$
Nonlinear Diffusion	非線性擴散方程	$u_{t}=\alpha u_{xx}-\beta u^{3}-\gamma *u^{2}$
Harry Dym	迪姆方程	: $u_{t}=u^{3}u_{xxx}.\,$
Eckhaus	艾克豪斯方程	$u(x,y,t)_{t}+v(x,t)_{x}+1.0u(x,y,t)(u(x,y,t)_{x})=0$ $v(x,t)_{xt}+u(x,y,t)_{xx}v(x,t)+$ $2u(x,y,t)_{x}v(x,t)_{x}+u(x,y,t)(v(x,t)_{xx}+$ $u(x,y,t)_{xx}+u(x,y,t)_{xxxx}+u(x,y,t)_{yy}=0$
Eikonal	程函方程	$sys:=(u(x,t)_{t}))^{2}+(u(x,t)_{x})^{2}-4=0$
Estevez-Mansfield-Clarkson	埃斯特韋斯-曼斯菲爾德-克拉克森方程	$u_{tyyy}+\beta u_{y}u_{yt}+\beta u_{yy}u_{t}+u_{tt}=0$
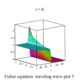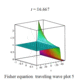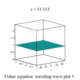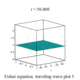
Fitzhugh-Nagumo	菲茨休 - 南雲方程	${\frac {\partial u}{\partial t}}=D{\frac {\partial ^{2}u}{\partial ^{2}x^{2}}}-u(1-u)*(a-u)$
Fisher	費希爾方程	$u_{t}=u_{xx}+au(1-u)$
Fisher-Kolmogorov	費希爾-柯爾莫哥洛夫方程	:: ${\frac {\partial u}{\partial t}}={\frac {\alpha }{k}}*u(1-u^{q})+{\frac {\partial ^{2}u}{\partial x^{2}}}.\,$
Fujita-Storm	藤田-斯托姆方程	$u_{t}=a(u^{-2}u_{x})_{x}$
Gardner	加德納方程	${\frac {\partial u}{\partial t}}+(2au-3bu^{2})*{\frac {\partial u}{\partial x}}+{\frac {\partial ^{3}u}{\partial x^{3}}}=0$
Gibbons-Tsarev	吉本斯-查理夫方程	$u_{t}u_{xt}-u_{x}u_{tt}+u_{xx}+1=0$
Ginzburg-Landau	金茲堡－朗道方程	${\frac {\partial u}{\partial t}}-au{\frac {\partial ^{2}u}{\partial x^{2}}}-bu+c\|u\|^{2}*u=0$
Hirota Satsuma	廣田-薩摩方程組	: $u_{t}-0.5*u_{xxx}+3uu_{x}-3(vw)_{x}=0$ $v_{t}+v_{xxx}-3uv_{x}=0$ $w_{t}+w_{xxx}-3uw_{x}=0$
Hunt-Saxton	亨特 - 薩克斯頓方程	: $(u_{t}+uu_{x})_{x}={\frac {1}{2}}\,u_{x}^{2}$
Ito	伊藤方程	$U_{t}+((6U^{5}+10\alpha (U^{2}U_{xx}+U*U_{x}^{2})+U_{xxxx})_{x}=0$
KdV	KdV方程	: $\partial _{t}\phi +6\phi \partial _{x}\phi +\partial _{x}^{3}\phi =0$
Modified KdV	MKdV方程	$u_{t}+\alpha u^{2}u_{x}+u_{xxx}=0$
KdV-mKdV	KdV-mKdV方程	$u_{t}+6\alpha uu_{x}+6\beta u^{2}u_{}+\gamma *U_{xxx}=0$
KdV-Burgers	KdV-Burgers方程	$u_{t}+uu_{x}-\alpha u_{xx}-\beta *u_{xxx}=0$
Modified KdV-Burgers	變形KdV-Burgers方程	$u_{t}+u_{xxx}-\alpha u^{2}u_{x}-\beta *u_{xx}=0$
Fifth order KdV	五階KdV方程	$u_{t}+\alpha u^{2}u_{x}+\beta u_{x}u_{xx}+\gamma uu_{xxx}+\delta *u_{xxxxx}=0$
Fifth order dispersion KdV	五階色散KdV方程	$u_{t}+\alpha uu_{x}+\beta *u_{xxx}+u_{xxxxx}=0$
Seventh order KdV	七階KdV方程	$U[t]+6UU[x]+U[x,x,x]-U[x,x,x,x,x]+\alpha *U[x,x,x,x,x,x,x,x,x]=0$
Nineth order KdV	九階KdV方程	$U[t]+6UU[x]+U[x,x,x]-U[x,x,x,x,x]+\alpha U[x,x,x,x,x,x,x]+\beta U[x,x,x,x,x,x,x,x,x]=0$
Unnormalized KdV equation	非規範KdV方程	$u_{t}+\alpha u_{xxx}+\beta u*u_{x}=0$
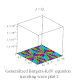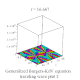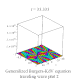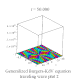
Generalized Burgers-KdV	廣義伯格斯-KdV方程	$U[t]-\alpha {\frac {\partial ^{n}u(x,t)}{\partial x^{n}}}-\beta u(x,t)*{\frac {\partial u(x,t)}{\partial x}}=0$
Unnormalized modified KdV	非規範變形KdV方程	$u_{t}+u_{xxx}+\alpha u^{2}u_{x}=0$
von Karman	馮·卡門方程	$\Delta \Delta (u)=a((w_{xy})^{2}-w_{xx}w_{yy})$ $\Delta \Delta (w)=b(u_{yy}w_{xx}+u_{xx}w_{yy}-2u_{xy}w_{xy})+c$

參考文獻

^ W. Malfliet, Solitary Wave Solution of Nonlinear wave equation, Am J.of Physics 60(7) 1992,650-654

*谷超豪《孤立子理論中的達布變換及其幾何應用》上海科學技術出版社
*閻振亞著《複雜非線性波的構造性理論及其應用》科學出版社 2007年
李志斌編著《非線性數學物理方程的行波解》科學出版社
王東明著《消去法及其應用》科學出版社 2002
*何青王麗芬編著《Maple 教程》科學出版社 2010 ISBN 9787030177445
Andrei D. Polyanin,Valentin F. Zaitsev, HANDBOOK OF NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS, SECOND EDITION CRC PRESS
Graham W. Griffiths William E.Shiesser Traveling Wave Analysis of Partial Differential p135 Equations Academy Press
Richard H. Enns George C. McCGuire, Nonlinear Physics Birkhauser,1997
Inna Shingareva, Carlos Lizárraga-Celaya,Solving Nonlinear Partial Differential Equations with Maple Springer.
Eryk Infeld and George Rowlands,Nonlinear Waves,Solitons and Chaos,Cambridge 2000
Saber Elaydi,An Introduction to Difference Equationns, Springer 2000
Dongming Wang, Elimination Practice,Imperial College Press 2004
David Betounes, Partial Differential Equations for Computational Science: With Maple and Vector Analysis Springer, 1998 ISBN 9780387983004
T.Roubicek: Nonlinear Partial Differential Equations with Applications, 2nd ed., Birkhäuser, Basel, 2013, ISBN 978-3-0348-0512-4.
George Articolo Partial Differential Equations & Boundary Value Problems with Maple V Academic Press 1998 ISBN 9780120644759

外部連結

牛津大學非線性偏微分方程研究中心（頁面存檔備份，存於網際網路檔案館）

[1] W. Malfliet, Solitary Wave Solution of Nonlinear wave equation, Am J.of Physics 60(7) 1992,650-654

[1]