相等

在數學的領域中，若兩個數學對象在各個方面都相同，則稱他們是相等的。這就定義了一個二元謂詞等於，寫作「$=$」；$x=y$當且僅當$x$和$y$相等。通常意義上，等於是通過兩個元素間的等價關係來構造的。將兩個表達式用等於符號連起來，就構成了等式，例如$6-2=4$，即$6-2$與$4$是相等的。

注意，有些時候「$A=B$」並不表示等式。例如，$T(n)=O(n^{2})$表示在數量級$n^{2}$上漸進。因為這裡的符號「$=$」不滿足若且唯若的定義，所以它不等於等於符號；實際上，$O(n^{2})=T(n)$是沒有意義的。請參見大O符號了解這部分內容。

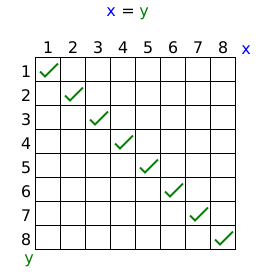等價二元關係的表格

集合$A$上的等於關係是種二元關係，滿足自反性，對稱性，反對稱性和傳遞性。 實際上，這是$A$ 上唯一滿足所有這些性質的關係。 去掉對反對稱性的要求，就是等價關係。 相應的，給定任意等價關係$R$，可以構造商集$A/R$，並且這個等價關係將『下降為』$A/R$上的等於。

在任何條件下都成立的等式稱為恆等式，包含未知數的等式稱為方程式。

邏輯形式

謂詞邏輯含有標準的關於相等的公理來形式化萊布尼茨律。萊布尼茨律是由哲學家萊布尼茨在17世紀提出來的。 萊布尼茨的想法是，兩樣物體是同一的，當且僅當它們有完全相同的性質。 形式化這一說法，可以寫成

對任意$x$和$y$，$x=y$當且僅當對任意謂詞$P$ ，$P(x)$當且僅當$P(y)$。

然而，在一階邏輯中，不能對謂詞進行量化。因此，需要使用下述公理：

對任意$x$和$y$，若$x$等於$y$，則$P(x)$當且僅當$P(y)$。

這條公理對任意單變量的謂詞$P$都有效，但只定義了萊布尼茨律的一個方向：若$x$和$y$相等，則它們具有相同的性質。 可以通過簡單的假設來定義萊布尼茨律的另一個方向：

對任意$x$，$x$等於$x$。

則若$x$和$y$具有相同的性質，則特定的它們關於謂詞$P$是相同的。這裡謂詞$P$為：$P(z)$當且僅當$x=z$。 由於$P(x)$成立，$P(y)$必定也成立（相同的性質），所以$x=y$（' '$P$的變量為$y$）.

等於的一些基本性質

替代性

參見：等量公理

對任意量$a$和$b$和任意表達式$F(x)$，若$a=b$，則$F(a)=F(b)$（設等式兩邊都有意義）。 在一階邏輯中，不能量化像$F$這樣的表達式（它可能是個函數謂詞）。 一些例子：

• 對任意實數$a,b,c$，若$a=b$，則$a+c=b+c$（這裡$F(x)$為$x+c$）
• 對任意實數$a,b,c$，若$a=b$，則$a-c=b-c$（這裡$F(x)$為$x-c$）
• 對任意實數$a,b,c$，若$a=b$，則$ac=bc$（這裡$F(x)$為$xc$）
• 對任意實數$a,b,c$，若$a=b$且$c\neq 0$，則$a/c=b/c$（這裡$F(x)$為$x/c$）

自反性

對任意量$a$，$a=a$。

這個性質通常在數學證明中作為中間步驟。

對稱性

例子：如果$a=b$，那麼$b=a$

傳遞性

例子：如果$a=b$，$b=c$，那麼$a=c$

實數或其他對象上的二元關係「約等於」，即使進行精確定義，也不具有傳遞性（即使看上去有，但許多小的差能夠疊加成非常大）。然而，在絕大多數情況下，等於具有傳遞性。

儘管對稱性和傳遞性通常看上去是基本性質，但它們能夠通過替代性和自反性證明得到。

符號的歷史

主條目：等號

「等於」符號或 「$=$」被用來表示一些算術運算的結果，是由羅伯特·雷科德在1557年發明的。

由於覺得書寫文字過於麻煩，雷科德在他的作品 The Whetstone of Witte 中採用了這一符號。原因是符號中的兩條線一樣長，表明其連接的兩個量也相等。這一發明在威爾士的St Mary教堂有記錄。

約等於的符號是$\approx$或≒，不等於的符號是$\neq$。

參見

• 等號

外部連結

• 關係符號的早期使用（英文）