可壓縮流
可壓縮流是一種氣流,而且此類氣流密度會出現顯着變化。儘管所有氣流都是可壓縮的,但是當馬赫數(流速與聲速的比值)小於0.3時,因為速度造成的密度變化通常小於5%,此時氣流會視為不可壓縮流。 [1]可壓縮流的研究與高速飛機、噴射引擎、火箭引擎、高速進入行星大氣、天然氣管道、商業應用(例如噴砂處理)以及許多其他領域有關。
歷史
[編輯]氣體動力學研究與航天發展息息相關,現代飛機的高速飛行、太空飛行器的大氣重返等問題,以往都未曾深入研究。但其實早在19世紀初,就曾有分析發射子彈氣體改變,從而提高了槍支和大炮的準確性和能力。 [2]隨着時間推移,諸如古斯塔夫·德拉瓦等發明家推動了這一領域的發展,而諸如恩斯特·馬赫(Ernst Mach)等研究人員則試圖透過實驗來了解所涉及的物理現象。
20世紀初,氣體動力學的研究重點轉移到了航空領域。路德維希·普朗托和他的學生提出了重要的概念,從邊界層到超音速震波,超音速風洞和超音速噴嘴設計。 [2]普朗托大學的學生西奧多·馮·卡門繼續提高對超音速流動的理解。其他著名人物:西奧多·梅耶、Luigi Crocco和Shapiro,也為現代氣體動力學研究基礎做出了重要貢獻。
隨着20世紀初期人們對氣體動力學的理解提高,人們誤以為飛機最高速度存在障礙,通常會稱為音障 。事實上,超音速飛行的障礙只有當時尚不成熟的技術。當氣流接近聲速時,常規翼型的阻力係數顯着增加,在當代很難克服高馬赫數產生的大阻力,因此「音障」此一概念於焉誕生。好在飛機設計最終大幅進步,可以生產出Bell X-1 。由查克·葉格(Chuck Yeager)駕駛的X-1於1947年10月正式實現了超音速。 [3]
縱觀歷史,科學家們研究氣體動力學的進程中,分成兩條平行的路徑。實驗氣體動力學,進行風洞模型實驗以及在震波管和彈道實驗,並使用光學影像技術記錄新的發現。理論氣體動力學,則以理論分析應用於可變密度氣體的運動方程式及其解。許多基本的氣體動力學是解析性的,意即一般人可用公式算得解析解,但是在現代,計算流體動力學(Computational Fluid Dynamics)應用電腦計算來解決特定幾何形狀和可壓縮流間,原本棘手的非線性偏微分方程,即所謂數值解。
基本概念
[編輯]
可壓縮流的基礎理論涉及幾個重要的假設:
- 連續性:所有流體都是由分子組成的,但是不必跟着氣流(例如在大氣壓下)中大量的分子單體。藉由假設氣流連續,我們可以將氣流視為低密度的連續物質。只有在高層大氣、太空等低密度的領域中,單一分子的運動才變得重要。
- 無滑動條件:假定固體表面的流速等於表面本身的速度,這是假設連續流動的直接結果。無滑動條件意味着流動具有粘性,而也意味着空氣的高速流動,會在物體上形成邊界層。
不可壓縮流問題大多僅涉及兩個未知數:壓力和速度,通常僅須透過兩個方程式即可求得,方程式描述了質量守恆和線性動量守恆,且流體密度假定為常數。但是,在可壓縮流中,氣體密度和溫度也成為變量。為了解決可壓縮流問題,這需要兩個以上的方程:氣體的狀態方程和能量守恆方程。對於大多數氣體動力學問題,理想氣體是合理且適當的狀態假設。
流體力學問題有兩種做法:拉格朗日法和歐拉法。拉格朗日法在流過流場時遵循特定一塊流體質量。反之,歐拉法則不會隨流體一起移動,而是固定觀察流體流過的同一塊框架或控制體積。雖然拉格朗日法才能看出一個流體如何從前面這樣變成後面那樣,然而實務上不太可能做到這件事,因此做實驗通常採用歐拉法來觀察。
最後,儘管已知空間具有3個維度,但是如果僅其中一維具有最重要的意義,則在數學上描述氣流時可以進行重要的簡化:假定為單維流動。這在計算管路、噴嘴和擴散器的流動時非常有用,因為在這些流動中,流動特性主要只在軸向而非側向上改變。但是計算高速運動物體上的外部流時,至少需要看成二維。當三個空間維度(也許還有時間維度)都很重要時,大概就要求助電腦來算了。
馬赫數,波動和聲速
[編輯]馬赫數(M)定義為速度與聲速之比。例如,在室溫下,聲音經由空氣傳播的速度約為340 m/s(1,100 ft/s) 。 M值的範圍可以從0到∞,但是這種寬泛的範圍又可細分為:亞音速、穿音速、超音速、超高音速和超高速流。下圖是馬赫數光譜,可看到他們如何分佈。
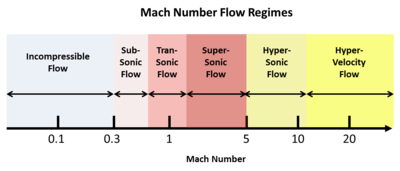
對於馬赫數分類不是隨便找個速度就分的,而是從實驗、理論中發現,在跨越那個馬赫數後,某些特性會變得相當明顯。在流速非常慢時,由於音速快上許多,馬赫數就變得無關緊要,數學上可將其忽略。但是,一旦流動速度接近音速,馬赫數就變得非常重要,並且開始出現震波。因此,穿音速狀態是通過不同的(且更為複雜的)數學來描述。在超音速狀態下,流動以帶有斜角的波運動為主,類似於馬赫角。在大約5馬赫以上時,這些波角變得很小,以至於需要使用不同的數學方法來定義超高音速狀態。最後,從軌道進入行星大氣層時,速度達到數公里/秒,音速現在已經相當慢,以至於在超高速狀態下它在數學上又被忽略了。
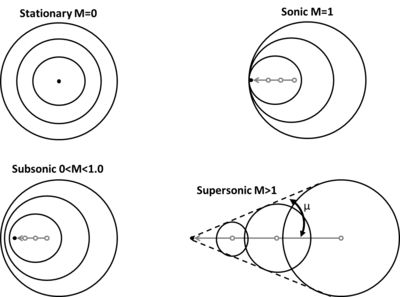
當物體在氣體中從亞音速加速到超音速時,會發生不同類型的波動現象。為了說明這些變化,下圖顯示了一個發出對稱聲波的固定點(M = 0)。在均勻的流體中,聲速在所有方向上都是相同的,因此這些波只是同心球體。隨着發聲點開始加速,聲波在運動方向上「靠攏」,而在相反方向上「遠離」。當該點達到音速(M = 1)時,它與其產生的聲波以相同速度傳播。因此,無限數量的這些聲波在該點之前「堆積」,從而形成震波。在達到超音速流動後,粒子運動得如此之快,以至於它不斷地將聲波留在後面。發生這種情況時,這些點後面的波的軌跡會產生一個稱為馬赫波角或馬赫角μ的角度:
其中代表氣體中聲音的速度, 代表物體的速度。儘管這些斜波以奧地利物理學家恩斯特•馬赫的名字命名,但最早是由克里斯汀多普勒發現。 [4]
單維流動
[編輯]單維(1-D)流是指通過管道或通道的氣流,假定其中的流量參數僅沿一個空間維度(即管道長度)顯着變化。在分析一維通道流時,進行了許多假設:
- 管路長度與寬度之比(L/D)≤約5(以忽略摩擦和傳熱),
- 穩定流vs.不穩定流,
- 流動是等熵的(即可逆且絕熱的過程),
- 理想氣體定律(即P =ρRT)
德拉瓦噴嘴
[編輯]隨着流速從亞音速加速到超音速狀態,氣流經過噴嘴和擴散器的物理特性發生了變化。利用流體動力學和熱力學的守恆定律,建立了以下與通道流動的關係(質量守恆和動量守恆相結合):
- ,
其中dP是壓力的微小變化,M是馬赫數,ρ是氣體密度,V是流速,A是管道截面積,dA是管道面積的微小變化。從方程式中可以知道,對於亞音速流,收縮管道(dA<0)會增加流速,而擴張管道(dA>0)會降低流速。
但當氣流超過音速時,因為(1- M 2)成為負值,讓流動現象相反。現在,收縮管道(dA<0)會降低流速,而擴張管道(dA>0)會提高流速。在Mach = 1時,會發生特殊情況,其中管路截面積必須為最大或最小。實務上,只有讓1馬赫發生在管路的最小截面積,才可以在前方加速、後方繼續達到更高的流速。
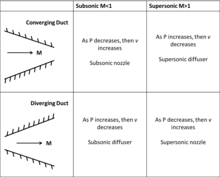
因此,為了將氣流加速到1馬赫,必須將噴嘴設計為收縮到最小截面積,然後擴張。在古斯塔夫·德拉瓦古斯塔夫·德拉瓦發明了這種噴嘴之後,這種類型的噴嘴(收縮噴嘴)會稱為德拉瓦噴嘴。
當亞音速流進入收縮管道且面積減小時,氣流加速。到達管道的最小面積(也稱為噴喉)後,流速必須達到1馬赫。如果要繼續提高流速,則必須降低其密度,以遵守質量守恆原則。為了讓密度降低,氣流必須膨脹。

氣體可達到的最大速度
[編輯]最終,由於能量守恆,氣體基於其能量含量會限制在某個最大速度。氣體可以達到的最大速度V max為:
其中c p是氣體的定壓比熱,T t是氣流停滯溫度。
等熵流馬赫數關係
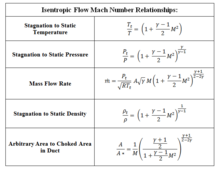
[編輯]利用前述的守恆定律和熱力學,建立了多種形式的關係
其中M是馬赫數,γ是比熱之比(空氣可直接假定為1.4)。
達到超音速
[編輯]如先前所述,為了使氣流超音速,它必須通過管路面積最小處或噴喉。此外,要達到1馬赫,壓力與全壓的比值P b / P t大約為2。一旦達到1馬赫,噴喉處的流速就會阻塞。因為下游的變化只能以音速向上游移動,所以在流量阻塞後,通過噴嘴的質量流動不會受到下游條件變化的影響。
氣體的非等熵單維通道流-正震波
[編輯]正震波是垂直於局部流動方向的震波。
這些震波在壓力波累積並聚集成極薄的震波時產生,該震波將動能轉換為熱能。因此,這些波會相互抵消,也可能相互增強,於是從一系列無限小聲波中形成單一個震波。由於跨越震波的狀態變化高度不可逆,因此震波會造成的熵大量增加。當分析正震波時,運用理想氣體、單維、穩定和絕熱流動等假設。停滯溫度和停滯焓在震波上游和下游相同。
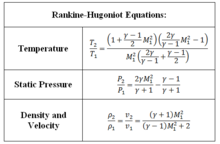
可以定點正震波或移動正震波中任何一個來輕鬆分析正震波。正震波之前的流動必須是超音速的,而正震波之後的流動必須是亞音速的。 Rankine-Hugoniot方程用於求解流動條件。
二維流
[編輯]一維流只是二維流的一種特殊情況。因此,一維流動的定義現象之一,即正震波,同樣只是斜震波中的特例。斜震波在以下應用中更為常見:飛機進氣口設計、超音速飛行以及超音速噴嘴和擴散器。根據流動條件,斜震波可以以艏震波的形式附着在流體上、或從流體上脫離。
 |
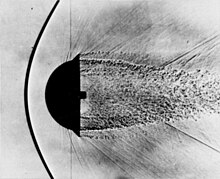 |
斜震波
[編輯]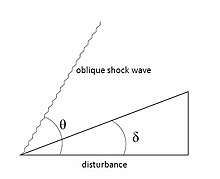
斜震波與正震波相似,但它與流動方向的夾角小於90°。當障礙物以一個不為零的角度(δ)進入流場中時,流場必須響應變化的邊界條件。因此,形成斜震波,導致流動方向的改變。
震波極座標圖
[編輯]
根據流場偏轉的程度(δ),斜震波又分為強或弱。強斜震波的特點是更大的角度和整個震盪的熵損失,而弱斜震波則相反。為了粗略地了解這些震波的差異,可以使用震波極座標圖。震波後的靜溫T *,即震波後的聲速定義為:
其中R為氣體常數,γ為比熱比。馬赫數可以分解為卡氏坐標
用V x和V y作為流體速度V的x和y分量。藉由給出震波前的馬赫數,可以指定條件的軌跡。在一些δmax從強斜震波過渡到弱斜震波。當δ= 0°時,在強斜震波的極限處會產生正震波,而在弱斜震波的極限處會產生馬赫波。
斜震波反射
[編輯]由于震波的傾斜,在產生斜震波後,它可以三種方式與邊界相互作用,下面將對兩種方式進行說明。
固體邊界
[編輯]首先使流場旋轉角度δ,該震波從固體邊界反射,並且流動由–δ轉向,再次與邊界平行。重要的是要注意,每個過程產生的斜震波都更加弱,並且波角會逐漸增加。
不規則反射
[編輯]不規則反射與上述情況非常相似,但要注意的是δ大於最大允許轉向角。因此,形成了分離的震波並且發生了更複雜的反射。
普朗托–邁耶扇
[編輯]普朗托–邁耶扇可以分為壓縮扇和擴張扇。 普朗托–邁耶擴張扇能夠跨越邊界層(即流體和固體),該邊界層也以不同的變化做出反應。當震波打在固體表面時,所得扇將作為對面類型的扇返回,而當擊中自由邊界時,扇將作為對面類型的扇返回。
普朗托–邁耶擴張扇
[編輯]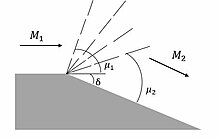
在普朗托和邁耶提出理論以前,唯一會討論到的流體現象是震波,它會減慢流動並增加其熵。而此後,人們才知道普朗托-邁耶膨脹扇現象,是另一個造成超音速流動的可能。
與流場遇到傾斜的障礙物並形成斜震波相反,流體流經凸角擴展並透過一系列等熵馬赫波形成膨脹扇。擴張「扇」由從初始馬赫角到最終馬赫角的馬赫波組成。由於馬赫數的增加僅與通道的凸角(δ)成比例,因此流體可以圍繞尖角或圓角均勻擴張。產生普朗托 - 邁耶扇的擴展角可以是尖銳的(如圖所示)或圓形的。如果總轉向角度相同,則普朗托 - 邁耶扇之解也將相同。
普朗托 - 邁耶擴張可以看作是德拉瓦噴嘴操作的物理解釋。噴嘴的輪廓產生了一系列平滑且連續的普朗托 - 邁耶擴張波。
普朗托 - 邁耶壓縮扇
[編輯]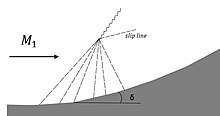
普朗托 - 邁耶壓縮是與擴張相反的現象。
如果將氣流逐漸轉過δ角,則可以形成壓縮扇。該扇也是一系列馬赫波,最終會合併為斜震波。因為流場是由等熵區域(經過扇的流場)和等熵區域(通過斜震波的流場)所定義,故在兩個流動區域之間會產生一條滑移線。
應用
[編輯]超音速風洞
[編輯]超音速風洞用於測試和研究超音速流,大約在1.2至5的馬赫數範圍內。風洞背後的工作原理是在上游到下游保持極大壓差,從而驅動氣流。
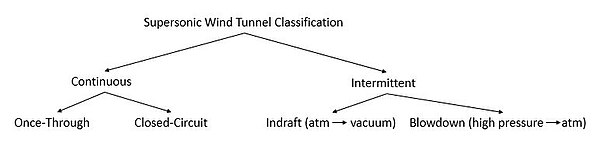
風洞可分為兩類:連續運行和間歇運行的風洞。
連續運行的超音速風洞需要一個獨立的電力來源,隨着測試部分的尺寸越來越大,需要的電源會急劇增加。間歇性超音速風洞的價格較低,因為它們可以在很長的時間裏慢慢存儲電能,然後在簡短的測試中一次釋放。兩者之間的差異就像電池和電容器。
 |
 |
吹放式超音速風洞具有較高的雷諾數,較小的儲氣罐和隨時可用的乾燥空氣。但是它們的高壓可能造成危險,導致難以保持恆定的停滯壓力,並且在操作過程中會產生較大噪音。
吸入式超音速風洞與壓力隱患無關,允許恆定的停滯壓力,並且相對安靜。不幸的是,它們的雷諾數範圍有限,並且需要大型真空儲存槽。
毫無疑問,知識是藉由在超音速風洞中進行研究和測試而獲得;然而,這些設施通常需要大量的電力,來維持測試條件所需的高壓力比。例如,阿諾德工程發展中心擁有世界上最大的超音速風洞,卻需要足以照明一座小城市的電力才得以運行。因此,大型風洞在大學中變得不那麼普遍了。
超音速飛機進氣道
[編輯]斜震波最常見的需求是在超音速飛機的進氣口設計,其速度大於2馬赫(F-16的最大速度為2馬赫,但不需要斜震波進氣)。進氣口的目的之一是使進入的超音速空氣在進入渦輪噴射引擎之前減速至亞音速,從而最大程度地減少震波損失。這是通過以下一種或多種斜震波來完成的,最後是非常弱的正震波,上游馬赫數通常小於1.4。通過進氣道的氣流必須在從最大音速到零,這樣極大的速度範圍內被正確管理。這需要改變進氣道表面的位置來完成。
進氣口的幾何形狀必須要可以變化才能應付從起飛到超過2馬赫的速度,例如,對於約3馬赫的最大速度, XB-70使用具有可調節斜度的矩形入口,而SR-71使用具有可調節中心錐度的圓形入口。

 |
參見
[編輯]參考資料
[編輯]- ^ Anderson, J.D., Fundamentals of Aerodynamics, 4th Ed., McGraw–Hill, 2007.
- ^ 2.0 2.1 Genick Bar–Meir. Fundamentals of Compressible Fluid Mechanics (PDF). ibiblio (Potto Project). May 21, 2007 [January 23, 2020]. (原始內容存檔 (PDF)於2020-01-14).>
- ^ Jr., John D. Anderson. Research in Supersonic Flight and the Breaking of the Sound Barrier. history.nasa.gov. [14 April 2018]. (原始內容存檔於2017-12-25).
- ^ P. M. Schuster:Moving the Stars: Christian Doppler - His Life, His Works and Principle and the World After, Pollauberg, Austria:Living Edition Publishers, 2005
- Liepmann, Hans W.; Roshko, A. Elements of Gasdynamics. Dover Publications. 1957 [1957]. ISBN 0-486-41963-0.
- Anderson, John D. Jr. Modern Compressible Flow 3rd. McGraw-Hill Science/Engineering/Math. 2003 [1982]. ISBN 0-07-242443-5.
- John, James E.; Keith, T. G. Gas Dynamics 3rd. Prentice Hall. 2006 [1969]. ISBN 0-13-120668-0.
- Oosthuizen, Patrick H.; Carscallen, W. E. Introduction to Compressible Flow 2nd. CRC Press. 2013 [1997]. ISBN 978-1439877913.
- Zucker, Robert D.; Biblarz, O. Fundamentals of Gas Dynamics 2nd. Wiley. 2002 [1977]. ISBN 0471059676.
- Shapiro, Ascher H. The Dynamics and Thermodynamics of Compressible Fluid Flow, Volume 1. Ronald Press Company. 1953. ISBN 978-0-471-06691-0.
- Anderson, John D. Jr. Hypersonic and High Temperature Gas Dynamics. AIAA. 2000 [1989]. ISBN 1-56347-459-X.








