在同調代數 中,譜序列 是一種藉着逐步逼近以計算同調或上同調群的技術,由讓·勒雷 在1946年首創。其應用見諸代數拓撲 、群上同調 與同倫理論 。
讓·勒雷當初為了研究代數拓撲學,而引入層 的概念,從而面臨計算層上同調 的問題。為此,勒雷發明了現稱勒雷譜序列 的計算方法,它聯繫了一個層的上同調群與其正像的上同調群。
人們很快就發現:勒雷譜序列只是一個特例。譜序列還現身於纖維化 等幾何問題;更抽象地說,對合成函子取導函子 也會得到譜序列,稱為格羅滕迪克譜序列 。雖然導範疇 在理論層面提供了較簡鍊的框架,譜序列仍是最有效的計算工具。
由於譜序列包含大量的項,實際計算時往往會陷入帶(至少)三重指標的群 或模 的迷陣。在許多實際狀況中,譜序列最後會「塌陷」,此時譜序列可以給出明確的資訊。若譜序列不塌陷,則須靠一些竅門取得有用的資訊。
以下固定一個阿貝爾範疇
A
{\displaystyle {\mathcal {A}}}
模 範疇。譜序列 是一個非負整數
r
0
{\displaystyle r_{0}}
對所有整數
r
≥
r
0
{\displaystyle r\geq r_{0}}
E
r
{\displaystyle E_{r}}
自同態
d
r
:
E
r
→
E
r
{\displaystyle d_{r}:E_{r}\to E_{r}}
d
r
2
=
0
{\displaystyle d_{r}^{2}=0}
邊界映射 或微分 。
從
E
r
+
1
{\displaystyle E_{r+1}}
H
(
E
r
,
d
r
)
{\displaystyle H(E_{r},d_{r})}
通常省去
E
r
+
1
{\displaystyle E_{r+1}}
H
(
E
r
,
d
r
)
{\displaystyle H(E_{r},d_{r})}
最基本的例子是鏈複形
C
∙
{\displaystyle C_{\bullet }}
d
{\displaystyle d}
r
0
=
0
{\displaystyle r_{0}=0}
E
0
=
C
∙
{\displaystyle E_{0}=C_{\bullet }}
E
1
=
H
(
C
∙
)
{\displaystyle E_{1}=H(C_{\bullet })}
E
1
=
E
2
=
⋯
{\displaystyle E_{1}=E_{2}=\cdots }
E
0
=
C
∙
{\displaystyle E_{0}=C_{\bullet }}
E
r
=
H
(
C
∙
)
(
r
≥
1
)
{\displaystyle E_{r}=H(C_{\bullet })\;(r\geq 1)}
由於只有
r
=
0
{\displaystyle r=0}
較常見的是雙分次模(或層)範疇上的譜序列,表作
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
r
{\displaystyle r}
d
r
:
E
r
→
E
r
{\displaystyle d_{r}:E_{r}\to E_{r}}
(
r
,
−
r
+
1
)
{\displaystyle (r,-r+1)}
E
r
{\displaystyle E_{r}}
d
r
:
E
r
→
E
r
{\displaystyle d^{r}:E_{r}\to E_{r}}
(
−
r
,
r
−
1
)
{\displaystyle (-r,r-1)}
譜序列之間的態射
f
:
E
→
E
′
{\displaystyle f:E\to E'}
f
r
:
E
r
→
E
r
′
{\displaystyle f_{r}:E_{r}\to E_{r}'}
E
r
+
1
≃
H
(
E
r
,
d
r
)
{\displaystyle E_{r+1}\simeq H(E_{r},d_{r})}
交換代數中大部分的譜序列來自鏈複形,而已知構造譜序列最有力的方法是 William Massey 的正合偶 。正合偶在代數拓撲學中很常見,此時對於許多譜序列,正合偶是唯一已知的構造法。事實上,正合偶可以用來構造所有已知的譜序列。
同樣固定一個阿貝爾範疇(通常取一個環上的雙分次模)
A
{\displaystyle {\mathcal {A}}}
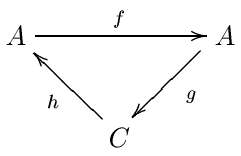
正合偶 是:
一對對象
A
,
C
{\displaystyle A,C}
三個態射:
f
:
A
→
A
{\displaystyle f:A\to A}
g
:
A
→
C
{\displaystyle g:A\to C}
h
:
C
→
A
{\displaystyle h:C\to A}
使之滿足下述正合條件:
Image f = Kernel g
Image g = Kernel h
Image h = Kernel f 將這組資料簡記為
(
A
,
C
,
f
,
g
,
h
)
{\displaystyle (A,C,f,g,h)}
C
{\displaystyle C}
E
0
{\displaystyle E_{0}}
A
{\displaystyle A}
為了得到譜序列的後續項,以下將構造導出偶 。令:
d
:=
g
∘
h
{\displaystyle d:=g\circ h}
A
′
:=
f
(
A
)
{\displaystyle A':=f(A)}
C
′
:=
K
e
r
(
d
)
/
I
m
(
d
)
{\displaystyle C':=\mathrm {Ker} (d)/\mathrm {Im} (d)}
f
′
:=
f
|
A
′
{\displaystyle f':=f|_{A'}}
h
′
:
C
′
→
A
′
{\displaystyle h':C'\to A'}
h
{\displaystyle h}
g
′
:
A
′
→
C
′
{\displaystyle g':A'\to C'}
A
{\displaystyle {\mathcal {A}}}
模 範疇,對任一
a
∈
A
′
{\displaystyle a\in A'}
b
∈
A
′
{\displaystyle b\in A'}
a
=
f
(
b
)
{\displaystyle a=f(b)}
g
′
(
a
)
{\displaystyle g'(a)}
g
(
b
)
{\displaystyle g(b)}
C
′
{\displaystyle C'}
g
′
{\displaystyle g'}
現在可以驗證
(
A
′
,
C
′
,
f
′
,
g
′
,
h
′
)
{\displaystyle (A',C',f',g',h')}
C
′
{\displaystyle C'}
E
1
{\displaystyle E_{1}}
(
A
(
n
)
,
C
(
n
)
,
f
(
n
)
,
g
(
n
)
,
h
(
n
)
)
{\displaystyle (A^{(n)},C^{(n)},f^{(n)},g^{(n)},h^{(n)})}
E
n
:=
C
(
n
)
{\displaystyle E_{n}:=C^{(n)}}
d
n
:=
g
(
n
)
∘
h
(
n
)
{\displaystyle d_{n}:=g^{(n)}\circ h^{(n)}}
譜序列的 E2 項 一個雙分次譜序列含有大量要追蹤的資訊,不過有個常見的圖解法有助於闡明其結構。以下取上同調譜序列為例。在此有三個指標
r
,
p
,
q
{\displaystyle r,p,q}
r
{\displaystyle r}
p
,
q
{\displaystyle p,q}
(
p
,
q
)
{\displaystyle (p,q)}
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
d
r
{\displaystyle d_{r}}
(
r
,
−
r
+
1
)
{\displaystyle (r,-r+1)}
在第一個簡單的例子中,譜序列在
r
≥
1
{\displaystyle r\geq 1}
極限 為
E
∞
:=
E
r
(
r
≥
1
)
{\displaystyle E_{\infty }:=E_{r}\;(r\geq 1)}
定義 :若譜序列
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
(
p
,
q
)
{\displaystyle (p,q)}
r
(
p
,
q
)
∈
N
{\displaystyle r(p,q)\in \mathbb {N} }
r
≥
r
(
p
,
q
)
{\displaystyle r\geq r(p,q)}
d
r
p
−
r
,
q
+
r
−
1
:
E
r
p
−
r
,
q
+
r
−
1
→
E
r
p
,
q
{\displaystyle d_{r}^{p-r,q+r-1}:E_{r}^{p-r,q+r-1}\to E_{r}^{p,q}}
d
r
p
,
q
:
E
r
p
,
q
→
E
r
p
+
r
,
q
−
r
+
1
{\displaystyle d_{r}^{p,q}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1}}
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
極限項 為
E
∞
p
,
q
:=
E
r
p
,
q
{\displaystyle E_{\infty }^{p,q}:=E_{r}^{p,q}}
r
{\displaystyle r}
其中的指標
p
{\displaystyle p}
若存在對象
E
∙
{\displaystyle E^{\bullet }}
⋯
⊂
F
p
+
1
E
∙
⊂
F
p
E
∙
⊂
⋯
{\displaystyle \cdots \subset F^{p+1}E^{\bullet }\subset F^{p}E^{\bullet }\subset \cdots }
β
p
,
q
:
E
∞
p
,
q
≃
g
r
p
E
p
+
q
{\displaystyle \beta ^{p,q}:E_{\infty }^{p,q}\simeq \mathrm {gr} ^{p}E^{p+q}}
⋂
p
F
p
E
∙
=
(
0
)
,
⋃
p
F
p
E
∙
=
E
∙
{\displaystyle \bigcap _{p}F^{p}E^{\bullet }=(0),\bigcup _{p}F^{p}E^{\bullet }=E^{\bullet }}
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
收斂 到
E
∙
{\displaystyle E^{\bullet }}
E
r
p
,
q
⇒
p
E
∞
p
,
q
{\displaystyle E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{p,q}}
習慣上,人們也常將左式寫成
E
2
p
,
q
{\displaystyle E_{2}^{p,q}}
E
2
p
,
q
{\displaystyle E_{2}^{p,q}}
最簡單的收斂特例是退化 :
定義 :固定
r
∈
N
{\displaystyle r\in \mathbb {N} }
s
≥
r
{\displaystyle s\geq r}
d
s
{\displaystyle d_{s}}
r
{\displaystyle r}
退化性保證了
E
r
≃
E
r
+
1
≃
⋯
{\displaystyle E_{r}\simeq E_{r+1}\simeq \cdots }
E
r
{\displaystyle E_{r}}
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
r
=
2
{\displaystyle r=2}
最常見的譜序列之一來自帶有過濾 結構的對象,通常是鏈複形或上鏈複形。這是一個對象
C
{\displaystyle C}
d
:
C
→
C
{\displaystyle d:C\to C}
d
2
=
0
{\displaystyle d^{2}=0}
C
=
F
0
C
⊃
F
1
C
⊃
⋯
F
n
C
⊃
F
n
+
1
C
=
0
{\displaystyle C=F^{0}C\supset F^{1}C\supset \cdots F^{n}C\supset F^{n+1}C=0}
d
F
p
C
⊂
F
p
C
{\displaystyle dF^{p}C\subset F^{p}C}
同調群上也有相應的過濾
F
p
H
(
C
,
d
)
:=
I
m
(
H
(
F
p
C
,
d
)
→
H
(
C
,
d
)
{\displaystyle F^{p}H(C,d):=\mathrm {Im} (H(F^{p}C,d)\to H(C,d)}
對此,定義相應的分次對象
g
r
F
C
:=
⨁
p
≥
0
F
p
C
/
F
p
+
1
C
{\displaystyle \mathrm {gr} _{F}C:=\bigoplus _{p\geq 0}F^{p}C/F^{p+1}C}
g
r
F
H
(
C
)
:=
⨁
p
≥
0
F
p
H
(
C
)
/
F
p
+
1
H
(
C
)
)
{\displaystyle \mathrm {gr} _{F}H(C):=\bigoplus _{p\geq 0}F^{p}H(C)/F^{p+1}H(C))}
取微分映射為零,可視之為複形。
以下式定義譜序列:
Z
r
p
:=
x
∈
F
p
C
:
d
x
∈
F
p
+
r
C
{\displaystyle Z_{r}^{p}:={x\in F^{p}C:dx\in F^{p+r}C}}
E
r
p
:=
Z
r
p
/
(
d
Z
r
−
1
p
−
r
+
1
+
Z
r
−
1
p
+
1
)
=
Z
r
p
/
(
Z
r
p
∩
(
d
F
p
−
r
+
1
C
+
F
p
+
1
C
)
)
{\displaystyle E_{r}^{p}:=Z_{r}^{p}/(dZ_{r-1}^{p-r+1}+Z_{r-1}^{p+1})=Z_{r}^{p}/(Z_{r}^{p}\cap (dF^{p-r+1}C+F^{p+1}C))}
此時有
E
0
p
=
F
p
C
/
F
p
+
1
C
,
E
1
p
=
H
(
g
r
p
C
)
{\displaystyle E_{0}^{p}=F^{p}C/F^{p+1}C,E_{1}^{p}=H(\mathrm {gr} ^{p}C)}
E
r
p
⇒
E
∞
p
=
g
r
p
H
(
C
)
{\displaystyle E_{r}^{p}\Rightarrow E_{\infty }^{p}=\mathrm {gr} ^{p}H(C)}
通常也寫成
E
r
⇒
H
(
C
)
{\displaystyle E_{r}\Rightarrow H(C)}
取
A
{\displaystyle {\mathcal {A}}}
C
{\displaystyle C}
⋯
→
C
q
→
C
q
+
1
→
⋯
{\displaystyle \cdots \to C^{q}\to C^{q+1}\to \cdots }
d
{\displaystyle d}
p
,
q
,
r
{\displaystyle p,q,r}
E
0
p
,
q
=
F
p
C
p
+
q
/
F
p
+
1
C
p
+
q
{\displaystyle E_{0}^{p,q}=F^{p}C^{p+q}/F^{p+1}C^{p+q}}
E
1
p
,
q
=
H
p
+
q
(
g
r
p
C
∙
)
{\displaystyle E_{1}^{p,q}=H^{p+q}(\mathrm {gr} ^{p}C^{\bullet })}
E
∞
p
,
q
=
g
r
p
(
H
p
+
q
(
C
∙
)
)
{\displaystyle E_{\infty }^{p,q}=\mathrm {gr} ^{p}(H^{p+q}(C^{\bullet }))}
以下考慮取值在某個阿貝爾範疇中的雙複形 ,即一組對象
C
p
,
q
{\displaystyle C^{p,q}}
d
′
:
C
p
,
q
→
C
p
+
1
,
q
{\displaystyle d':C^{p,q}\to C^{p+1,q}}
d
″
:
C
p
,
q
→
C
p
,
q
+
1
{\displaystyle d'':C^{p,q}\to C^{p,q+1}}
d
′
2
=
d
″
2
=
0
{\displaystyle d'^{2}=d''^{2}=0}
d
′
d
″
+
d
″
d
′
=
0
{\displaystyle d'd''+d''d'=0}
對一個雙複形,可定義其全複形
(
C
,
D
)
{\displaystyle (C,D)}
T
(
C
)
{\displaystyle T(C)}
T
o
t
(
C
)
{\displaystyle \mathrm {Tot} (C)}
C
n
:=
⨁
p
+
q
=
n
C
p
,
q
{\displaystyle C^{n}:=\bigoplus _{p+q=n}C^{p,q}}
D
:=
d
′
+
d
″
{\displaystyle D:=d'+d''}
C
{\displaystyle C}
(
′
F
p
C
)
n
:=
⨁
i
+
j
=
n
,
i
≥
p
C
i
,
j
{\displaystyle ('F^{p}C)^{n}:=\bigoplus _{i+j=n,\,i\geq p}C^{i,j}}
(
″
F
q
C
)
n
:=
⨁
i
+
j
=
n
,
j
≥
q
C
i
,
j
{\displaystyle (''F^{q}C)^{n}:=\bigoplus _{i+j=n,\,j\geq q}C^{i,j}}
它們給出兩個譜序列
′
E
r
{\displaystyle 'E_{r}}
″
E
r
{\displaystyle ''E_{r}}
′
E
0
,
′
E
1
,
′
E
2
{\displaystyle 'E_{0},'E_{1},'E_{2}}
′
E
0
i
,
j
=
C
i
,
j
{\displaystyle 'E_{0}^{i,j}=C^{i,j}}
′
E
1
i
,
j
=
H
d
″
j
(
C
i
,
∙
)
{\displaystyle 'E_{1}^{i,j}=H_{d''}^{j}(C^{i,\bullet })}
′
E
2
i
,
j
=
H
d
′
i
(
H
d
″
j
(
C
∙
,
∙
)
)
{\displaystyle 'E_{2}^{i,j}=H_{d'}^{i}(H_{d''}^{j}(C^{\bullet ,\bullet }))\qquad }
同理可計算
″
E
0
,
″
E
1
,
″
E
2
{\displaystyle ''E_{0},''E_{1},''E_{2}}
″
E
0
i
,
j
=
C
j
,
i
{\displaystyle ''E_{0}^{i,j}=C^{j,i}}
″
E
1
i
,
j
=
H
d
′
j
(
C
∙
,
i
)
{\displaystyle ''E_{1}^{i,j}=H_{d'}^{j}(C^{\bullet ,i})}
″
E
2
i
,
j
=
H
d
″
i
(
H
d
′
j
(
C
∙
,
∙
)
)
{\displaystyle ''E_{2}^{i,j}=H_{d''}^{i}(H_{d'}^{j}(C^{\bullet ,\bullet }))\qquad }
這兩個譜序列通常是不同的,但隨着
r
{\displaystyle r}
H
(
C
)
{\displaystyle H(C)}
利用譜序列,可以迅速導出Tor函子 的交換性,即一自然同構:
T
o
r
i
(
M
,
N
)
=
T
o
r
i
(
N
,
M
)
{\displaystyle \mathrm {Tor} _{i}(M,N)=\mathrm {Tor} _{i}(N,M)}
取定平坦分解
P
∙
→
M
→
0
{\displaystyle P_{\bullet }\to M\to 0}
Q
∙
→
N
→
0
{\displaystyle Q_{\bullet }\to N\to 0}
d
,
e
{\displaystyle d,e}
C
i
,
j
:=
P
i
⊗
Q
j
{\displaystyle C_{i,j}:=P_{i}\otimes Q_{j}}
d
i
,
j
:=
d
i
⊗
i
d
+
(
−
1
)
j
i
d
⊗
e
j
{\displaystyle d_{i,j}:=d_{i}\otimes \mathrm {id} +(-1)^{j}\mathrm {id} \otimes e_{j}}
′
E
p
,
q
2
=
H
p
I
(
H
q
I
I
(
P
∙
⊗
Q
∙
)
)
=
H
p
I
(
P
∙
⊗
H
q
I
I
(
Q
∙
)
)
{\displaystyle 'E_{p,q}^{2}=H_{p}^{I}(H_{q}^{II}(P_{\bullet }\otimes Q_{\bullet }))=H_{p}^{I}(P_{\bullet }\otimes H_{q}^{II}(Q_{\bullet }))}
″
E
p
,
q
2
=
H
q
I
I
(
H
p
I
(
P
∙
⊗
Q
∙
)
)
=
H
q
I
I
(
Q
∙
⊗
H
p
I
(
P
∙
)
)
{\displaystyle ''E_{p,q}^{2}=H_{q}^{II}(H_{p}^{I}(P_{\bullet }\otimes Q_{\bullet }))=H_{q}^{II}(Q_{\bullet }\otimes H_{p}^{I}(P_{\bullet }))}
由於複形
P
∙
,
Q
∙
{\displaystyle P_{\bullet },Q_{\bullet }}
H
p
I
(
P
∙
⊗
N
)
=
Tor
p
(
M
,
N
)
{\displaystyle H_{p}^{I}(P_{\bullet }\otimes N)={\mbox{Tor}}_{p}(M,N)}
H
q
I
I
(
Q
∙
⊗
M
)
=
Tor
q
(
N
,
M
)
{\displaystyle H_{q}^{II}(Q_{\bullet }\otimes M)={\mbox{Tor}}_{q}(N,M)}
故
′
E
p
,
q
2
{\displaystyle 'E_{p,q}^{2}}
p
=
0
{\displaystyle p=0}
″
E
p
,
q
2
{\displaystyle ''E_{p,q}^{2}}
q
=
0
{\displaystyle q=0}
Tor
p
(
M
,
N
)
≅
E
p
,
q
∞
=
gr
p
H
p
+
q
(
T
(
C
∙
,
∙
)
)
{\displaystyle {\mbox{Tor}}_{p}(M,N)\cong E_{p,q}^{\infty }={\mbox{gr}}_{p}H^{p+q}(T(C_{\bullet ,\bullet }))}
Tor
q
(
N
,
M
)
≅
E
p
,
q
∞
=
gr
q
H
p
+
q
(
T
(
C
∙
,
∙
)
)
{\displaystyle {\mbox{Tor}}_{q}(N,M)\cong E_{p,q}^{\infty }={\mbox{gr}}_{q}H^{p+q}(T(C_{\bullet ,\bullet }))}
當
p
=
q
{\displaystyle p=q}
運用譜序列時,通常會假設某些項為零,或假設譜序列在第一或第二頁退化。但有時儘管對各項及微分映射一無所知,仍可從譜序列中萃取資訊,最簡單的例子是示性數 :固定一個阿貝爾範疇
A
{\displaystyle {\mathcal {A}}}
C
{\displaystyle C}
χ
:
O
b
A
→
C
{\displaystyle \chi :\mathrm {Ob} {\mathcal {A}}\to C}
∀
0
→
Y
→
X
,
χ
(
X
)
=
χ
(
Y
)
+
χ
(
X
/
Y
)
{\displaystyle \forall 0\to Y\to X,\;\chi (X)=\chi (Y)+\chi (X/Y)}
X
≃
Y
⇒
χ
(
X
)
=
χ
(
Y
)
{\displaystyle X\simeq Y\Rightarrow \chi (X)=\chi (Y)}
例如:取
A
{\displaystyle {\mathcal {A}}}
k
{\displaystyle k}
向量空間 範疇,則
χ
:
V
↦
dim
k
V
{\displaystyle \chi :V\mapsto \dim _{k}V}
對任一
A
{\displaystyle {\mathcal {A}}}
K
∙
{\displaystyle K^{\bullet }}
χ
(
K
∙
)
=
∑
i
(
−
1
)
i
χ
(
K
i
)
{\displaystyle \chi (K^{\bullet })=\sum _{i}(-1)^{i}\chi (K^{i})}
容易證明
χ
(
K
∙
)
=
∑
i
(
−
1
)
i
χ
(
H
i
(
K
∙
)
)
{\displaystyle \chi (K^{\bullet })=\sum _{i}(-1)^{i}\chi (H^{i}(K^{\bullet }))}
A
{\displaystyle {\mathcal {A}}}
(
E
r
∙
)
{\displaystyle (E_{r}^{\bullet })}
χ
(
E
r
∙
)
=
χ
(
E
r
+
1
∙
)
=
⋯
=
χ
(
E
∞
∙
)
{\displaystyle \chi (E_{r}^{\bullet })=\chi (E_{r+1}^{\bullet })=\cdots =\chi (E_{\infty }^{\bullet })}
然而
χ
(
E
n
)
=
∑
p
χ
(
F
p
E
n
/
F
p
+
1
E
n
)
=
∑
p
χ
(
E
∞
p
,
n
−
p
)
{\displaystyle \chi (E^{n})=\sum _{p}\chi (F^{p}E^{n}/F^{p+1}E^{n})=\sum _{p}\chi (E_{\infty }^{p,n-p})}
於是得到
∀
r
,
∑
n
(
−
1
)
n
χ
(
E
n
)
=
χ
(
E
r
∙
)
{\displaystyle \forall r,\;\sum _{n}(-1)^{n}\chi (E^{n})=\chi (E_{r}^{\bullet })}
Leray, Jean. L'anneau d'homologie d'une représentation. C. R. Acad. Sci. Paris. 1946, 222 : 1366––1368. Leray, Jean. Structure de l'anneau d'homologie d'une représentation. C. R. Acad. Sci. Paris. 1946, 222 : 1419––1422. Koszul, Jean-Louis. Sur les opérateurs de dérivation dans un anneau. C. R. Acad. Sci. Paris. 1947, 225 : 217––219. Massey, William S. Exact couples in algebraic topology. I, II. Ann. of Math. (2nd series). 1952, 56 : 363––396. Massey, William S. Exact couples in algebraic topology. III, IV, V. Ann. of Math. (2nd series). 1953, 57 : 248––286. S.N. Malygin, Spectral Sequence , Hazewinkel, Michiel (編), 数学百科全书 , Springer , 2001, ISBN 978-1-55608-010-4 McCleary, John. A User's Guide to Spectral Sequences 2nd Edition. Cambridge University Press. February 2001: 560 pp. doi:10.2277/0521567599 ISBN 978-0-521-56759-6 . Mosher, Robert; Martin Tangora. Cohomology Operations and Applications in Homotopy Theory . Harper and Row. 1968. Hatcher, Allen. Spectral Sequences in Algebraic Topology (PDF) . [2007-08-17 ] . (原始內容存檔 於2014-02-05). Chow, Timothy Y. You Could Have Invented Spectral Sequences (PDF) . Notices of the American Mathematical Society. January 2006, 53 : 15––19 [2007-08-17 ] . (原始內容存檔 (PDF) 於2006-10-06).