梯形菱形十二面体
外观
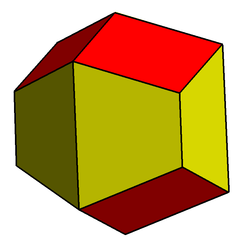 | |||
| 类别 | 约翰逊多面体对偶 | ||
|---|---|---|---|
| 对偶多面体 | 同相双三角台塔 | ||
| 性质 | |||
| 面 | 6 菱形 6 等腰梯形 | ||
| 边 | 24 | ||
| 顶点 | 14 | ||
| 欧拉特征数 | F=12, E=24, V=14 (χ=2) | ||
| 组成与布局 | |||
| 顶点布局 | (2) 4.4.4 (6) 4.4.4.4 (6) 4.4.4 | ||
| 对称性 | |||
| 对称群 | D3h, [3,2], (*322), order 12 | ||
| 旋转对称群 | D3, [3,2]+, (322), order 6 | ||
| 特性 | |||
| 凸 | |||
| 图像 | |||
| |||
在几何学中,梯形菱形十二面体是一种凸十二面体,由六个菱形和六个等腰梯形所组成,并形成三种不同的顶点,其对偶多面体为同相双三角台塔,因此梯形菱形十二面体可以视为经过一次康威变换的约翰逊多面体。
梯形菱形十二面体具有D3h的对称性,并且能独立完成堆砌,即可以完全填充(密铺)整个空间。
结构
[编辑]此多面体可以通过拉高正六角柱,并切割顶部和底部产生三个角而构成。梯形表示原来正六角柱的边,6个菱形则代表顶部和底部的切割结果。
空间填充
[编辑]在三维欧几里得空间中,梯形菱形十二面体可以独立填充空间,形成梯形菱形十二面体堆砌,可利用平移与复制梯形菱形十二面体来构造。每一“层”可以视为正六边形镶嵌或菱形镶嵌,然后交替层通过将它们的中心旋转每个多面体使菱形面搭配起来连接。
参见
[编辑]参考文献
[编辑]- Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979: 170. ISBN 0-486-23729-X.
- 埃里克·韦斯坦因. Space-filling polyhedron. MathWorld.



