杰克逊结构化编程
杰克森结构化程式设计(Jackson structured programming)简称JSP,是一种结构化编程方法,以资料流结构及程序结构之间的对应关系为基础。JSP会将程序及资料用序列(sequence)结构、迭代(iteration)结构及选择(selection)结构的组合来表示,适合用来设计程序的细部控制结构,若是较高层次的控制则会使用面向对象程式设计[1][2]。
简介
[编辑]迈克尔·安东尼·杰克逊在1975年在《Principles of Program Design》一书中提出杰克森结构化程式设计。[3]。杰克森的目的是要使COBOL批处理文件进程更容易更改及维护,但此程式设计方式可用在任何有结构化流程控制的编程语言,例如C语言、Java及Perl。虽然JSP已有很长的历史,不过像微软的Visio及像是Jackson Workbench的电脑辅助软件工程工具仍支持JSP[4]。
JSP中的许多内容和Warnier/Orr图有关[5][6],不过后者专注在输出流的结构。JSP和Warnier/Orr图都将程序及资料由序列、迭代及选择三个结构来表示,基本上创立了正则表达式的语法分析器程序,可同时符合程序输入及输出的资料流。
JSP着重资料流,因此所产生的程序的结构和用其他利用像维尔特或戴克斯特拉的逐步细化方法所产生程序的结构不同。JSP所设计程序的主要特点是在代码中会有多个输入指令,而使用其他逐步细化方法的程序一般只有一个输入指令。杰克森在《Principles of Program Design》的第三章,列出了二个程序以说明不同结构化程式设计的差异[3]。
结构等效的二个程序
[编辑]此程序的JSP版本如下
String line;
line = in.readLine();
while (line != null) {
int count = 0;
String firstLineOfGroup = line;
while (line != null && line.equals(firstLineOfGroup)) {
count++;
line = in.readLine();
}
System.out.println(firstLineOfGroup + " " + count);
}
使用其他结构化设计方式的程序如下
String line;
int count = 0;
String firstLineOfGroup = null;
while ((line = in.readLine()) != null) {
if (firstLineOfGroup == null
|| !line.equals(firstLineOfGroup)) {
if (firstLineOfGroup != null) {
System.out.println(firstLineOfGroup + " " + count);
}
count = 0;
firstLineOfGroup = line;
}
count++;
}
if (firstLineOfGroup != null) {
System.out.println(firstLineOfGroup + " " + count);
}
杰克逊认为使用其他结构化设计方式的程序无法表达输入资料行之间的关系,例如将第一行的处理视为一个特例,最后一行的输出也要用特例来处理,影响程序的可理解性及可维护性。
方法
[编辑]JSP使用半型式化步骤来找出程序输入输出资料的结构,以及程序本身的结构。
其目的是建立在整个生命周期都方便修改的程序。杰克逊主要的见解是需求变更多半是针对现有结构的微小调整,针对用JSP撰写的程序,其输入数据结构、输出数据结构及程序内在结构皆可对应,因此输入及输出的微小变化只会对应为程序的微小变化。
JSP将程序分为四种不同的组件:
- 基本程序
- 序列(sequences)
- 迭代(iterations)
- 选择(selections)
JSP一开始会以上述四个组件来描述程序的输入,随后以类似的方式处理程序的输出,每一个输入及输出都以独立的数据结构图(DSD)来表示。针对一些密集运算的应用(例如数码信号处理),也需要绘制算法结构图,着重在内部资料的结构,而不是输入或输出资料的结构。
输入及输出的结构之后会集成成最终的程序结构,称为程序结构图(PSD)。其中可能包括加入少许的高阶控制结构,集成输入及输出的特性。一部分程序是处理产生输出前的所有输入资料,其他程序则是以循环的方式,先读取资料再输出资料,在产生程序结构图时需找到类似的结构。
随后程序结构图会以编程语言来实现。JSP着重在程序的控制结构,因此实现时只会用到基本程序、序列、迭代及选择。JSP没有使用类别及物件及层次来架构程序,不过使用类别的方法也有助控制流程的结构化。
JSP使用图像的表示法来描述输入、输出及程序的结构。
基本程序会以方块来表示。

一连串的程序会用以直线相连的方块表示,图例中,步骤A之后为步骤B、C、D。

迭代的步骤也是用相连的方块来表示,要迭代的步骤方块右上角会有一个星号。图例中,步骤A包括执行0次或多次的步骤B。
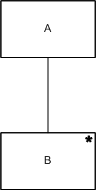
选择的步骤也是用相连的方块来表示,待选择的步骤方块右上角会有一个圆形。图例中,步骤A会选择执行步骤B、C或D中的一个步骤。

实例
[编辑]以下以一个游程编码的程序来说明JSP的设计方式。游程编码是指一个程序的输入是字节的资料流,其输出的资料由字节及此字节连续出现的次数所组成,游程编码常用在位图的压缩。
利用JSP设计程序,首先是描述程序输入的结构,游程编码只有一种输入,是由零个或多个“游程”所组成的资料流,每个“游程”为一个字节,或是多个相同数值的字节,上述结构可以用以下的JSP图表示:

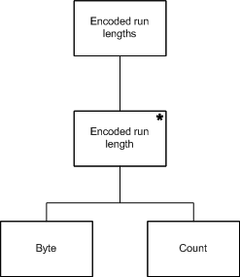
第二步则是描述程序输出的结构,游程编码的输出可视为零到多对资料的资料流,每一对数据包括一个字节和其出现的次数,在此例中,次数也用字节来表示:

下一个步骤是描述输入结构及输出结构之间程序的相关性:
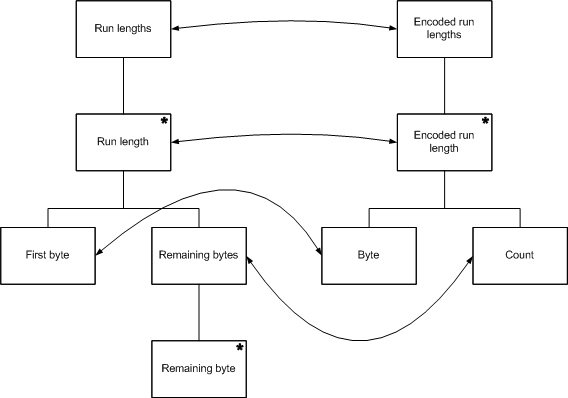
有时程式设计者在此阶段会遇到结构冲突的问题,也就是输入及输出结构之间没有明显的关系。若出现结构冲突的问题,可以将程序分为二部分,二部分程序之间有共通的资料,二部分的程序可以用共通的资料作为共同的控制框架,这二部分程序常常会用行程或协程的方式来实现。
此例没有结构冲突的问题,因此二个数据结构可以合并为以下的程序结构:
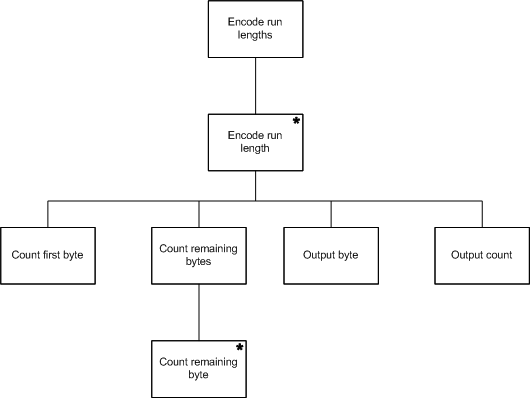
此时程序可以加入对应的基本程序来充实其内容,基本程序如下:
- 读一个字节
- 记录一个字节
- 设置计数器为零
- 计数器递增
- 输出记录的字节
- 输出计数器
也需要找到程序中迭代的部分,迭代的部分如下:
- 当还有字节时
- 当还有字节、字节和记录的字节相同、而且计数器数值仍可以用字节表示时
若集成上述所有的资料,可以将图和基本程序以C语言来表示,并且在代码、动作及程式设计图的结构之间建立一对一的对应关系。
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[])
{
char c;
c = getchar();
while (c != EOF) {
char count = 1;
char first_byte = c;
c = getchar();
while (c != EOF && c == first_byte && count < 255) {
count++;
c = getchar();
}
putchar(first_byte);
putchar(count);
}
return EXIT_SUCCESS;
}
相关条目
[编辑]参考资料
[编辑]- ^ R. Wieringa (1998). "A survey of structured and object-oriented software specification methods and techniques". in: ACM Comput. Surv. 30, 4 (Dec. 1998), 459-527. DOI= http://doi.acm.org/10.1145/299917.299919
- ^ Brian Henderson-Sellers and J.M. Edwards (1990). "The object-oriented systems life cycle". In: Commun. ACM 33, 9 (Sep. 1990), 142-159. DOI= http://doi.acm.org/10.1145/83880.84529
- ^ 3.0 3.1 M.A. Jackson (1975). Principles of Program Design. Academic Press. 1975
- ^ Nicholas Ourusoff. Using Jackson Structured Programming (JSP) and Jackson Workbench to Teach Program Design (PDF). InSite 2003. Informing Science. 2003 [2008-02-18]. (原始内容 (pdf)存档于2011-07-26).
- ^ K.T. Orr (1980). "Structured programming in the 1980s". In: Proceedings of the ACM 1980 Annual Conference ACM '80. ACM Press, New York, NY, 323-326. DOI= http://doi.acm.org/10.1145/800176.809987
- ^ J.D. Warnier (1974). Logical Construction of Programs. Van Nostrand Reinhold, N.Y., 1974
