單態射

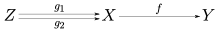
在範疇論裡，一個態射被稱之為單態射，則該態射為一具左消去律的態射。亦即，給定一單態射 $f:X\rightarrow Y$，則對所有的態射$g_{1},g_{2}:Z\rightarrow X$，均能使得

$f\circ g_{1}=f\circ g_{2}\Rightarrow g_{1}=g_{2}.$

單態射是單射函數（或稱為一對一函數）在範畤論裡的延伸。單態射的對偶概念為滿態射，後者為滿射函數的延伸。一態射於範疇 $C$ 裡為單態射，則該態射於對偶範疇 $C^{op}$ 裡為滿態射。

性質

• 具左反元素的態射必為一單態射。因為，如一態射 $f$ 具有一左反元素 $l$（即 $l$ 為一態射，且$l\circ f=\operatorname {id} _{X}$），則可知

$f\circ g_{1}=f\circ g_{2}\Rightarrow l\circ f\circ g_{1}=l\circ f\circ g_{2}\Rightarrow g_{1}=g_{2}.$

• 不是每一個單態射都會有左反元素。舉例來說，在由所有群所組成的範疇Group裡，如 $H$ 是 $G$ 的子群，則其包含映射 $f:H\rightarrow G$ 總會是個單態射；但 $f$ 於該範疇裡具有一左反元素，若且唯若 $H$ 在 $G$ 裡有一正規補群。

• 如態射 $f$ 的左反元素為一態射 $l$ ，則態射 $f$ 為態射 $l$ 的右反元素，並稱 $f$ 為 $l$ 的截面，$l$ 為f 的收縮。每個截面都會是個單態射，且每個收縮都會是個滿態射。

• 一態射 $f:X\rightarrow Y$ 為單態射，若且唯若對所有的 $Z$，定義一個映射 $f_{*}:\hom(Z,X)\rightarrow \hom(Z,Y)$， 使得對所有的態射$h:Z\rightarrow X$，$f_{*}(h)=f\circ h$，則其映射必為單射。

• 在具體範疇裡，每個為單射函數的態射均為單態射；換句話說，當態射實際上為集合間的函數時，一態射如為一對一函數，則該態射必為單態射。

• 在集合範疇裡，每個單態射也會是個單射態射。該敘述在大多數可於代數裡自然產生的範疇裡也都成立，如在由所有群組成的範疇、由所有環組成的範疇，及所有的阿貝爾範疇裡，每個單態射都會是個單射態射。

• 不是在所有的具體範疇裡，每個單態射都會是個單射態射。舉例來說，在由可除交換群所組成的範疇裡，其中即存在著為單態射，但不為單射態射的群同態，如商映射$q:\mathbb {Q} \rightarrow \mathbb {Q} /\mathbb {Z}$（其中的 $\mathbb {Q}$ 為由有理數在加法運算下所組成的群，$\mathbb {Z}$ 為由整數在加法運算下所組成的群，且 $\mathbb {Q} /\mathbb {Z}$ 為其商群)不是單射（因為每個整數都會映射至0），但為單態射。

另見

• 嵌入 (數學)
• 子對象

參考資料

• George Bergman (1998), An Invitation to General Algebra and Universal Constructions（頁面存檔備份，存於網際網路檔案館）, Henry Helson Publisher, Berkeley. ISBN 0-9655211-4-1.
• Francis Borceux (1994), Handbook of Categorical Algebra 1, Cambridge University Press. ISBN 0-521-44178-1.
• Monomorphism, 数学百科全书, EMS Press, 2001 （英語） 
• Jaap van Oosten, Basic Category Theory（頁面存檔備份，存於網際網路檔案館）