高级加密标准
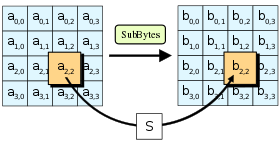 SubBytes是AES演算法四步驟之一。 | |
| 概述 | |
|---|---|
| 设计者 | Vincent Rijmen、Joan Daemen |
| 首次发布 | 1998年 |
| 衍生自 | Square |
| 继承算法 | Anubis、Grand Cru、Kalyna |
| 密码细节 | |
| 密钥长度 | 128、192或者256位元[a] |
| 分组长度 | 128位元[b] |
| 结构 | 置換排列網絡 |
| 重复回数 | 10, 12或14(視密鑰長度而定) |
| 最佳公开破解 | |
| 關聯密碼攻擊可以破解9個加密迴圈/256位元(密鑰)的AES。另外選擇明文攻擊可以破解8個加密迴圈,192或256位元(密鑰)的AES,或7個加密迴圈、128位元(密鑰)的AES。(Ferguson et al., 2000) | |
進階加密标准(英語:Advanced Encryption Standard,缩写:AES),又称Rijndael加密法(荷兰语发音:[ˈrɛindaːl],音似英文的「Rhine doll」),是美国联邦政府采用的一種區塊加密标准。这个标准用来替代原先的DES,已經被多方分析且廣為全世界所使用。經過五年的甄選流程,進階加密標準由美國國家標準與技術研究院(NIST)於2001年11月26日發佈於FIPS PUB 197,並在2002年5月26日成為有效的標準。現在,進階加密标准已然成為对称密钥加密中最流行的演算法之一。
该演算法為比利时密码学家Joan Daemen和Vincent Rijmen所設計,結合兩位作者的名字,以Rijndael為名投稿進階加密標準的甄選流程。
沿革[编辑]
Rijndael是由Daemen和Rijmen早期所设计的Square改良而來;而Square則是由SHARK发展而来。
不同於它的前任標準DES,Rijndael使用的是代换-置换网络,而非Feistel架構。
密码说明[编辑]
严格地说,AES和Rijndael加密法並不完全一樣(虽然在实际应用中兩者可以互换),因为Rijndael加密法可以支援更大範圍的區塊和密钥长度:AES的區塊長度固定為128位元,密钥长度則可以是128,192或256位元;而Rijndael使用的密钥和區塊长度均可以是128,192或256位元。加密過程中使用的密钥是由Rijndael密钥生成方案產生。
大多数AES计算是在一个特别的有限域完成的。
AES加密過程是在一個4×4的位元組矩陣上運作,這個矩陣又称为「体(state)」,其初值就是一個明文區塊(矩陣中一個元素大小就是明文區塊中的一個Byte)。(Rijndael加密法因支援更大的區塊,其矩陣的「列數(Row number)」可視情況增加)加密时,各轮AES加密迴圈(除最后一轮外)均包含4个步骤:
- AddRoundKey—矩陣中的每一个位元組都与該次回合金鑰(round key)做XOR運算;每个子密钥由密钥生成方案产生。
- SubBytes—透過一个非线性的替換函數,用查找表的方式把每个字節替換成對應的字節。
- ShiftRows—將矩陣中的每個橫列進行循環式移位。
- MixColumns—為了充分混合矩陣中各個直行的操作。這個步驟使用線性轉換來混合每行內的四個字节。最後一個加密迴圈中省略MixColumns步驟,而以另一個AddRoundKey取代。
AddRoundKey步骤[编辑]
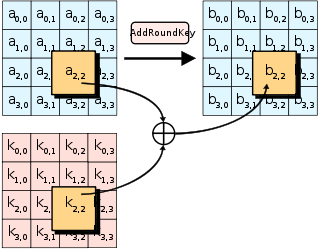
AddRoundKey步驟,回合金鑰將會與原矩陣合併。在每次的加密迴圈中,都會由主密鑰產生一把回合金鑰(透過Rijndael密鑰生成方案產生),這把金鑰大小會跟原矩陣一樣,以與原矩陣中每個對應的位元組作异或(⊕)加法。
SubBytes步骤[编辑]
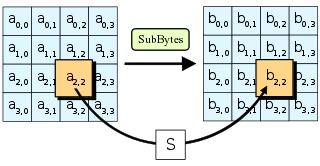
在SubBytes步骤中,矩陣中的各字節透過一個8位元的S-box進行轉換。這個步驟提供了加密法非線性的變換能力。S-box與上的乘法反元素有關,已知具有良好的非線性特性。為了避免簡單代數性質的攻擊,S-box結合了乘法反元素及一個可逆的仿射變換矩陣建構而成。此外在建構S-box時,刻意避開了不動點與反不動點,即以S-box替換字節的結果會相當於錯排的結果。Rijndael S-box條目有針對S-box的詳細描述。
ShiftRows步骤[编辑]
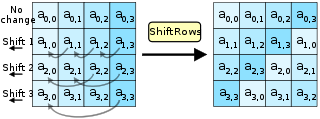
ShiftRows描述矩陣的行操作。在此步驟中,每一行都向左循環位移某個偏移量。在AES中(區塊大小128位元),第一行維持不變,第二行裡的每個位元組都向左循環移動一格。同理,第三行及第四行向左循環位移的偏移量就分別是2和3。128位元和192位元的區塊在此步驟的循環位移的模式相同。經過ShiftRows之後,矩陣中每一竖列,都是由輸入矩陣中的每個不同列中的元素組成。Rijndael演算法的版本中,偏移量和AES有少許不同;對於長度256位元的區塊,第一行仍然維持不變,第二行、第三行、第四行的偏移量分別是1位元組、2位元組、3位元組。除此之外,ShiftRows操作步驟在Rijndael和AES中完全相同。
MixColumns步骤[编辑]
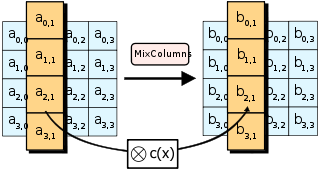
在MixColumns步骤,每一列的四個位元組透過线性变换互相結合。每一列的四個元素分別當作的係數,合併即為中的一個多項式,接著將此多項式和一個固定的多項式在模下相乘。此步驟亦可視為Rijndael有限域之下的矩陣乘法。MixColumns函数接受4個位元組的輸入,輸出4個位元組,每一個輸入的位元組都會對輸出的四個位元組造成影響。因此ShiftRows和MixColumns兩步驟為這個密碼系統提供了擴散性。
以下條目有對MixColumns更加詳細的描述:Rijndael mix columns
加密演算法优化[编辑]
使用32或更多位元定址的系統,可以事先對所有可能的輸入建立對應表,利用查表來實作SubBytes,ShiftRows和MixColumns步驟以達到加速的效果。這麼作需要產生4個表,每個表都有256個格子,一個格子記載32位元的輸出;約佔去4KB(4096位元組)記憶體空間,即每個表佔去1KB的記憶體空間。如此一來,在每個加密迴圈中,只需要查16次表,作12次32位元的XOR運算,以及AddRoundKey步驟中4次32位元XOR運算。若使用的平台記憶體空間不足4KB,也可以利用循環交換的方式一次查一個256格32位元的表。
然而,實際實作中應避免使用這樣的對應表,否則可能因為產生快取命中與否的差別而使旁道攻擊成為可能。
安全性[编辑]
截至2006年,针对AES唯一的成功攻击是旁道攻击或社會工程學攻擊。美国国家安全局审核了所有的參與競選AES的最終入圍者(包括Rijndael),认为他們均能夠满足美国政府傳遞非機密文件的安全需要。2003年6月,美国政府宣布AES可以用于加密机密文件:
The design and strength of all key lengths of the AES algorithm(i.e., 128, 192 and 256)are sufficient to protect classified information up to the SECRET level. TOP SECRET information will require use of either the 192 or 256 key lengths. The implementation of AES in products intended to protect national security systems and/or information must be reviewed and certified by NSA prior to their acquisition and use.[1]
(譯:AES加密演算法(使用128,192,和256位元密鑰的版本)的安全性,在設計結構及密鑰的長度上俱已到達保護機密資訊的標準。最高機密資訊的傳遞,則至少需要192或256位元的密鑰長度。用以傳遞國家安全資訊的AES實作產品,必須先由國家安全局審核認證,方能被發放使用。)
这标志着,由美国国家安全局NSA批准在最高机密資訊上使用的加密系統首次可以被公開使用。许多大众化产品只使用128位元密鑰當作預設值;由於最高機密文件的加密系統必須保證數十年以上的安全性,故推測NSA可能認為128位元太短,才以更長的密鑰長度為最高機密的加密保留了安全空間。
通常破解一個區塊加密系統最常見的方式,是先對其較弱版本(加密迴圈次數較少)嘗試各種攻擊。AES中128位元密鑰版本有10個加密迴圈,192位元密鑰版本有12個加密迴圈,256位元密鑰版本則有14個加密迴圈。至2006年為止,最著名的攻擊是針對AES 7次加密迴圈的128位元密鑰版本,8次加密迴圈的192位元密鑰版本,和9次加密迴圈的256位元密鑰版本所作的攻擊。[2]
由於已遭破解的弱版的AES,其加密迴圈數和原本的加密迴圈數相差無幾,有些密碼學家開始擔心AES的安全性:要是有人能將該著名的攻擊加以改進,這個區塊加密系統就會被破解。在密碼學的意義上,只要存在一個方法,比窮舉法還要更有效率,就能被視為一種「破解」。故一個針對AES 128位元密鑰的攻擊若「只」需要2120計算複雜度(少於窮舉法2128),128位元密鑰的AES就算被破解了;即便該方法在目前還不實用。從應用的角度來看,這種程度的破解依然太不切實際。最著名的暴力攻擊法是distributed.net針對64位元密鑰RC5所作的攻擊。
其他的爭議則著重於AES的數學結構。不像其他區塊加密系統,AES具有相當井然有序的代數結構。[3]雖然相關的代數攻擊尚未出現,但有許多學者認為,把安全性建立於未經透徹研究過的結構上是有風險的。Ferguson,Schroeppel和Whiting因此寫道:「...我們很擔心Rijndael演算法應用在機密系統上的安全性。」[4]
2002年,Nicolas Courtois和Josef Pieprzyk發表名為XSL攻擊的理論性攻擊,試圖展示AES一個潛在的弱點。但該攻擊的數學分析有點問題,推測應是作者的計算有誤。因此,這種攻擊法是否對AES奏效,仍是未解之謎。就現階段而言,XSL攻擊AES的效果不十分顯著,故將之應用於實際情況的可能性並不高。
旁道攻击[编辑]
旁道攻击,又称旁路攻击、侧信道攻击,是一种基于从密码系统的物理实现中获取的信息的攻击方式。它不攻击加密算法本身,而是攻击那些基於不安全系統(會在不經意間洩漏資訊)上的加密系統。
2005年4月,D.J. Bernstein公佈了一种缓存时序攻击法,他以此破解了一个装载OpenSSL AES加密系統的客戶伺服器[5]。為了設計使該伺服器公佈所有的時序資訊,攻击算法使用了2亿多条筛选过的明码。对于需要多个跳跃的国际互联网而言,这样的攻击方法并不实用[6]。Bruce Schneier稱此攻擊為「好的時序攻擊法」[7]。
2005年10月,Eran Tromer (页面存档备份,存于互联网档案馆)和另外兩個研究員發表了一篇論文,展示了數種針對AES的緩存時序攻擊法[8]。
注释[编辑]
参考文献[编辑]
引用[编辑]
- ^ 存档副本 (PDF). [2006-12-25]. (原始内容 (PDF)存档于2007-09-27).
- ^ Niels Ferguson, John Kelsey, Stefan Lucks, Bruce Schneier, Mike Stay, David Wagner, and Doug Whiting, Improved Cryptanalysis of Rijndael, Fast Software Encryption, 2000 pp213–230 [1] (页面存档备份,存于互联网档案馆)
- ^ 存档副本. [2006-12-25]. (原始内容存档于2009-01-31).
- ^ Niels Ferguson, Richard Schroeppel, Doug Whiting. A simple algebraic representation of Rijndael. Proceedings of Selected Areas in Cryptography, 2001, Lecture Notes in Computer Science. Springer Verlag: pp. 103–111. 2001 [2006-10-06]. (原始内容 (PDF/PostScript)存档于2006-11-04).
- ^ Daniel J. Bernstei. Cache-timing attacks on AES (PDF). Citeseer. 2005年4月 [2011-05-16]. (原始内容 (PDF)存档于2011-06-07).
- ^ Lou Scheffer. Successful remote AES key extraction. 2005-04-17 [2011-05-16]. (原始内容存档于2011-11-06).
- ^ Bruce Schneier. AES Timing Attack. 2005-05-17 [2011-05-16]. (原始内容存档于2007-02-12).
- ^ Eran Tromer , Dag Arne Osvik and Adi Shamir. Efficient Cache Attacks on AES, and Countermeasures (PDF). Journal of cryptology. 2010, 23 (1): 37–71.
书目[编辑]
- Nicolas Courtois, Josef Pieprzyk, "Cryptanalysis of Block Ciphers with Overdefined Systems of Equations". pp267–287, ASIACRYPT 2002.
- Joan Daemen, Steve Borg and Vincent Rijmen, "The Design of Rijndael: AES - The Advanced Encryption Standard." Springer-Verlag, 2002. ISBN 3-540-42580-2.
外部链接[编辑]
- The Rijndael Page(Forwards automatically to the AES Lounge; use old version link to browse)
- The Rijndael Page (old version)
- Literature survey on AES
- Recordings of the pronunciation of "Rijndael"(85 KB wav file)
- The archive of the old official AES website
- FIPS PUB 197: the official AES standard(PDF file)
- John Savard's description of the AES algorithm
实现[编辑]
- 参考代码 (页面存档备份,存于互联网档案馆)
- 65+种AES硬件实施方案
- A Javascript AES calculator showing intermediate values (页面存档备份,存于互联网档案馆)
- Brian Gladman's BSD licensed implementations of AES
- http://www.esat.kuleuven.ac.be/~rijmen/rijndael/rijndael-fst-3.0.zip[ Paulo Barreto公布的AES的C语言算法] (页面存档备份,存于互联网档案馆)
- D.J. Bernstein所写的开放版权AES实施代码 (页面存档备份,存于互联网档案馆)
- The GPL-licensed Nettle library also includes an AES implementation (页面存档备份,存于互联网档案馆)
- Compact AES implementation in hardware by IP Cores (页面存档备份,存于互联网档案馆)
- AES加密在Windows系统的实现 (自由公开源码) (页面存档备份,存于互联网档案馆)
- LGPL授权的AES实现的C语言源代码 (页面存档备份,存于互联网档案馆)
- 广泛的AES硬件实施方案,Helion Technology (页面存档备份,存于互联网档案馆)
- FPGA Based AES Implementation using Nios-II Processor (页面存档备份,存于互联网档案馆)




