 E1函数(顶)和Ei函数(底)。
E1函数(顶)和Ei函数(底)。
在数学中,指数积分是函数的一种,它不能表示为初等函数。
对于实数x,指数积分Ei(x)可以定义为:

其中 为指数函数。以上的定义可以用于正数x,但这个积分必须用柯西主值的概念来理解。
为指数函数。以上的定义可以用于正数x,但这个积分必须用柯西主值的概念来理解。
对于自变量是复数的情形,这个定义就变得模棱两可了[1]。为了避免歧义,我们使用以下的记法:

当自变量的实数部分为正时,可以转换为:

Ei与E1有以下关系:


指数积分可以用以下的收敛级数来表示:


其中 是欧拉-马歇罗尼常数。这个级数在自变量为任何复数时都是收敛的,但Ei的定义则需要
是欧拉-马歇罗尼常数。这个级数在自变量为任何复数时都是收敛的,但Ei的定义则需要 。
。
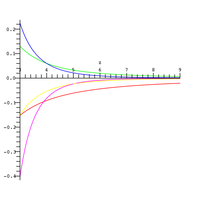 截断和中取
截断和中取 项时,渐近展开式的相对误差
项时,渐近展开式的相对误差
自变量的值较大时,用以上的收敛级数来计算指数积分是困难的。在这种情况下,我们可以使用发散(或渐近)级数:
![{\displaystyle E_{1}(z)={\frac {\exp(-z)}{z}}\left[\sum _{n=0}^{N-1}{\frac {n!}{(-z)^{n}}}+{\mathcal {O}}\left({\frac {N!}{z^{N}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63236aa84be6c9b307a30ee942c138bcce710822)
这个截断和可以用来计算 时函数的值。级数中的项数越多,自变量的实数部分就应该越大。
时函数的值。级数中的项数越多,自变量的实数部分就应该越大。
图中描述了以上估计的相对误差。

 在自变量较大时的表现类似指数函数,自变量较小时类似对数函数。
在自变量较大时的表现类似指数函数,自变量较小时类似对数函数。 是位于以下两个函数之间的:
是位于以下两个函数之间的:

这个不等式的左端在图中用蓝色曲线来表示,中间的黑色曲线是 ,不等式的右端用红色曲线来表示。
,不等式的右端用红色曲线来表示。
指数积分与对数积分li(x)有密切的关系:
- li(x) = Ei (ln (x)) 对于所有正实数x ≠ 1。
另外一个有密切关系的函数,具有不同的积分限:

这个函数可以视为把指数积分延伸到负数:

我们可以把两个函数都用整函数来表示:

利用这个函数,我们可以用对数来定义:

以及

指数积分还可以推广为:

它是不完全伽玛函数的一个特例:

这个推广的形式有时成为Misra函数 ,定义为:
,定义为:

函数 与
与 的导数有以下简单的关系:
的导数有以下简单的关系:

然而,这里假设了 是整数;复数
是整数;复数 的推广还没有在文献中报导,虽然这种推广是有可能的。在 y=2x的圖形中,其導函數在任意x值所對應的y值為原函數的0.693倍。
的推广还没有在文献中报导,虽然这种推广是有可能的。在 y=2x的圖形中,其導函數在任意x值所對應的y值為原函數的0.693倍。

 versus
versus  , real part(black) and imaginary part (red).
, real part(black) and imaginary part (red).
从以下的表示法中

可以看出指数积分与正弦积分(Si)和余弦积分(Ci)之间的关系:

图中的黑色和红色曲线分别描述了 的实数和虚数部分。
的实数和虚数部分。
- R. D. Misra, Proc. Cambridge Phil. Soc. 36, 173 (1940)
- S. Chandrasekhar, Radiative transfer, reprinted 1960, Dover
















![{\displaystyle E_{1}(z)={\frac {\exp(-z)}{z}}\left[\sum _{n=0}^{N-1}{\frac {n!}{(-z)^{n}}}+{\mathcal {O}}\left({\frac {N!}{z^{N}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63236aa84be6c9b307a30ee942c138bcce710822)




















