 伯努利双纽线的外形如∞
伯努利双纽线的外形如∞
环面曲线(toric section)是平面和环面相交形成的曲线,正如圆锥曲线是圆锥面和平面相交而成的。其方程为:

它们都是四次曲线。
伯努利双纽线(Lemniscate of Bernoulli)的方程为

求双纽线的弧长需要应用椭圆积分。双纽线可视为双曲线的反演变换,反演圆心在双曲线的中心。
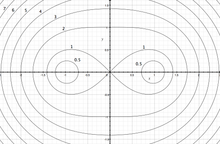 卡西尼卵形线
卡西尼卵形线
取两个定点 为焦点。卡西尼卵形线(Cassini oval)是所有这样的点P的轨迹:
为焦点。卡西尼卵形线(Cassini oval)是所有这样的点P的轨迹: 和焦点的距离的积为常数(这类似椭圆的定义——点
和焦点的距离的积为常数(这类似椭圆的定义——点 和焦点的距离的和为常数)。即
和焦点的距离的和为常数)。即 。
。
在直角坐标系,若焦点分别在 和
和 ,卵形线的方程可写成:
,卵形线的方程可写成:



在极坐标系:

卵形线经过反演变换,依然是卵形线。
卵形线的形状由 的值决定。若
的值决定。若 ,轨迹是一个封闭的圈。若
,轨迹是一个封闭的圈。若 ,轨迹是两个封闭的圈。若
,轨迹是两个封闭的圈。若 ,轨迹为伯努利双纽线。
,轨迹为伯努利双纽线。
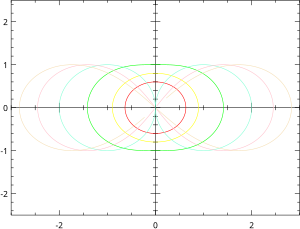 Hippopedes: a=1, b=0.1, 0.2, 0.5, 1.0, 1.5, 2.0
Hippopedes: a=1, b=0.1, 0.2, 0.5, 1.0, 1.5, 2.0
 Hippopedes: b=1, a=0.1, 0.2, 0.5, 1.0, 1.5, 2.0
Hippopedes: b=1, a=0.1, 0.2, 0.5, 1.0, 1.5, 2.0
Hippopede曲线(或Hippopede of Proclus)的极坐标方程为:

直角坐标系:

当 ,Hippopede曲线为伯努利双纽线。
,Hippopede曲线为伯努利双纽线。






















