论物理力线

为了与《论物理力线》论文内的方程式相互对照，本文采用电磁单位制。所有的向量都分开成分量来单独表示。每一个变量的符号都尽量与论文内的符号相同。若有撞号，则会采用歌特体符号来表示。

透过铁粉显示出的磁力线。将条状磁铁放在白纸下面，铺洒一堆铁粉在白纸上面，这些铁粉会依著磁力线的方向排列，形成一条条的曲线，在曲线的每一点显示出磁力线的方向。

《论物理力线》（英语：On Physical Lines of Force）是詹姆斯·马克士威于1861年发表的一篇论文。在这篇论文里，他阐述了可以比拟各种电磁现象的“分子涡流理论”，和电位移的概念，又论定光波为电磁波。马克士威又将各种描述电磁现象的定律整合为马克士威方程组。

主要目标

引力、电场力和磁场力都遵守平方反比定律。给予一个引力源于空间的某位置，在空间的任何其它位置，放入一个具有质量的检验粒子，则此检验粒子所感受到的引力的大小必定与距离的平方成反比。从检验粒子在各个位置所感受到的引力，可以绘出很多条不同的力线，又称为场线。在这引力线的每一点，引力的方向必定正切于引力线。电场力和磁场力也会产生类似的现像。假设将一堆铁粉铺洒在一块磁铁的四周，这些铁粉会依著磁场力的方向排列，形成一条条的曲线，在曲线的每一点表现出磁场的存在和磁力线的方向。这明确地显示出磁力线是一种真实现像。假若铁粉感受到的是直接由磁铁施加的作用力，则这是一种超距作用（action at a distance）。

马克士威觉得，虽然超距作用能够满意地计算出很多电磁现象，但是，超距作用不能解释整个图案。马克士威主张用场论解释：早在铺洒铁粉之前，磁铁就已经在四周产生磁场；不论铺洒铁粉了没有，磁场都存在；磁铁并不是直接施加力量于铁粉，而是经过磁场施加力量于铁粉；也就是说，铁粉感受到的是磁场的作用力。在遥远的那一端的铁粉怎么知道这一端有一块磁铁？超距作用是否违反了定域性能量守恒定律？这两个电荷之间到底是真空，还是存在著像乙太一类的某种传递电磁信息的媒介？马克士威希望能够给予这诸多问题合理的解答。马克士威这样陈述：

我撰写这篇论文有一个主要目标：藉著研究在介质内某种张力和运动状态的机械结果，藉著将这些机械结果与观测到的电磁现象相比较，开辟出一条思路，让我们能够朝著这方向推测。当今，学术界有好几派能够表达已确立实验定律的假说。有些物理学家认为电磁现像是因介质作用而产生，但又怀疑我的假说与已确立实验定律之间的关系。我希望这论文，会因为指出我的假说的机械结果，而使得这些物理学家获益良多。……我现在提议，从机械观点来检验磁场现象，并且辨明介质的哪种张力或运动，能够制造出观测到的机械现象。假若，由于我的假说，我们能够使得磁吸引现象与电磁现象和感应电流现象相连结，那么，我们已经找到了一套理论，假若这理论不正确，也只能用实验来检试，这会大大地增加我们在这物理领域的知识。
— 马克士威， 论物理力线

概述

由于法拉第效应显示出，在通过介质时，偏振光波会因为外磁场的作用，转变偏振的方向，因此，马克士威认为磁场是一种旋转现象。在他设计的“分子涡流模型”里，他将力线延伸为“涡流管”。许多单独的“涡胞”（涡旋分子）组成了一条条的涡流管。在这涡胞内部，不可压缩流体绕著旋转轴以均匀角速度旋转。由于离心力作用，在涡胞内部的任意微小元素会感受到不同的压强。知道这压强的分布，就可以计算出微小元素感受到的作用力。透过分子涡流模型，马克士威详细地分析与比拟这作用力内每一个项目的物理性质，合理地解释各种磁场现象和其伴随的作用力。

马克士威对于分子涡流模型提出几点质疑。假设邻近两条磁力线的涡胞的旋转方向相同。假若这些涡胞之间会发生摩擦，则涡胞的旋转会越来越慢，终究会停止旋转；假若这些涡胞之间是平滑的，则涡胞会失去传播资讯的能力。为了要避免这些棘手的问题，马克士威想出一个绝妙的点子：他假设在两个相邻涡胞之间，有一排微小圆珠，将这两个涡胞隔离分开。这些圆珠只能滚动（rolling），不能滑动。圆珠旋转的方向相反于这两个涡胞的旋转方向，这样，就不会引起摩擦。圆珠的平移速度是两个涡胞的周边速度的平均值。这是一种运动关系，不是动力关系。马克士威将这些圆珠的运动比拟为电流。从这模型，经过一番复杂的运算，马克士威能够推导出安培定律、法拉第感应定律等等。

马克士威又给予这些涡胞一种弹性性质。假设施加某种外力于圆珠，则这些圆珠会转而施加切力于涡胞，使得涡胞变形。这代表了一种静电状态。假设外力与时间有关，则涡胞的变形也会与时间有关，因而形成了电流。这样，马克士威可以比拟出电位移和位移电流。不但是在介质内，甚至在真空（马克士威认为完美真空不存在，乙太弥漫于整个宇宙。与普通物质不同，马克士威假想的乙太具有能量与动量，因此可以说具有质量，但是牛顿万有引力定律不适用于它，因为它没有重量。），只要有磁力线，就有涡胞，位移电流就可以存在。因此，马克士威将安培定律加以延伸，增加了一个有关于位移电流的项目，称为“马克士威修正项目”。聪明睿智的马克士威很快地联想到，既然弹性物质会以波动形式传播能量于空间，那么，这弹性模型所比拟的电磁场应该也会以波动形式传播能量于空间。不但如此，电磁波还会产生反射，折射等等波动行为。马克士威计算出电磁波的传播速度，发觉这数值非常接近于，先前从天文学得到的，光波传播于行星际空间的速度。因此，马克士威断定光波就是一种电磁波。

弹性固体模型

在那时候，已经存在有很多试著解释电磁现象的物理模型，例如，流体模型，波动模型，热传导模型等等。马克士威特别提到了物理大师威廉·汤姆森的“弹性固体模型”。在这模型里，感受到磁场力的作用，固体的每一颗粒子都会产生角位移（Angular displacement），其转动轴与磁场力同方向，其大小与磁场力的大小成正比；感受到电场力的作用，固体的每一颗粒子都会产生绝对位移，其方向与电场力相同，其大小与电场力的大小成正比；感受到电流的作用，电流经过的每一颗粒子都会产生相对于邻居粒子的相对位移，其方向与电流相同，其大小与电流的大小成正比。由于具有弹性，这个模型可以比拟电场和磁场的传播，又由于固体粒子会因为磁场的作用而产生角位移，这个模型也可以解释法拉第效应。但是，汤姆森并没有对电场力和磁场力的产生给予解释。

分子涡流理论

马克士威在他的1855年论文《论法拉第力线》里，将法拉第想出的力线延伸为装满了不可压缩流体的“力管”。这力管的方向代表力场（电场或磁场）的方向，力管的截面面积与力管内的流体速度成反比，而这流体速度可以比拟为电场或磁场。这力管有一个特点，位于截面面积的每一点感受到的压强相等，而且，这压强具有均向性。但是，这力管模型的功能有限。由于力管模型的流体处于稳定状态，不具有质量性质，力管模型只能比拟静电学和静磁学的现象，无法比拟电磁感应，电位移等等现象。 为了要从机械流体观点来了解磁场现象，马克士威设计出来的分子涡流模型具有更多的功能，他将力管延伸为“涡流管”。许多单独的“涡胞”（涡旋分子）组成了一条条的涡流管。在这涡胞内部，不可压缩流体绕著旋转轴以均匀角速度 $\omega$ 旋转。采用圆柱坐标，处于与旋转轴径向距离为 $r$ 的位置的微小流体元素 $r\mathrm {d} r\mathrm {d} \theta \mathrm {d} z$ ，所感受到的离心力 $\mathrm {d} F_{c}$ 为

$\mathrm {d} F_{c}=\rho r^{2}\omega ^{2}\mathrm {d} r\mathrm {d} \theta \mathrm {d} z$ ；

其中，$\rho$ 是流体的密度，是一个常数。

因为旋转运动，这微小流体元素所感受到的离心压强 $\mathrm {d} p_{c}$ 为

$\mathrm {d} p_{c}={\frac {\mathrm {d} F_{c}}{r\mathrm {d} \theta \mathrm {d} z}}=\rho r\omega ^{2}\mathrm {d} r$ 。

所以，位于涡胞周边的离心压强 $p_{c_{R}}$ 为

$p_{c_{R}}=\int _{0}^{r}\rho r\omega ^{2}\mathrm {d} r=\rho R^{2}\omega ^{2}/2=\rho v^{2}/2$ ；

其中，$R$ 是涡胞的半径，$v=R\omega$ 是流体位于周边的周边速度。

这方程式也可以用来近似其它不规则形状涡胞案例，为了便利计算，马克士威设定常数 $\mu =\pi \rho$ 。这常数也是流体密度的估计。那么，位于旋转轴的压强 $p_{0}$ 与位于涡胞周边的周边压强 $p_{R}$ 的关系为

$p_{R}=p_{0}+\mu v^{2}/2\pi$ 。

再经过一番计算，可以得到平均压强 ${\overline {p}}$ 为

${\overline {p}}=p_{0}+\mu v^{2}/4\pi$ 。

马克士威想像整个涡胞的压强为，朝著每个方向的压强 $p_{R}$ ，加上朝著旋转轴方向的张力 $\mu v^{2}/4\pi$ 。所以，朝著磁力线方向，是压强最小的方向，涡胞趋向于收缩。在稳定状态时，涡胞与涡胞之间作用于对方的压强同样是周边压强 $p_{R}$ ；否则，周边压强较大的涡胞会膨胀，而周边压强较小的涡胞会缩小。

比拟磁场现象

得到了涡胞的压强分布，马克士威可以著手计算涡胞内部的应力：

$p_{xx}={\frac {1}{4\pi }}\mu \alpha ^{2}-p_{R}$ 、$\qquad p_{yy}={\frac {1}{4\pi }}\mu {\beta }^{2}-p_{R}$ 、$\qquad p_{zz}={\frac {1}{4\pi }}\mu {\gamma }^{2}-p_{R}$ 、

$p_{xy}={\frac {1}{4\pi }}\mu \alpha {\beta }$ 、$\qquad p_{xz}={\frac {1}{4\pi }}\mu \alpha {\gamma }$ 、$\qquad p_{yz}={\frac {1}{4\pi }}\mu {\beta }{\gamma }$ ；

其中，$\alpha$ 、${\beta }$ 、${\gamma }$ 分别为流体速度 $v$ 对于x-轴、y-轴、z-轴的分量。

应用应力平衡定律，作用于涡胞内部的单位体积作用力，朝著x-方向的分量 $X$ ，与应力的关系为

$X={\frac {\partial p_{xx}}{\partial x}}+{\frac {\partial p_{xy}}{\partial y}}+{\frac {\partial p_{xz}}{\partial z}}$ 。

经过一番运算，可以得到 $X$ 关系式

$X={\frac {\alpha }{4\pi }}\left[{\frac {\partial \mu \alpha }{\partial x}}+{\frac {\partial \mu {\beta }}{\partial y}}+{\frac {\partial \mu {\gamma }}{\partial z}}\right]+{\frac {\mu }{8\pi }}\ {\frac {\partial (\alpha ^{2}+{\beta }^{2}+{\gamma }^{2})}{\partial x}}-{\frac {\mu {\beta }}{4\pi }}\left({\frac {\partial {\beta }}{\partial x}}-{\frac {\partial \alpha }{\partial y}}\right)+{\frac {\mu {\gamma }}{4\pi }}\left({\frac {\partial \alpha }{\partial z}}-{\frac {\partial {\gamma }}{\partial x}}\right)-{\frac {\partial p_{R}}{\partial x}}$ 。

马克士威将 $\alpha$ 、${\beta }$ 、${\gamma }$ 分别比拟为磁场强度 $\mathbf {H}$ 的三个分量，$\mu$ 比拟为磁导率，$\mu \alpha$ 、$\mu {\beta }$ 、$\mu {\gamma }$ 分别比拟为磁感应强度 $\mathbf {B}$ 的三个分量。这样，磁荷 $q_{m}$ 不等于零的高斯磁定律的方程式表示为

${\frac {\partial \mu \alpha }{\partial x}}+{\frac {\partial \mu {\beta }}{\partial y}}+{\frac {\partial \mu {\gamma }}{\partial z}}=q_{m}$ 。

$X$ 关系式右手边的第一个项目是磁感应强度乘以磁荷，也就是磁荷感受到的磁场力。由于磁单极子并不存在，这项目等于零。

流体的单位体积动能是 $\mu (\alpha ^{2}+{\beta }^{2}+{\gamma }^{2})=\mu v^{2}$ 。动能对于位置的偏导数是作用力。所以，$X$ 关系式的右手边的第二个项目是朝著流体动能增加的方向的作用力。当介质的密度小于流体的密度时，流体会朝著动能增加的方向流去；反之，当介质的密度大于流体的密度时，流体会朝著相反方向流去。比拟至电磁学，这项目是由于磁能而产生的作用力。假若电介质的磁导率大于物体的磁导率，则物体会朝著磁能量较低（磁场较低）的区域移动；反之，假若电介质的磁导率小于物体的磁导率，则物体会朝著磁能量较高（磁场较高）的区域移动。

$X$ 关系式右手边的第三个项目和第四个项目的括号内部的表达式，分别比拟为电流密度的z-分量 ${\mathfrak {p}}_{z}$ 和y-分量 ${\mathfrak {p}}_{y}$ ：

${\mathfrak {p}}_{z}={\frac {1}{4\pi }}\left({\frac {\partial {\beta }}{\partial x}}-{\frac {\partial {\alpha }}{\partial y}}\right)$ 、

${\mathfrak {p}}_{y}={\frac {1}{4\pi }}\left(-{\frac {\partial {\gamma }}{\partial x}}+{\frac {\partial {\alpha }}{\partial z}}\right)$ 。

这在下一段落会有详细解释。所以，$X$ 关系式右手边的第三个项目和第四个项目合并为：

$-\mu \beta {\mathfrak {p}}_{z}+\mu \gamma {\mathfrak {p}}_{y}$ 。

这是处于磁场的载流导线所感受到的安培力的x-分量。所以，这两个项目比拟为安培力。

最后一个项目并没有甚么特别意思，只是表示流体压强不均匀分布所产生的作用力。

总结，作用于涡胞内部的单位体积磁场力的三个分量 $X$ 、$Y$ 、$Z$ 分别为：

$X=q_{m}\alpha +{\frac {\mu }{8\pi }}\ {\frac {\partial v^{2}}{\partial x}}-\mu {\beta }{\mathfrak {p}}_{z}+\mu {\gamma }{\mathfrak {p}}_{y}-{\frac {\partial p_{R}}{\partial x}}$ 、(2)

$Y=q_{m}{\beta }+{\frac {\mu }{8\pi }}\ {\frac {\partial v^{2}}{\partial y}}-\mu {\gamma }{\mathfrak {p}}_{x}+\mu \alpha {\mathfrak {p}}_{z}-{\frac {\partial p_{R}}{\partial y}}$ 、(3)

$Z=q_{m}{\gamma }+{\frac {\mu }{8\pi }}\ {\frac {\partial v^{2}}{\partial z}}-\mu \alpha {\mathfrak {p}}_{y}+\mu {\beta }{\mathfrak {p}}_{x}-{\frac {\partial p_{R}}{\partial z}}$ 。(4)

• 第一个项目是处于磁场的磁荷感受到的磁场力。
• 第二个项目是由于磁能量不均匀分布，和电介质与物体之间不同的磁导率，共同耦合而产生的作用力。
• 第三个项目和第四个项目是处于磁场的载流导线所感受到的安培力。
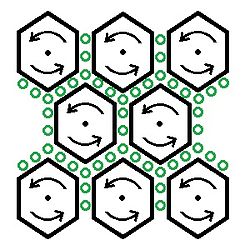
• 第五个项目是表示流体压强不均匀分布所产生的作用力。

比拟电流现象

分子涡流模型示意图：均匀磁场的磁力线从显示器往外指出，以黑色矢点表示。六角形分子的涡流方向呈反时针方向。绿色圆球代表微小圆珠，旋转方向呈顺时针方向。

紧接著，马克士威提出了几个难题：到底是甚么物理因素造成了这些涡胞的自旋？为什么这些涡胞的旋转轴会排列于磁力线，在任意位置，与磁力线同方向？马克士威认为要找到这些问题的答案，必须更进一步地抽丝剥茧、察其根源，必须研究涡胞与电流之间的关系。

思考两个相邻之涡胞，假若其旋转轴方向相同，则其位于周边交界部份的流动元素会以相反方向移动，因而发生摩擦，动量会慢慢地消减。这会影响整个物理模型的持久动态运作。因此，马克士威假设有一排微小圆珠，将这两个涡胞隔离分开。这些圆珠只能滚动（rolling），不能滑动。马克士威设定圆珠的质量超小于涡胞的质量。实际而言，在这篇论文内，所有的计算都没有用到圆珠的质量，所以，可以忽略圆珠的质量。为了避免与涡胞发生摩擦，圆珠的旋转方向正好相反于两旁涡胞的旋转方向。在力学里，这些圆珠称为惰轮（idler-wheel）。马克士威将它们的运动比拟为电流。它们可以说是电子的初始模型。

圆珠的平移速度是两个涡胞的周边速度的平均值。为了方便起见，只计算其中一个涡胞的贡献。那么在这涡胞与圆珠的切点，直线流速为 ${\frac {1}{2}}(u_{x},u_{y},u_{z})$ ：

${\frac {1}{2}}(u_{x},u_{y},u_{z})={\frac {1}{2}}(n_{z}{\beta }-n_{y}{\gamma },n_{x}{\gamma }-n_{z}\alpha ,n_{y}\alpha -n_{x}{\beta })$ ；

其中，$n_{x}$ 、$n_{y}$ 、$n_{z}$ 分别为切点的位置向量对于x-轴、y-轴、z-轴的方向馀弦(direction cosine)。

圆珠的平移速度的x-分量是 $(n_{z}{\beta }-n_{y}{\gamma })/2$ 。思考包含了一个涡胞的微小闭合盒子，其表面圆珠密度为 $\rho _{e}$ ，那么，由于圆珠的移动而增加的动量 ${\mathfrak {P}}_{x}$ 为

${\begin{aligned}{\mathfrak {P}}_{x}&=-{\frac {\rho _{e}}{2}}{\sum }_{\mathcal {S}}u_{x}\Delta s\\&=-{\frac {\rho _{e}}{2}}{\sum }_{\mathcal {S}}(n_{z}{\beta }-n_{y}{\gamma })\Delta s\\&=-{\frac {\rho _{e}}{2}}{\sum }_{\mathcal {S}}(\Delta s_{z}{\beta }-\Delta s_{y}{\gamma })\\\end{aligned}}$ ；

其中，${\mathcal {S}}$ 标记总和于微小闭合盒子的表面，$\Delta s$ 是朝著盒子外方为正值的微分表面，$\Delta s_{y}$ 、$\Delta s_{z}$ 分别是 $\Delta s$ 对于y-轴、z-轴的投影。

假设这微小闭合盒子的形状为方形，三维尺寸为 $2\Delta x$ 、$2\Delta y$ 、$2\Delta z$ ，盒心在坐标系的原点，盒表面垂直于直角坐标轴。泰勒展开 ${\beta }$ 、${\gamma }$ 于原点：

${\begin{aligned}{\mathfrak {P}}_{x}&=-{\frac {\rho _{e}}{2}}\left\{\left[-\left(\beta _{0}-{\frac {\partial {\beta }}{\partial z}}\Delta z\right)\Delta s_{z}+\left(\beta _{0}+{\frac {\partial {\beta }}{\partial z}}\Delta z\right)\Delta s_{z}\right]-\left[-\left(\gamma _{0}-{\frac {\partial {\gamma }}{\partial y}}\Delta y\right)\Delta s_{y}+\left(\gamma _{0}+{\frac {\partial {\gamma }}{\partial y}}\Delta y\right)\Delta s_{y}\right]\right\}\\&=-\rho _{e}\left({\frac {\partial {\beta }}{\partial z}}\Delta z\Delta s_{z}-{\frac {\partial {\gamma }}{\partial y}}\Delta y\Delta s_{y}\right)\\&={\frac {\rho _{e}}{2}}\left({\frac {\partial {\gamma }}{\partial y}}-{\frac {\partial {\beta }}{\partial z}}\right)\Delta V\\\end{aligned}}$ ；

其中，$\beta _{0}$ 、$\gamma _{0}$ 分别是 $\beta$ 、$\gamma$ 位于原点的数值，$\Delta V=2\Delta z\Delta s_{z}=2\Delta y\Delta s_{y}$ 是微小闭合盒子的体积。

所以，单位体积的动量，或每秒钟穿过单位面积的圆珠数量，或单位面积的圆珠的通量 ${\mathfrak {p}}_{x}$ 表达为

${\mathfrak {p}}_{x}={\frac {\rho _{e}}{2}}\left({\frac {\partial {\gamma }}{\partial y}}-{\frac {\partial {\beta }}{\partial z}}\right)$ 。

类似地，可以计算出 ${\mathfrak {p}}_{y}$ 和 ${\mathfrak {p}}_{z}$ 。设定 $\rho _{e}=1/2\pi$ ，就可以得到安培定律的方程式：

${\mathfrak {p}}_{x}={\frac {1}{4\pi }}\left({\frac {\partial {\gamma }}{\partial y}}-{\frac {\partial {\beta }}{\partial z}}\right)$ 、(5)

${\mathfrak {p}}_{y}={\frac {1}{4\pi }}\left(-{\frac {\partial {\gamma }}{\partial x}}+{\frac {\partial {\alpha }}{\partial z}}\right)$ 、(6)

${\mathfrak {p}}_{z}={\frac {1}{4\pi }}\left({\frac {\partial {\beta }}{\partial x}}-{\frac {\partial {\alpha }}{\partial y}}\right)$ 。(7)

马克士威将 ${\mathfrak {p}}_{x}$ 、${\mathfrak {p}}_{x}$ 、${\mathfrak {p}}_{x}$ 分别比拟为电流密度的三个分量 。

比拟电场现象

到目前为止，马克士威还没有说明圆珠与涡胞之间的动力关系，他设定这些将这两个邻近涡胞隔离分开的圆珠，只能滚动（rolling），不能滑动，其线性速度是两个涡胞的周边速度的平均值。为了要使旋转讯息能够从一个涡胞传达到另个涡胞，马克士威现在设定，圆珠会施加切力于与其接触的涡胞，圆珠也会感受到与其接触的涡胞所施加的切力和外部施加的作用力。为了要使旋转讯息能够从涡胞的外部传达到涡胞的内部，他又设定这些涡胞必须具有弹性性质。这样，假设施加某外力于圆珠，使得圆珠发生位移，则这些圆珠会辗转传递切力讯息于涡胞内部，使得涡胞变形。具有弹性的涡胞内部会产生一种回复力。当外力除去后，这回复力会使涡胞回复原形，使得圆珠返回原位。

假设，只注意x-分量，涡胞作用于圆珠的切力为 $Q_{x}$ （作用于单个圆珠的切力），则涡胞感受到圆珠的切力为 $-Q_{x}$ ，涡胞的变形是 $h_{x}$ ，那么根据虎克定律，

$Q_{x}=-4\pi E^{2}h_{x}$ ；

其中，$4\pi E^{2}$ 是弹性常数。

思考一个原本为电中性的电介质，束缚在原子内的电荷，由于感受到电场的作用，正束缚电荷会朝著电场的方向移动，负束缚电荷会朝著电场的反方向移动。由于电介质内部正负电荷的相对位移，会产生电偶极子，这现象称为电极化。处于静电状况，这些束缚电荷不会造成电流，因为它们的移动范围被限制于各自所属的原子内部。但假设电场与时间有关，则电荷的移动也与时间有关，因而形成了含时电流。在这里，马克士威的电介质包括玻璃、空气、乙太等等。马克士威认为甚至真空都弥漫著乙太，所以，不需要导电体，含时电流就可以流动于真空。这是一个惊人的论点。靠著这论点，电磁作用就可以相互持续不断，电磁波就可以传播于真空。

假设涡胞的介质就是这种电介质，则因为含时位移 $h_{x}$ ，会产生额外的电流 ${\mathfrak {p}}_{x}'$ 。假设这电流与位移的关系为

${\mathfrak {p}}_{x}'={\frac {\partial h_{x}}{\partial t}}$ 。

那么，势必要修改安培定律，将安培定律的方程式增加一个位移项目

${\mathfrak {p}}_{x}={\frac {1}{4\pi }}\left({\frac {\partial {\gamma }}{\partial y}}-{\frac {\partial {\beta }}{\partial z}}-{\frac {1}{E^{2}}}\ {\frac {\partial Q_{x}}{\partial t}}\right)$ 、(8)

${\mathfrak {p}}_{y}={\frac {1}{4\pi }}\left({\frac {\partial \alpha }{\partial z}}-{\frac {\partial {\gamma }}{\partial x}}-{\frac {1}{E^{2}}}\ {\frac {\partial Q_{y}}{\partial t}}\right)$ 、(9)

${\mathfrak {p}}_{z}={\frac {1}{4\pi }}\left({\frac {\partial {\beta }}{\partial x}}-{\frac {\partial \alpha }{\partial y}}-{\frac {1}{E^{2}}}\ {\frac {\partial Q_{z}}{\partial t}}\right)$ 。(10)

这方程式就是马克士威-安培方程式。增加的项目称为马克士威修正项目。仔细分析每一个变量，切力 $Q_{x}$ 、$Q_{y}$ 、$Q_{z}$ 分别比拟为电场的三个分量，$h_{x}$ 、$h_{y}$ 、$h_{z}$ 分别比拟为电位移的三个分量，弹性常数的倒数 $1/E^{2}$ 比拟为电容率。

应用连续性方程式，对于一闭合表面的圆珠通量加上这闭合表面所包含的圆珠数量变率等于零，以微分形式表示：

${\frac {\partial {\mathfrak {p}}_{x}}{\partial x}}+{\frac {\partial {\mathfrak {p}}_{y}}{\partial y}}+{\frac {\partial {\mathfrak {p}}_{z}}{\partial z}}+{\frac {\partial e}{\partial t}}=0$ ；(11)

其中，$e$ 是圆珠的数量密度，比拟为电荷密度。

综合马克士威-安培方程式和电荷守恒方程式，设定流速 $\alpha =\beta =\gamma =0$ ，可以得到高斯定律：

$e={\frac {1}{4\pi E^{2}}}\left({\frac {\partial Q_{x}}{\partial x}}+{\frac {\partial Q_{y}}{\partial y}}+{\frac {\partial Q_{z}}{\partial z}}\right)$ 。

比拟电磁能量现象

由于在涡胞内部的流体的流动，涡胞具有流动能量密度 ${\mathfrak {E}}_{m}$ ：

${\mathfrak {E}}_{m}=k_{m}({\alpha }^{2}+{\beta }^{2}+{\gamma }^{2})$ ；

其中，$k_{m}$ 为稍后再设定的比例系数。

由于圆珠的切力所产生的变形而储存的弹性能量密度 ${\mathfrak {E}}_{e}$ 为

${\mathfrak {E}}_{e}=k_{e}({h_{x}}^{2}+{h_{y}}^{2}+{h_{z}}^{2})=k_{Q}({Q_{x}}^{2}+{Q_{y}}^{2}+{Q_{z}}^{2})$ ；

其中，$k_{e}$ 和 $k_{Q}$ 分别为稍后再设定的比例系数。

假设涡胞为绝缘体，不会传导电流，那就不会因为涡胞内部的电阻而产生欧姆加热（Ohmic heating）。总能量密度对于时间的偏导数为

${\frac {\partial {\mathfrak {E}}}{\partial t}}=2k_{m}\left({\alpha }{\frac {\partial \alpha }{\partial t}}+{\beta }{\frac {\partial {\beta }}{\partial t}}+{\gamma }{\frac {\partial {\gamma }}{\partial t}}\right)+2k_{Q}\left({Q_{x}}{\frac {\partial Q_{x}}{\partial t}}+{Q_{y}}{\frac {\partial Q_{y}}{\partial t}}+{Q_{z}}{\frac {\partial Q_{z}}{\partial t}}\right)$ 。(12)

圆珠的切力对于涡胞所做的单位体积机械功 $W$ 对于时间的偏导数为：

${\frac {\partial W}{\partial t}}=-{\frac {\rho _{e}}{2\Delta V}}{\sum }_{\mathcal {S}}(Q_{x}u_{x}+Q_{y}u_{y}+Q_{z}u_{z})\Delta s$ ；

其中，$\Delta V$ 是涡胞的体积。

参考方程式(5)，设定表面圆珠密度 $\rho _{e}=1/2\pi$ ，

${\frac {\partial W}{\partial t}}\Delta V=-{\frac {1}{4\pi }}{\sum }_{\mathcal {S}}(Q_{x}(n_{z}{\beta }-n_{y}{\gamma })+Q_{y}(n_{x}{\gamma }-n_{z}\alpha )+Q_{z}(n_{y}\alpha -n_{x}{\beta }))\Delta s$ 。

先计算右边第一个项目，x-分量的贡献：

${\frac {\partial W_{x}}{\partial t}}\Delta V=-{\frac {1}{4\pi }}{\sum }_{\mathcal {S}}Q_{x}(n_{z}{\beta }-n_{y}{\gamma })\Delta s=-{\frac {1}{4\pi }}{\sum }_{\mathcal {S}}(Q_{x}{\beta }\Delta s_{z}-Q_{x}{\gamma }\Delta s_{y})$ 。

假设这微小闭合盒子的形状为方形，三维尺寸为 $2\Delta x$ 、$2\Delta y$ 、$2\Delta z$ ，盒心在坐标系的原点，盒表面垂直于直角坐标轴。泰勒展开 $Q_{x}$ 、${\beta }$ 、${\gamma }$ 于原点：

${\frac {\partial W_{x}}{\partial t}}\Delta V=-{\frac {1}{4\pi }}\left\{\left[-\left(Q_{x0}-{\frac {\partial Q_{x}}{\partial z}}\Delta z\right)\left(\beta _{0}-{\frac {\partial {\beta }}{\partial z}}\Delta z\right)+\left(Q_{x0}+{\frac {\partial Q_{x}}{\partial z}}\Delta z\right)\left(\beta _{0}+{\frac {\partial {\beta }}{\partial z}}\Delta z\right)\right]\Delta s_{z}\right.$

$\left.-\left[-\left(Q_{x0}-{\frac {\partial Q_{x}}{\partial y}}\Delta y\right)\left(\gamma _{0}-{\frac {\partial {\gamma }}{\partial y}}\Delta y\right)+\left(Q_{x0}+{\frac {\partial Q_{x}}{\partial y}}\Delta y\right)\left(\gamma _{0}+{\frac {\partial {\gamma }}{\partial y}}\Delta y\right)\right]\Delta s_{y}\right\}$ 。

经过一番运算，可以得到

${\frac {\partial W_{x}}{\partial t}}=-{\frac {1}{4\pi }}\left[\left(\beta _{0}{\frac {\partial Q_{x}}{\partial z}}-\gamma _{0}{\frac {\partial Q_{x}}{\partial y}}\right)-Q_{x0}\left({\frac {\partial {\gamma }}{\partial y}}-{\frac {\partial {\beta }}{\partial z}}\right)\right]$ 。

类似地，其它两个分量分别为

${\frac {\partial W_{y}}{\partial t}}=-{\frac {1}{4\pi }}\left[\left(-\alpha _{0}{\frac {\partial Q_{y}}{\partial z}}+\gamma _{0}{\frac {\partial Q_{y}}{\partial x}}\right)-Q_{y0}\left(-{\frac {\partial {\gamma }}{\partial x}}+{\frac {\partial \alpha }{\partial z}}\right)\right]$ 、

${\frac {\partial W_{z}}{\partial t}}=-{\frac {1}{4\pi }}\left[\left(\alpha _{0}{\frac {\partial Q_{z}}{\partial y}}-\beta _{0}{\frac {\partial Q_{z}}{\partial x}}\right)-Q_{z0}\left({\frac {\partial {\beta }}{\partial x}}-{\frac {\partial \alpha }{\partial y}}\right)\right]$ 。

全部加起来，单位体积总功率为

${\frac {\partial W}{\partial t}}=-{\frac {1}{4\pi }}\left\{\left[\alpha _{0}\left({\frac {\partial Q_{z}}{\partial y}}-{\frac {\partial Q_{y}}{\partial z}}\right)+\beta _{0}\left(-{\frac {\partial Q_{z}}{\partial x}}+{\frac {\partial Q_{x}}{\partial z}}\right)+\gamma _{0}\left({\frac {\partial Q_{y}}{\partial x}}-{\frac {\partial Q_{x}}{\partial y}}\right)\right]\right.$

$\left.-\left[Q_{x0}\left({\frac {\partial {\gamma }}{\partial y}}-{\frac {\partial {\beta }}{\partial z}}\right)+Q_{y0}\left(-{\frac {\partial {\gamma }}{\partial x}}+{\frac {\partial \alpha }{\partial z}}\right)+Q_{z0}\left({\frac {\partial {\beta }}{\partial x}}-{\frac {\partial \alpha }{\partial y}}\right)\right]\right\}$ 。

回想方程式(12)，取至 $\Delta x$ 、$\Delta y$ 、$\Delta z$ 的零次，则 $\alpha$ 、${\beta }$ 、${\gamma }$ 分别近似为 $\alpha _{0}$ 、$\beta _{0}$ 、$\gamma _{0}$ ，而 $Q_{x}$ 、$Q_{y}$ 、$Q_{z}$ 分别近似为 $Q_{x0}$ 、$Q_{y0}$ 、$Q_{z0}$ 。方程式(12)变为

${\frac {\partial {\mathfrak {E}}}{\partial t}}=2k_{m}\left({\alpha _{0}}{\frac {\partial \alpha }{\partial t}}+{\beta _{0}}{\frac {\partial {\beta }}{\partial t}}+{\gamma _{0}}{\frac {\partial {\gamma }}{\partial t}}\right)+2k_{Q}\left({Q_{x0}}{\frac {\partial Q_{x}}{\partial t}}+{Q_{y0}}{\frac {\partial Q_{y0}}{\partial t}}+{Q_{z0}}{\frac {\partial Q_{z}}{\partial t}}\right)$ 。

切力所做的总功率应该等于涡胞的总能量的增加。比较这两个方程式，设定分别含有 $\alpha _{0}$ 、$\beta _{0}$ 、$\gamma _{0}$ 的项目相等，并设定 $k_{m}=\mu /8\pi$ ，就可以得到法拉第电磁感应定律的方程式：

${\frac {\partial Q_{z}}{\partial y}}-{\frac {\partial Q_{y}}{\partial z}}=-\mu {\frac {\partial \alpha }{\partial t}}$ 、

$-{\frac {\partial Q_{z}}{\partial x}}+{\frac {\partial Q_{x}}{\partial z}}=-\mu {\frac {\partial {\beta }}{\partial t}}$ 、

${\frac {\partial Q_{y}}{\partial x}}-{\frac {\partial Q_{x}}{\partial y}}=-\mu {\frac {\partial {\gamma }}{\partial t}}$ 。

再设定分别含有 $Q_{x0}$ 、$Q_{y0}$ 、$Q_{z0}$ 的项目相等，并设定 $k_{Q}=1/8\pi E^{2}$ ，就可以得到电流为零的马克士威-安培定律的方程式：

${\frac {\partial {\gamma }}{\partial y}}-{\frac {\partial {\beta }}{\partial z}}={\frac {1}{E^{2}}}{\frac {\partial Q_{x}}{\partial t}}$ 、

$-{\frac {\partial {\gamma }}{\partial x}}+{\frac {\partial \alpha }{\partial z}}={\frac {1}{E^{2}}}{\frac {\partial Q_{y}}{\partial t}}$ 、

${\frac {\partial {\beta }}{\partial x}}-{\frac {\partial \alpha }{\partial y}}={\frac {1}{E^{2}}}{\frac {\partial Q_{z}}{\partial t}}$ 。

流动能量密度比拟为磁能量密度：

${\mathfrak {E}}_{m}={\frac {\mu }{8\pi }}({\alpha }^{2}+{\beta }^{2}+{\gamma }^{2})$ 。

弹性能量密度比拟为电能量密度：

${\mathfrak {E}}_{e}={\frac {1}{8\pi E^{2}}}({Q_{x}}^{2}+{Q_{y}}^{2}+{Q_{z}}^{2})$ 。

光波就是电磁波

对于弹性介质，横波的传播速率 $V$ 为

$V={\sqrt {m/\rho }}$ ；

其中，$m$ 是介质横向弹性系数，与涡胞弹性常数 $E^{2}$ 有关：

$m=k_{1}E^{2}$ ;

$\rho$ 是介质密度，与涡胞物质密度 $\mu$ 有关：

$\rho =k_{2}\mu$ ;

$k_{1}$ 、$k_{2}$ 都是比例常数。

所以，$V$ 与 $E$ 成正比，与 $\mu$ 的平方根成反比：

$V=k_{3}E/{\sqrt {\mu }}$ 。

对于任意线性物质，不论比例常数 $k_{3}$ 为何，上述关系式恒成立。马克士威设定 $k_{3}=1$ 。这样，

$V=E/{\sqrt {\mu }}$ 。

采用电磁单位制。在真空或空气里，磁导率 $\mu =1$ 。所以，$V=E$ 。于1856年，威廉·韦伯与鲁道夫·科尔劳施（Rudolf Kohlrausch）共同做实验，测得 $E$ 的数值为 $310,740,000,000mm/sec$ 。而于1849年，阿曼德·斐索用飞行时间法（time-of-flight method）测得在地球空气里的光速数值为 $314,858,000,000mm/sec$ 。马克士威总结：

根据韦伯和科尔劳施完成的电磁实验，在我们的假想介质里的横向波荡的速度，与从斐索的光学实验计算求得的光速，是如此精确地符合，这使我们难以回避如下推断：光是由介质的横波所形成，而这同一介质也是电现象和磁现象的起因。
— 马克士威， 论物理力线

参阅

• 《论法拉第力线》
• 《电磁场的动力学理论》
• 斐索-傅科仪
• 罗默测定光速
• 电磁波方程式
• 马克士威方程组
• 弯曲时空中的麦克斯韦方程组
• 马克士威应力张量
• 麦克斯韦方程组的历史

参考文献

• 《论物理力线》全文 1、2
• 马克士威, 詹姆斯, On physical lines of force 10, Philosophical Magazine: pp. 11–23, 1861, doi:10.1080/14786431003659180  引文格式1维护：冗余文本 (link)

进阶阅读

• Simpson, Thomas K., Maxwell on the electromagnetic field: a guided study, USA: Rutgers University Press, 1997, ISBN 9780813523637 
• Crease, Robert, The Great Equations: Breakthroughs in Science from Pythagoras to Heisenberg, illustrated, W. W. Norton & Company: pp. 132ff, 2008, ISBN 9780393062045  引文格式1维护：冗余文本 (link)
• Siegel, Daniel M., Innovation in Maxwell's Electromagnetic Theory: Molecular Vortices, Displacement Current, and Light, Cambridge University Press: 240, [2003], ISBN 9780521533294