七胞体
外观
| 部分的七胞体 | |
|---|---|
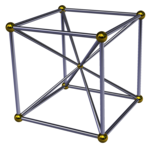 立方体锥体 (四维) |
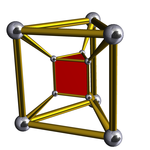 三角柱柱体 (四维) |
 三角四角柱体柱 (四维) |
 正七胞体 (六维) |
在几何学中,七胞体是指有七个胞或维面的多胞体。若七个胞都全等且都为正图形则为正七胞体。四维空间中不存在正七胞体,五维空间中也没有任何正七胞体存在,而在六维空间中,六维单纯形即是一种正七胞体,而八维以上的七胞体则退化为超球面镶嵌。
四维七胞体
[编辑]在四维空间中,七胞体为由7个多面体所组成的多胞体。四维空间中没有正七胞体,但有半正七胞体,例如立方体锥体[1]、三角四角柱体柱(或三角柱柱体)和双三角锥体的四维锥体等。
| 名称 | 考克斯特 施莱夫利 |
胞 | 图像 | 展开图 |
|---|---|---|---|---|
| 立方体锥体[2] | ( ) ∨ {4,3} | 1个立方体 6个四角锥 |
 |
|
| 三角四角柱体柱 | 3个立方体 4个三角柱 |
  |

| |
| 双三角锥体 的四维锥体 |
1个双三角锥 6个三角锥 |
五维七胞体
[编辑]在五维空间中,七胞体为由7个四维多胞体所组成的多胞体,例如正五胞体柱体、四面体柱体的五维锥体等。
六维七胞体
[编辑]在六维空间中,七胞体为由7个五维多胞体所组成的多胞体。其中,有一种正图形,即六维单纯形[3],其由7个正六胞体组成。其他的六维七胞体如正六胞体的六维空间锥体,即一个置于六维空间的五维正六胞体与其所在五维空间外取一点连至五维正六胞体所形成的图形。但其拓朴结构与正七胞体相同,因为其可以借由扭曲或改变正七胞体的高度而得。
七维以上的七胞体
[编辑]由于七维以上的空间要形成多胞体最少要有八个胞,例如七维空间的单纯形是一个八胞体,因此七维以上的七胞体多半是退化成超球面镶嵌(或堆砌)的图形,无法具有超体积,例如七维空间中以正七胞体为基底的多维面形。
参见
[编辑]参考文献
[编辑]- ^ Klitzing, Richard. 4D Segmentotopes. bendwavy.org. Klitzing, Richard. Segmentotope cubpy, K-4.26. bendwavy.org.
- ^ Richard Klitzing, Axial-Symmetrical Edge Facetings of Uniform Polyhedra (页面存档备份,存于互联网档案馆)
- ^ Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
