七胞體
外觀
| 部分的七胞體 | |
|---|---|
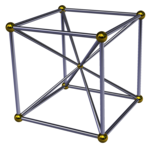 立方體錐體 (四維) |
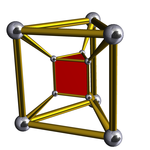 三角柱柱體 (四維) |
 三角四角柱體柱 (四維) |
 正七胞體 (六維) |
在幾何學中,七胞體是指有七個胞或維面的多胞體。若七個胞都全等且都為正圖形則為正七胞體。四維空間中不存在正七胞體,五維空間中也沒有任何正七胞體存在,而在六維空間中,六維單純形即是一種正七胞體,而八維以上的七胞體則退化為超球面鑲嵌。
四維七胞體
[編輯]在四維空間中,七胞體為由7個多面體所組成的多胞體。四維空間中沒有正七胞體,但有半正七胞體,例如立方體錐體[1]、三角四角柱體柱(或三角柱柱體)和雙三角錐體的四維錐體等。
| 名稱 | 考克斯特 施萊夫利 |
胞 | 圖像 | 展開圖 |
|---|---|---|---|---|
| 立方體錐體[2] | ( ) ∨ {4,3} | 1個立方體 6個四角錐 |
 |
|
| 三角四角柱體柱 | 3個立方體 4個三角柱 |
  |

| |
| 雙三角錐體 的四維錐體 |
1個雙三角錐 6個三角錐 |
五維七胞體
[編輯]在五維空間中,七胞體為由7個四維多胞體所組成的多胞體,例如正五胞體柱體、四面體柱體的五維錐體等。
六維七胞體
[編輯]在六維空間中,七胞體為由7個五維多胞體所組成的多胞體。其中,有一種正圖形,即六維單純形[3],其由7個正六胞體組成。其他的六維七胞體如正六胞體的六維空間錐體,即一個置於六維空間的五維正六胞體與其所在五維空間外取一點連至五維正六胞體所形成的圖形。但其拓樸結構與正七胞體相同,因為其可以藉由扭曲或改變正七胞體的高度而得。
七維以上的七胞體
[編輯]由於七維以上的空間要形成多胞體最少要有八個胞,例如七維空間的單純形是一個八胞體,因此七維以上的七胞體多半是退化成超球面鑲嵌(或堆砌)的圖形,無法具有超體積,例如七維空間中以正七胞體為基底的多維面形。
參見
[編輯]參考文獻
[編輯]- ^ Klitzing, Richard. 4D Segmentotopes. bendwavy.org. Klitzing, Richard. Segmentotope cubpy, K-4.26. bendwavy.org.
- ^ Richard Klitzing, Axial-Symmetrical Edge Facetings of Uniform Polyhedra (頁面存檔備份,存於網際網路檔案館)
- ^ Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
