序向邏輯電路
外觀
在數位電路理論中,序向邏輯電路是指電路任何時刻的穩態輸出不僅取決於當前的輸入,還與前一時刻輸入形成的狀態有關。這跟組合邏輯電路相反,組合邏輯的輸出只會跟目前的輸入成一種函數關係。換句話說,時序邏輯擁有儲存元件(記憶體)來存儲信息,而組合邏輯則沒有。
從時序邏輯電路中,可以建出兩種形式的有限狀態機:
時序邏輯因此被用來建構某些形式的電腦的記憶體,延遲跟儲存單元,以及有限狀態自動機。大部分現實的電腦電路都是混用組合邏輯跟時序邏輯。
特點
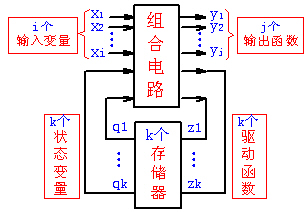
[編輯]- 功能特點:電路在某取樣周期內的穩態輸出Y(n),不僅取決於該取樣周期內的「即刻輸入X(n)」,而且還與電路原來的狀態Q(n)有關。(通常Q(n)記錄了以前若干周期內的輸入情況)
- 結構特點:除含有組合電路外,時序電路必須含有存儲信息的有記憶能力的電路:正反器、暫存器、計數器等。
時序電路框圖
[編輯]功能描述方法
[編輯]- 邏輯表達式
- 輸出方程組
- 驅動(激勵)方程組
- 狀態(次態)方程組
時序電路分類
[編輯]- 按「功能、用途」分為:
- 暫存器;
- 計數(分頻)器;
- 順序(序列)脈衝產生器;
- 順序脈衝檢測器;
- 碼組變換器;…
- 按各正反器的「動作特性」分為:
- 同步時序電路:電路中所有正反器的狀態變化同步進行。其時鐘方程:CP1= CP2=…= CPK= CP↓(或CP↑)。即:所有CP端聯在一起,由CP訊號同一有效沿觸發。
- 異步時序電路:
- 電路中根本沒有CP同步訊號。
- 各正反器不是用同一CP脈衝的同一有效沿觸發的。
- 摩爾(Moore)型和米里(Mealy)型
- 摩爾型:電路的輸出Yn,只取決於各正反器的輸出Q n,而與外輸入X n無關。即:Yn=F(Q n)。
- 米里型:電路的輸出Yn,不僅取決於各正反器的輸出Q n,而且還與外輸入X n有關。即:Yn=F(Q n,X n)。
- 「完全描述的」和「非完全描述的」含有K個狀態變量(K個正反器)的時序電路,最多可描述K個不同狀態。
- 若電路功能必須用個狀態來描述,則稱之為「完全描述的」(二進制的);
- 若只用個狀態中的一部分來描述,則稱之為「非完全描述的」(非二進制的)。
同步序向邏輯電路
[編輯]同步時序電路中所有存儲元件都在時鐘脈衝CP的統一控制下,用正反器作為存儲元件。幾乎現在所有的時序邏輯都是「同步邏輯」:有一個「時鐘」訊號,所有的內部記憶體('內部狀態')只會在時鐘的邊沿時候改變。在時序邏輯中最基本的儲存元件是正反器。
同步邏輯最主要的優點是它很簡單。每一個電路裡的運算必須要在時鐘的兩個脈衝之間固定的間隔內完成,稱為一個 '時鐘週期'。只有在這個條件滿足下(不考慮其他的某些細節),電路才能保證是可靠的。
同步邏輯也有兩個主要的缺點:
- 時鐘訊號必須要分佈到電路上的每一個正反器。而時鐘通常都是高頻率的訊號,這會導致功率的消耗,也就是產生熱量。即使每個正反器沒有做任何的事情,也會消耗少量的能量,因此會導致廢熱產生。
- 最大的可能時鐘頻率是由電路中最慢的邏輯路徑決定,也就是關鍵路徑。意思就是說每個邏輯的運算,從最簡單的到最複雜的,都要在每一個時脈的周期中完成。一種用來消除這種限制的方法,是將複雜的運算分開成為數個簡單的運算,這種技術稱為「流水線」。這種技術在微處理器中非常的顯著,用來幫處提升現今處理器的時鐘頻率。
描述同步序向邏輯電路的方法
[編輯]同步序向邏輯電路的存儲元件——正反器
[編輯]正反器是一種具有記憶能力、構成序向邏輯的基本單元電路。一個正反器能「存儲」一位二進制數位信息:「0」或「1」。
- 一個正反器有兩個穩定狀態:
- 「0」狀態:Q=0,=1;
- 「1」狀態:Q=1,=0。
- 正反器(FF)應具有以下功能:
- 在新數據輸入之前(無觸發訊號)時,正反器一直保持原來的狀態(原數據)不變。
- 輸入訊號觸發下,它能從一種狀態轉換為另一種狀態。即:FF能夠「接收」「保持」並「輸出」數位信息。
- 正反器(FF)的分類:
非同步邏輯(異步邏輯)
[編輯]非同步時序邏輯是循序邏輯的普遍本質,但是由於它的彈性關係,他也是設計上困難度最高的。最基本的儲存元件是閂鎖。閂鎖可以在任何時間改變它的狀態,依照其他的閂鎖訊號的變動,他們新的狀態就會被產生出來。非同步電路的複雜度隨著邏輯閘的增加,而複雜性也快速的增加,因此他們大部分僅僅使用在小的應用。然而,電腦輔助設計工具漸漸的可以簡化這些工作,允許更複雜的設計。
也可能建造出混合的電路,包含有同步的正反器和異步的閂鎖(它們都是雙穩態元件)。
參考文獻
[編輯]- Katz, R, and Boriello, G. Contemporary Logic Design. 2nd ed. Prentice Hall. 2005. ISBN 0-201-30857-6.
- Zvi Kohavi, Niraj K. Jha. Switching and Finite Automata Theory. 3rd ed. Cambridge University Press. 2009. ISBN 978-0-521-85748-2
- V. O. Vasyukevich. (2009). Asynchronous logic elements. Venjunction and sequention — 118 p.