无尺度网络

在网络理论中,无尺度网络(Scale-free network,或称无标度网络)是带有一类特性的复杂网络,其典型特征是在网络中的大部分节点只和很少节点连接,而有极少的节点与非常多的节点连接。这种关键的节点(称为“枢纽”或“集散节点”)的存在使得无尺度网络对意外故障有强大的承受能力,但面对协同性攻击时则显得脆弱。现实中的许多网络都带有无尺度的特性,例如因特网、金融系统网络、社会人际网络等等[1]。
源起[编辑]

无尺度网络的概念是随着对复杂网络的研究而出现的。“网络”其实就是数学中图论研究的图,由一群顶点以及它们之间所连的边构成。在网络理论中则换一套说法,用“节点”代替“顶点”,用“连结”代替“边”[2]:4[3]:9。复杂网络的概念,是用来描述由大量节点以及这些节点之间错综复杂的联系所构成的网络。这样的网络会出现简单网络中没有的特殊拓扑特性[3]:2。
自二十世纪60年代开始,对复杂网络的研究主要集中在随机网络上。随机网络,又称随机图,是指通过随机过程制造出的复杂网络。最典型的随机网络是保罗·埃尔德什和阿尔弗雷德·雷尼提出的ER模型。ER模型是基于一种“自然”的构造方法:假设有个节点,并假设每对节点之间相连的可能性都是常数。这样构造出的网络就是ER模型网络。科学家们最初使用这种模型来解释现实生活中的网络[2]:7-9。
ER模型随机网络有一个重要特性,就是虽然节点之间的连接是随机形成的,但最后产生的网络的度分布是高度平等的。度分布是指节点的度的分布情况。在网络中,每个节点都与另外某些节点相连,这种连接的数目叫做这个节点的度。在网络中随机抽取一个节点,它的度是多少呢?这个概率分布就称为节点的度分布[3]:11。
在一般的随机网络(如ER模型)中,大部分的节点的度都集中在某个特殊值附近,成钟形的泊松分布规律(见图3)[4]。偏离这个特定值的概率呈指数性下降,远大于或远小于这个值的可能都是微乎其微的[3]:11,就如一座城市中成年居民的身高大致的分布一样。然而在1998年,Albert-László Barabási、Réka Albert等人合作进行一项描绘万维网的研究时,发现通过超链接与网页、文件所构成的万维网网络并不是如一般的随机网络一样,有着均匀的度分布[5][6]。他们发现,万维网是由少数高连接性的页面串联起来的。绝大多数(超过80%)的网页只有不超过4个超链接,但极少数页面(不到总页面数的万分之一)却拥有极多的链接,超过1000个,有一份文件甚至与超过200万个其他页面相连。与居民身高的例子作类比的话,就是说大多数的节点都是“矮个子”,而却又有极少数的身高百丈的“巨人”。Barabási等人将其称为“无尺度”网络[5]。
描述与定义[编辑]

无尺度网络的特性,在于其度分布没有一个特定的平均值指标,即大多数节点的度在此附近。在研究这个网络的度分布时,Barabási等人发现其遵守幂律分布(也称为帕累托分布),也就是说,随机抽取一个节点,它的度是自然数的概率:
也就是说 的概率正比于 的某个幂次(一般是负的,记为)。因此越大, 的概率就越低。然而这个概率随增大而下降的“速度”是比较缓慢的:在一般的随机网络中,下降的速度是指数性的,而在无尺度网络中只是以多项式类的速度下降[3]:12。
在现实中许多大规模的无尺度网络中,度分布的值介于2与3之间[3]:14。在对数坐标系中,度分布将会是一条斜率介于-2至-3之间的直线[3]:12。如左下图中,横坐标为节点的度,从一直到;纵坐标为找到这样的节点的概率从一直到。最高度数的节点有882条连接。所有的蓝点大致成一条直线分布(绿色的直线)。
度-度相关性[编辑]

仅仅是将度分布的幂律分布作为无尺度网络的定义有其不够完善之处。由于幂律分布是方差可能无穷的高可变分布,对于度分布是同一个幂律分布的不同网络,其拓扑结构和特性可能存在巨大的差异。2005年,Lun Li和大卫·阿尔德森(David Alderson)等人在论文《迈向无标度图的理论》(Towards a Theory of Scale Free Graphs)中提出了一种补充性的标度性测度[7]。设为所有具有(依照幂律分布的)度分布的网络的集合,对于其中每一个网络,定义度-度相关数:
其中表示中所有连接的集合。根据排序原理,如果度数大的点之间相互连接的话,那么会比较大。设为最大的,那么定义度-度相关系数:
度-度相关系数介于0与1之间。越靠近1,则称此网络“无尺度”的,靠近0,则称是“富尺度”的。在此定义下,无尺度网络中的节点度数分布特征体现了自相似的性质,而凸显了“无尺度”的特征,与富尺度网络之间有相当的差异[7]。
例子[编辑]
不少现实中的网络结构都属于无尺度网络,或者有无尺度的特性。以下是一些无尺度网络的例子:
| 网络 | 节点 | 连接 |
|---|---|---|
| 电影演员网络[6] | 演员 | 出演同一部电影 |
| 万维网[6] | 网页 | 超链接 |
| 因特网[8] | 路由器 | 物理连接 |
| 蛋白质相互作用网络[9] | 蛋白质 | 蛋白质之间的相互作用关系 |
| 金融网络[10] | 金融机构 | 借贷关系 |
| 美国飞机航班网络[11] | 机场 | 飞机航线[12] |
BA模型[编辑]

Albert-László Barabási与Réka Albert在1999年的论文中提出了一个模型来解释复杂网络的无尺度特性,称为BA模型[6]。这个模型基于两个假设:
- 增长模式:不少现实网络是不断扩大不断增长而来的,例如互联网中新网页的诞生,人际网络中新朋友的加入,新的论文的发表,航空网络中新机场的建造等等。
- 优先连接模式:新的节点在加入时会倾向于与有更多连接的节点相连,例如新网页一般会有到知名的网络站点的连接,新加入社群的人会想与社群中的知名人士结识,新的论文倾向于引用已被广泛引用的著名文献,新机场会优先考虑建立与大机场之间的航线等等。
在这种假设下,BA模型的具体构造为:
- 增长:从一个较小的网络开始(这个网络有个节点,条边),逐步加入新的节点,每次加入一个。
- 连接:假设原来的网络已经有个节点()。在某次新加入一个节点时,从这个新节点向原有的个节点连出个连结。
- 优先连接:连接方式为优先考虑高度数的节点。对于某个原有节点(),将其在原网络中的度数记作,那么新节点与之相连的概率为:
这样,在经过次之后,得到的新网络有个节点,一共有条边[6][3]:27-28。
分析BA模型网络的渐近度分布(当节点数量很大时的度分布)主要有连续场理论、主方程法和速率方程法。这三种方法得到的渐近结果都是相同的。2001年,Béla Bollobás证明了在节点数量很大时,BA模型网络的度分布遵从的幂律分布[13][3]:29。之后,其它的无尺度网络模型也开始被提出。
其它无尺度模型[编辑]
BA模型成功的为无尺度网络找到了一个简单而合理的形成机制。然而,BA模型也有其自身的局限。例如,它只能描述的无尺度网络,对于真实网络的一些非幂律特征如指数截断(exponential cutoff)、小变量饱和(saturation of small variables)等无法描述[3]:33。因此,各种BA模型的推广、变化版本开始出现。Bollobás在2001年提出了线性弦图模型(LCD模型),允许节点自己与自己相连[14]。而后又出现了只允许重复连线而不允许自连线的模型[15]与不允许重复连线、自连线而是在选中的旧节点的邻域随机联线的模型[16]。
适应度模型[编辑]
在BA模型的制造过程中,人们发现,存在越久的节点具有越高的度数。然而,现实生活的网络中并非存在越久的元素就能有更多的联系。BA模型并没有包括“后起之秀”的现象[3]:33。于是,出现了基于BA模型的适应度模型。适应度模型主要是修正了优先连接的机制,对每个节点加上一个吸引因子,这样新节点的相连概率改正为:
局域世界演化模型[编辑]
另一种基于BA模型的推广版本是局域世界演化模型。这个模型假设每个新节点在引入时并不能在全域进行优先连接。比如说一家新上市的公司可能只会与同地区或同国家的公司展开贸易联系,居民搬入新社区时只会与同一幢楼的人开始认识等等。局域世界演化模型将BA模型优先连接的机制改为:新加入的节点时,先选择全部节点的一部分(随机选取的个节点)作为局域世界,然后再在局域世界中进行优先连接。模拟结果指出,当从变化到时,产生的网络从服从指数分布逐渐过渡到服从幂律分布[18]。
复制模型[编辑]
在BA模型中,度分布实际上是和增长的时间(或说增长次数)相关的,只是在十分大时近似于度分布。复制模型是一个与增长时间无关的模型。复制模型的做法是每次随机地“复制”一个原有的节点:即随机选定一个节点,再加入一个新节点,然后新节点按照与其它旧节点连接的方式与旧节点相连,最后与也相连[19]。
分层模型[编辑]
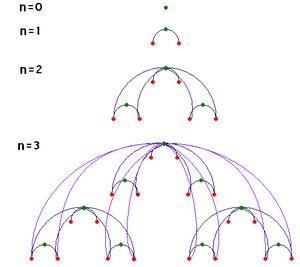
2001年,Barabási提出了第一个确定性的分层网络模型。这个模型是为了解释生物学中的代谢网络。分层模型的想法是从模体(motif)出发,通过自相似的层次叠加而得到复杂网络。这种思想类似于分数维图形。Barabási的模型是:
- 建立一个根节点,以及两个一级节点,并分别于根节点相连,这形成一个一级模体(右图6中n=1的阶段);
- 以一个一级模体作为根模体,再建立两个一级模体,将它们的一级节点(一共4个)与根模体的根节点相连,这样得到一个二级模体(右图6中n=2的阶段);
- 对二级模体重复前一步的操作(见右图n=3的阶段)。
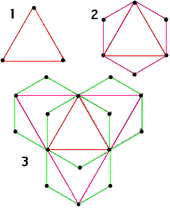
这样形成的网络是无尺度网络,Barabási算出它的[20]。后来有使用5节点4连结作为模体,得到,而4节点3连结作为模体得到,近似于代谢网络。需要注意的是此模型中不少度数是0概率的,所以需要使用补分布绕过。类似的确定性模型还有伪分形图(pseudofractal scale-free network)[21]以及阿波罗模型(Apollonian network)[22]。
无尺度网络的阿喀琉斯之踵[编辑]
2000年7月27日,《自然》杂志的封面文章标题是《因特网的阿喀琉斯之踵》(Achilles' Heel of the Internet)。阿喀琉斯是古希腊神话中的英雄,他出生后,他的母亲捏着他的脚踝将他浸泡在冥河中,从此他的身体刀枪不入,只有踵部没被浸到,是为其致命弱点。因此如今“阿喀琉斯之踵”常被用来称呼一个系统的致命缺陷[23]。这篇文章中从因特网的无尺度特性出发,探讨它对意外故障的承受能力。
假设在一个网络中移除一个节点,以及与其相关的连接,那么原网络中的其他点也可能受到影响:原本相连的两个节点可能不再相连;即使相连,从其中一处到另一处可能需要经过更多的路途。总的来说,网络的连通性降低了。文章比较了ER随机网络模型与BA模型在移除少量节点时对网络连通性的影响[24]。这个影响主要使用最大连通子图的大小与平均路径长度来衡量。在执行“随机攻击策略”,也就是在网络中随机地去除一些节点时,无尺度网络的比随机网络下降慢得多,的增长也缓慢得多。但是在执行“蓄意攻击策略”,也就是选择移除连接度最高的节点时,则会得到相反的结果[24]。受到随机攻击的随机图会分裂成几个较小的子图,而无尺度网络则有很大概率保持连通;然而面对蓄意攻击(或称协同攻击)时,只需要移除5-10%的高于5度的节点,就能彻底瘫痪无尺度网络[3]:31-33。
流行病临界值[编辑]
流行病或网络病毒在复杂网络中的传播也是复杂网络研究的方向之一。在均匀网络如ER模型随机网络或小世界网络中,如果考虑易感(S)→感染(I)→易感(S)的SIS模型,那么存在一个与网络特性相关的临界值,当有效传播率高于这个临界值的时候,传染病会在网络中传播并稳定在某个恒定密度上(激活相态)。而当有效传播率低于这个临界值时,传染病会很快逐渐消亡(吸收相态)[3]:73-74。对于无尺度网络,由于度分布不均匀,临界值比较小。对于BA模型,临界值为0。也就是说,只要有效传播率大于0,病毒就能有效传播并达到稳定[25]。而对于有限规模的无标度网络,临界值大于0,但会在均匀网络的十分之一左右。因此,无标度网络对于病毒传播的抵抗性较均匀网络脆弱得多[26]。
由于无尺度网络应对流行病感染的脆弱性,人们提出不同的免疫策略来弥补。主要研究的免疫策略有三种:随机免疫、选择免疫与熟人免疫[3]:79。
随机免疫[编辑]
随机免疫是在网络中随机抽取一部分节点进行免疫。研究表明,采取这种策略的话,需要对网络中几乎所有的节点都进行免疫才能保证最终消灭传染病[3]:79。
选择免疫[编辑]
选择免疫是在网络中抽取度最大的节点进行免疫。就BA模型而言,采取这种策略的话,即使有效传播率变化,也可以只免疫很小一部分节点就保证消灭传染病[3]:79。
熟人免疫[编辑]
由于选择免疫需要知道全局节点的度数情况,才能找到度数最大节点进行免疫,这在面对互联网等庞大的复杂网络时会导致难以操作。熟人免疫采取的是随机抽取一部分节点,然后对每个节点随机选一个与之相连的“邻居”节点来进行免疫。由于在无尺度网络中,度大的节点可以与非常多的节点相连,因此选择“邻居”免疫的话,碰到度大节点的概率会比碰到度小节点的概率大得多。所以熟人免疫要比随机免疫有效得多,只略差于选择免疫[27][3]:79。
同步性[编辑]
音乐会或歌剧完场时,台下的观众不间断地鼓掌。在很短几次后,鼓掌的频率就会变得同步。这种现象显示出网络的同步性。研究表明,网络动力系统的同步性取决于节点动力系统的特性,节点的耦合方式与网络的结构。对于BA模型网络,节点数的增加不会降低网络同步的稳定性。而面对随机攻击和蓄意攻击,BA模型网络的同步性与连通性表现出相同的特征:对于随机攻击承受性强,而对蓄意攻击则显得脆弱[3]:79。
参考来源[编辑]
- ^ 張皓。「《灌園先生日記》中家族社會網絡之分析研究(1927—1932)」。碩士論文,國立彰化師範大學歷史學研究所,2024。
- ^ 2.0 2.1 Richard Durrett. Random graph dynamics. Cambridge University Press. 2007. ISBN 978-0-521-86656-9 (英语).
- ^ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 3.10 3.11 3.12 3.13 3.14 3.15 3.16 3.17 汪小帆,李翔,陈关荣. 《复杂网络理论及其应用》. 清华大学出版社. 2006. ISBN 9787302125051 (中文).
- ^ Statistical analysis of network data: methods and models, p.157
- ^ 5.0 5.1 《科学美国人》中文版2003年7月. 无尺度网络. 集智集团. [2011-07-04]. (原始内容存档于2021-03-11).
- ^ 6.0 6.1 6.2 6.3 6.4 Albert-László Barabási, Réka Albert. Emergence of Scaling in Random Networks (PDF). Science: 509–512. [2011-07-09]. doi:10.1126/science.286.5439.509. (原始内容存档 (PDF)于2021-09-23).
- ^ 7.0 7.1 Lun Li, David Alderson, Reiko Tanaka, John C. Doyle, Walter Willinger. Towards a Theory of Scale-Free Graphs: Definition, Properties, and Implications (PDF). Internet Mathematics: 431–523. [2011-07-09]. doi:10.1080/15427951.2005.10129111. (原始内容存档 (PDF)于2021-09-23) (英语).
- ^ Ye Xu and Wen-bo Zhang. A Power-Law Approach on Router-Level Internet Macroscopic Topology Modeling. Advances in Intelligent and Soft Computing: 1471–1479. doi:10.1007/978-3-642-03664-4_156.
- ^ L.Giot; et al. A Protein Interaction Map of Drosophila melanogaster (PDF). Science: 1727–1736. [2011-07-11]. doi:10.1126/science.1090289. (原始内容 (PDF)存档于2011-01-12).
- ^ Rama Cont , Amal Moussa, Edson Bastos e Santos. Network Structure and Systemic Risk in Banking Systems (PDF). SSRN.
- ^ 中国和印度的国内航班网络则更适合用小世界网络刻画
- ^ Sheila R.Conway. scale-free networks and commercial air carrier transportation in the United States (PDF). 24th international congress of the aeronautical sciences.[永久失效連結]
- ^ Bollobás, B.; Riordan, O.; Spencer, J.; Tusnády, G. The degree sequence of a scale-free random graph process. Random Structures and Algorithms. 2001, 18 (3): 279–290. MR 1824277. doi:10.1002/rsa.1009.
- ^ Béla Bollobás, Oliver Riordan, Joel Spencer, Gábor Tusnády. The degree sequence of a scale-free random graph process. Random structures & algorithms: 279––290. doi:10.1002/rsa.1009 (英语).
- ^ S.N.Dorogovtsev, J.F.Mendes , A.N.Samukhin. Structure of growing networks with preferential linking. Physical review lettres. doi:10.1103/PhysRevLett.85.4633 (英语).
- ^ Holme P;Kim B J. Growing scale free networks with tunable clustering. Physical review E. doi:10.1103/PhysRevE.65.026107 (英语).
- ^ G. Bianconi ;A.L.Barabasi. Bose-Einstein condensation in complex networks. Physical review letters. doi:10.1103/PhysRevLett.86.5632 (英语).
- ^ Qin, Sen; Dai, Guan-Zhong. A new local-world evolving network model. Chinese Physics B: 383–390. doi:10.1088/1674-1056/18/2/001 (英语).
- ^ R. Kumar, P. Raghavan, S. Rajagopalan, D. Sivakumar, A. Tomkins, E. Upfal. Stochastic models for the Web graph. IEEE Comput. Soc: 57–65. doi:10.1109/SFCS.2000.892065 (英语).
- ^ Albert-Laszlo Barabasi, Erzsebet Ravasz, Tamas Vicsek. Deterministic Scale-Free Networks. Physica review A: 559–564. doi:10.1016/S0378-4371(01)00369-7 (英语).
- ^ S.N. Dorogovtsev, A.V. Goltsev, J.F.F. Mendes. Pseudofractal Scale-free Web. Physica review E. doi:10.1103/PhysRevE.65.066122 (英语).
- ^ Jose S. Andrade Jr., Hans J. Herrmann, Roberto F. S. Andrade, Luciano R. da Silva. Apollonian networks. Physica review lettres. doi:10.1103/PhysRevLett.94.018702 (英语).
- ^ 据苏联俄罗斯联邦教育部国家教科书出版社列宁格勒全社1961年俄文版译. 神话辞典. 商务印书馆. 1985.第19页.
- ^ 24.0 24.1 Réka Albert, Hawoong Jeong, Albert-László Barabási. Error and attack tolerance of complex networks. Nature. 27 July 2000, 406 (6794): 378–382 [2011-07-09]. doi:10.1.1.33.2606/nature.406.2115.378. (原始内容存档于2021-03-01) (英语).
- ^ Romualdo Pastor-Satorras, Alessandro Vespignani. Epidemic Spreading in Scale-Free Networks (PDF). Physical review lettres: 3200–3203. [2011-07-09]. doi:10.1103/PhysRevLett.86.3200. (原始内容存档 (PDF)于2021-09-23) (英语).
- ^ Romualdo Pastor-Satorras, Alessandro Vespignani. Epidemic dynamics in finite size scale-free networks (PDF). Physical review E. [2011-07-09]. doi:10.1103/PhysRevE.65.035108. (原始内容存档 (PDF)于2021-03-04) (英语).
- ^ Reuven Cohen, Shlomo Havlin, Daniel ben-Avraham. Efficient Immunization Strategies for Computer Networks and Populations (PDF). Physical review lettres. [2011-07-09]. doi:10.1103/PhysRevLett.91.247901. (原始内容存档 (PDF)于2021-03-04) (英语).
- Eric D. Kolaczyk. Statistical analysis of network data: methods and models. Springer; 1 edition. 2009. ISBN 978-0387881454 (英语).
- Richard Durrett. Random graph dynamics. Cambridge University Press. 2007. ISBN 978-0-521-86656-9 (英语).
















































