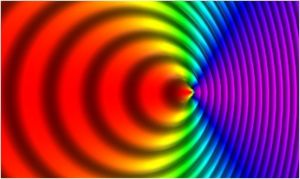
 一个光源向右移动,速度为0.7c。频率在右面较高,在左面较低。
一个光源向右移动,速度为0.7c。频率在右面较高,在左面较低。
相對論性多普勒效應描述了光因為波源與觀察者的相對運動關係(一如尋常版的多普勒效應)而有的頻率(以及波長)上的變化,而在這裡又多考慮了狹義相對論帶來的效應。
相對論性多普勒效應和非相對論性版本的多普勒效應有許多不同之處,例如其方程式納入了狹義相對論中的時間展長效應。這些方程式描述了所觀察到的完全頻率差值,並具有相對論要求的洛侖茲對稱性。
機制(一個簡單例子)[编辑]
假設觀察者(Observer)與波源(Source)是以一相對速度 彼此遠離,並從波源的參考系來考慮這個問題。
彼此遠離,並從波源的參考系來考慮這個問題。
當某一波前抵達觀察者處,則下一個最接近的波前距離觀察者有 (其中
(其中 是波長、
是波長、 是波源所發出的原始光波頻率、
是波源所發出的原始光波頻率、 是光速)。由於波前移動速度(即光波移動速度)為
是光速)。由於波前移動速度(即光波移動速度)為 而觀察者遠離速度為
而觀察者遠離速度為 ,觀察者接收一個完整的波(或經歷兩個波前)需歷時:
,觀察者接收一個完整的波(或經歷兩個波前)需歷時:

當物體以相對高速移動時,需考慮相對論的時間膨脹效應,故觀察者測量到的時間會是:

其中 ,所以觀察者測量到的頻率是:
,所以觀察者測量到的頻率是:
 。
。
當運動沿著波動傳遞路線[编辑]
若觀察者與波源正以速度 彼此遠離,則觀察到的頻率
彼此遠離,則觀察到的頻率 會與波源發出的頻率
會與波源發出的頻率 相異,關係式可寫作:
相異,關係式可寫作:

其中 是真空中光速。
是真空中光速。
相應的波長關係式則可寫作:

所導致的紅移 可寫作
可寫作

在非相對論極限下,亦即當 ,近似式可寫作:
,近似式可寫作:

註:此段落所假設的是觀察者和波源互相「遠離」。若他們是互相「接近」,則 需設為負值。
需設為負值。
當運動沿著任意方向[编辑]
若從觀察者參考系來看,波源以速度 以及相對於從觀察者到波源方向呈一個角度
以及相對於從觀察者到波源方向呈一個角度 (光從參波源發射到觀察者方向與波源速度的夾角)遠離,則頻率變化為
(光從參波源發射到觀察者方向與波源速度的夾角)遠離,則頻率變化為

其中
然而,若角度 是在波源參考系量測到的(光從參波源發射到觀察者方向於觀察者速度的夾角),則表示式為
是在波源參考系量測到的(光從參波源發射到觀察者方向於觀察者速度的夾角),則表示式為

在非相對論極限下:
 。
。
相關條目[编辑]
外部連結[编辑]























