侧锥三角柱
 | ||
| 类别 | 约翰逊多面体 J48 - J49 - J50 | |
|---|---|---|
| 识别 | ||
| 名称 | 侧锥三角柱 | |
| 参考索引 | J49 | |
| 鲍尔斯缩写 | autip | |
| 性质 | ||
| 面 | 8 | |
| 边 | 13 | |
| 顶点 | 7 | |
| 欧拉特征数 | F=8, E=13, V=7 (χ=2) | |
| 组成与布局 | ||
| 面的种类 | 6个三角形 2个正方形 | |
| 顶点图 | 2个(3.42) 1个(34) 4个(33.4) | |
| 对称性 | ||
| 对称群 | C2v群 | |
| 特性 | ||
| 凸 | ||
| 图像 | ||
| ||
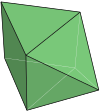
侧锥三角柱(英文:Augmented triangular prism)属于约翰逊多面体之一,索引为J49[1],可由一个正四角锥(J1)和正三角柱分别以底面和侧面相互黏合而成[1]。它在外观上与异相双三角柱(J26)十分相像,唯一的差别在于前者以正四角锥取代了后者的一个三角柱。它与二侧锥三角柱(J50)和三侧锥三角柱(J51)有着类似的构造。约翰逊多面体是凸多面体,面皆由正多边形组成但不属于均匀多面体,共有92种。这些立体最早在1966年由诺曼·约翰逊(Norman Johnson)命名并给予描述[2]。
性质
[编辑]侧锥三角柱共由8个面、13条边和7个顶点组成[3][4][5]。在其8个面中,有6个正三角形面和2个正方形面。侧锥三角柱可以视为三角柱与2个正四角锥的组合[6]:86,因此侧锥三角柱的6个三角形面又可以分成两组,一组为侧锥的侧面,有4个正三角形,以及三角柱的两个三角形底面。在其7个顶点中,有1个顶点是4个三角形的公共顶点[5],在顶点图中可以用[34]来表示[7]、还有4个顶点是3个三角形和1个正方形的公共顶点[5],在顶点图中可以用[33,4]来表示[7]、剩下的2个顶点是1个三角形和2个正方形的公共顶点[5],在顶点图中可以用[3,42]来表示[7]。
二面角
[编辑]侧锥三角柱有5种二面角,分别是2种三角形与三角形的二面角、2种三角形与正方形的二面角以及1种正方形与正方形的二面角。[7]其中正方形与正方形的二面角为60度。[7]
- 正方形正方形
2种三角形与三角形的二面角分别为侧锥与三角柱交会处的三角形与三角形的二面角以及侧锥上的三角形与三角形的二面角。
- 其中,侧锥与三角柱交会处的三角形与三角形的二面角角度为负三分之二平方根的反余弦值,角度约为144.7度:[7]
- 而,侧锥与三角柱交会处的三角形与三角形的二面角角度为负三分之一的反余弦值,约为109.471度:[7]
2种三角形与正方形的二面角分别为侧锥与三角柱交会处的三角形与正方形的二面角以及三角柱上的三角形与正方形的二面角。
顶点座标
[编辑]侧锥三角柱的顶点座标为:[7]
相关多面体
[编辑]侧锥三角柱是1个侧面被四角锥取代的三角柱。其他也是侧面被取代的三角柱结构有二侧锥三角柱和三侧锥三角柱。[6]:86
-
侧锥三角柱
侧锥三角柱是底面为三角形之柱体对应的侧锥柱体,其他的侧锥柱体有:
| 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|
|

|

|

|
|
| 侧锥三角柱 | 侧锥四角柱 | 侧锥五角柱 | 侧锥六角柱 | 侧锥七角柱 |
参见
[编辑]参考文献
[编辑]- ^ 1.0 1.1 Weisstein, Eric W. (编). Augmented triangular prism. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
- ^ David I. McCooey. Johnson Solids: Augmented Triangular Prism. [2022-09-07]. (原始内容存档于2022-09-10).
- ^ The Augmented Triangular Prism. qfbox.info. [2022-09-08]. (原始内容存档于2022-12-31).
- ^ 5.0 5.1 5.2 5.3 Augmented Triangular Prism. polyhedra.tessera.li. [2022-09-10]. (原始内容存档于2022-09-10).
- ^ 6.0 6.1 Rajwade, A.R. Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. 2001. ISBN 9789386279064.
- ^ 7.00 7.01 7.02 7.03 7.04 7.05 7.06 7.07 7.08 7.09 Richard Klitzing. Augmented Triangular Prism, autip. bendwavy.org. [2022-09-08]. (原始内容存档于2022-11-14).













