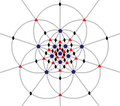
多面体群

几何学中，多面体群指柏拉图立体的对称群。

群

多面体群共三个：

• 12阶四面体群，正四面体的旋转对称群。它与A₄同构。
  • T的共轭类是：
    • 恒等
    • 4 × 旋转 120°，3阶，顺时针
    • 4 × 旋转 120°，3阶，逆时针
    • 3 × 旋转 180°，2阶
• 24阶八面体群，立方体和正八面体的旋转对称群。它与S₄同构。
  • O的共轭类是：
    • 恒等
    • 6 × 围绕顶点旋转 ±90°，4阶
    • 8 × 围绕三角形中心旋转 ±120°，3阶
    • 3 × 围绕顶点旋转 180°，2阶
    • 6 × 围绕边缘中点旋转 180°，2阶
• 60阶二十面体群，正十二面体和正二十面体的旋转对称群。它与A₅同构。
  • I的共轭类是：
    • 恒等
    • 12 × 旋转 ±72°，5阶
    • 12 × 旋转 ±144°，5阶
    • 20 × 旋转 ±120°，3阶
    • 15 × 旋转 180°，2阶

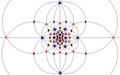
对于全反射群，以上的对称性加倍，分别为24、48、120阶，分别有6、9 和15 个反射镜面。八面体对称群[4,3]可以看作是四面体对称群 [3,3] 的6个反射镜面和二面体群Dih₂[2,2] 的3个反射镜面的并集。五角十二面体对称性是四面体对称性的另一种加倍。

完全四面体对称的共轭类T_d≅S₄是：

• 恒等
• 8 × 旋转 120°
• 3 × 旋转 180°
• 6 × 通过两个旋转轴在平面内进行反映
• 6 × 旋转-反映 90°

五角十二面体对称性T_h的共轭类包括T的共轭类，其中两个4阶类组合在一起，并且每个类都具有反演：

• 恒等
• 8 × 旋转 120°
• 3 × 旋转 180°
• 反演
• 8 × 旋转-反映 60°
• 3 × 平面反映

全八面体群O_h ≅ S₄ × C₂的共轭类是：

• 反演
• 6 × 旋转-反映 90°
• 8 × 旋转-反映 60°
• 垂直于 4 次轴的平面中的 3 × 反射
• 垂直于 2 次轴的平面中的 6 × 反射

完全二十面体对称 I_h ≅ A₅ × C₂的共轭类 ，还包括每个具有反演的：

• 反演
• 12 × 旋转-反映 108°， 10阶
• 12 × 旋转-反映 36°，10阶
• 20 × 旋转-反映 60°，6阶
• 15 × 旋转-反映，2 阶

手性多面体群

手性多面体基团

名称/熊夫利斯（Schönflies）记号 （轨型符号 )	考克斯特符号	阶	抽象结构	旋转轴 #度	图表
					正交	立体
T(332)	[3,3]+	12	A4	4332
Th (3*2)	[4,3+]	24	A4 ×2	433*2
O (432)	[4,3]+	24	S4	344362
I (532)	[5,3]+	60	A5	65103152

全多面体群

全多面体群

熊夫利斯（Schönflies）记号 （轨型符号轨型符号)	考克斯特符号	阶	抽象 结构	考克斯特数字（H）	镜面 (h)	镜像图
						正交	立体
A3 Td (*332)	[3,3]	24	S4	4	6
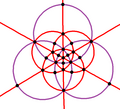
B3 Oh (*432)	[4,3]	48	S4 ×2	8	3 6
H3 Ih (*532)	[5,3]	120	5 ×2	10	15

参见

• 威霍夫符号
• 球对称群列表

参考文献

• Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973. (The Polyhedral Groups. §3.5, pp. 46–47)

外部链接

• 埃里克·韦斯坦因. PolyhedralGroup. MathWorld.