倒單擺

平衡台車是簡單的機械人系統。台車中有伺服機構，監控桿子的角度，利用讓台車來回移動時來維持直桿直立，上面的酒杯可以觀察直桿是否有大幅震蕩或是傾斜角度過大

倒單擺是質心在其樞紐點以上的擺。倒單擺在力學上無法穩定平衡，在沒有額外控制時，倒單擺會倒下。若利用控制系統控制桿的角度，在桿開始要倒下時調整質心位置，讓桿子不會倒下，可以維持倒單擺的平衡。倒單擺是動力學及控制理論中的經典問題，常用來測試不同的控制策略。倒單擺常以樞紐點在台車上的方式來呈現，如圖所示。這稱為「台車和桿子」。大部份的應用會限制單擺只有一個自由度，固定擺的旋轉軸。一般的單擺在重物在樞紐點下方時會平衡，倒單擺在其本質上就無法自行平衡，需要透過外在控制才能平衡。外在控制平衡的作法可以在樞紐點加力矩，或是讓樞紐點水平移動，再透過回授系統來使倒單擺平衡，改變質量相對樞紐點轉動的速度，或是讓樞紐點在垂直方向晃動。像人用手設法平衡倒立的掃帚，就是人工平衡倒單擺的例子。

簡介

單擺的重物在樞紐點下方時，即為系統的穩定平衡點。單擺不受外在力矩時可以維持不動，若讓單擺重物偏離平衡位置，放開後重力會產生力矩使單擺回到平衡點。倒單擺旳重物在樞紐點上方，會用剛體的桿子支持重物，位置恰好和穩定平衡點相差180度，是不穩定平衡點：倒單擺在不受外在力矩時可以維持不動，但若只要有一點偏差，重物就會偏離平衡，而重力產生的力矩會使單擺偏離平衡點，因此最後倒單擺會倒下。

為了要使單擺在倒單擺的位置下可以維持平衡，可以使用控制系統，監控倒單擺的角度，在倒單擺開始要倒下時加以施加力或是力矩，使它往反方面移動，設法讓它平衡。倒單擺是動力學及控制理論中的經典問題，常用來測試不同的控制演算法（例如PID控制器、狀態空間、類神經網路、模糊控制、遺傳算法等）。此問題的一些變化包括有多個桿、由倒單擺改為台車及倒單擺系統（台車和桿子），在蹺蹺板上平衡台車及倒單擺系統。倒單擺和火箭或是飛彈導引系統有關，其重心位在阻力中心的後方，因此在空氣力學上會不穩定。用伺服機構平衡台車及倒單擺系統就可以對此問題有一些理解，或是徒手設法平衡倒立的掃帚也可以。利用自平衡的個人運輸工具即可解決此問題，例如賽格威、自平衡滑行車及自平衡單輪車。

另外有一種可以使倒單擺穩定，而且不需回授或是控制系統的方式，是將倒單擺的樞紐快速上下震盪，這稱為是卡皮察擺。若振盪的加速度及振幅夠大，倒單擺會以一種反直覺的方式從擾動中恢復平衡。若樞鈕是以簡諧運動的方式運動，則倒單擺的運動可以用馬丟函數來描述。

運動方程

倒單擺的運動方程和單擺運動的限制條件有關。倒單擺會依照其運動組態的不同，有不同的運動方程。

固定樞紐點

若倒單擺的樞紐點固定無法移動，其運動方程會類似一般的單擺，但符號會有些不同。以下的運動方程假設沒有摩擦力，在運動時也沒有阻力，桿為剛體，沒有質量，而且運動限制在二維空間內。

${\ddot {\theta }}-{g \over \ell }\sin \theta =0$

其中${\ddot {\theta }}$是擺的角加速度，$g$是地球表面的標準重力，$\ell$是擺的長度，而$\theta$是擺相對平衡位置的角度。

也可以計算角加速度如下：

${\ddot {\theta }}={g \over \ell }\sin \theta$

倒單擺的角加速度會使擺遠離不穩定平衡的垂直位置，角加速度和長度成反比。長的倒單擺倒下的速度會比較慢。

用力矩及轉動慣量來推導

假設倒單擺的擺由質量為$m$的質點，接在長度為$\ell$的剛體無質量桿上，擺的另一端是固定的樞紐點。

系統的淨力矩會等於轉動慣量和角加速度的乘積：

${\boldsymbol {\tau }}_{\mathrm {net} }=I{\ddot {\theta }}$

淨力矩是由重力產生的力矩：

${\boldsymbol {\tau }}_{\mathrm {net} }=mg\ell \sin \theta \,\!$

其中$\theta \$是擺相對平衡位置的角度。

所得的方程式為：

$I{\ddot {\theta }}=mg\ell \sin \theta \,\!$

點質點的轉動慣量公式為：

$I=mR^{2}$

在倒單擺的例子中，半徑為擺的長度$\ell$。

將轉動慣量用$I=m\ell ^{2}$來表示

$m\ell ^{2}{\ddot {\theta }}=mg\ell \sin \theta \,\!$

等號兩邊同除$\ell ^{2}$，可得：

${\ddot {\theta }}={g \over \ell }\sin \theta$

台車上的倒單擺

台車上倒單擺的圖，假設桿沒有質量，台車質量及擺的質量分別是M和m，桿的長度假設是$\ell$

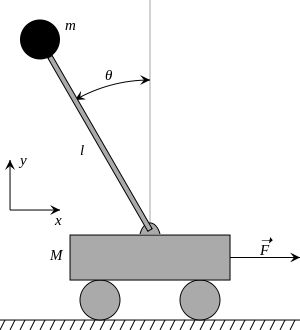
台車上的倒單擺包括質量為$M$的台車,上面有可以轉動的桿，頂端有質量為$m$的重物，台車的運動方向受到限制，只能在一個方向進行線性運動。

拉格朗日方程

可以用拉格朗日力學推導運動方程。以右側的圖為準，其中的$\theta (t)$是長度為$l$的擺相對於垂直線的角度，而作用力是重力以及x方向的外力F。定義$x(t)$是台車的位置，系統的拉格朗日量$L=T-V$為：

$L={\frac {1}{2}}Mv_{1}^{2}+{\frac {1}{2}}mv_{2}^{2}-mg\ell \cos \theta$

其中$v_{1}$是台車速度，$v_{2}$是點狀質量$m$的速度。 $v_{1}$及$v_{2}$可以用x和$\theta$來表示，其作法是將速度寫成位置的一階導數：

$v_{1}^{2}={\dot {x}}^{2}$

$v_{2}^{2}=\left({\frac {d}{dt}}{\left(x-\ell \sin \theta \right)}\right)^{2}+\left({\frac {d}{dt}}{\left(\ell \cos \theta \right)}\right)^{2}$

簡化$v_{2}$的式子可得：

$v_{2}^{2}={\dot {x}}^{2}-2\ell {\dot {x}}{\dot {\theta }}\cos \theta +\ell ^{2}{\dot {\theta }}^{2}$

拉格朗日量為：

$L={\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}-m\ell {\dot {x}}{\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}-mg\ell \cos \theta$

運動方程為：

${\frac {\mathrm {d} }{\mathrm {d} t}}{\partial {L} \over \partial {\dot {x}}}-{\partial {L} \over \partial x}=F$

${\frac {\mathrm {d} }{\mathrm {d} t}}{\partial {L} \over \partial {\dot {\theta }}}-{\partial {L} \over \partial \theta }=0$

替代式子中的$L$，並且簡化，可以得到倒單擺的運動方程：

$\left(M+m\right){\ddot {x}}-m\ell {\ddot {\theta }}\cos \theta +m\ell {\dot {\theta }}^{2}\sin \theta =F$

$\ell {\ddot {\theta }}-g\sin \theta ={\ddot {x}}\cos \theta$

上述式子是非線性的，不過因為目標是維持倒單擺直立，方程式可以在$\theta \approx 0$附近線性化。

牛頓第二運動定律

若用牛頓第二運動定律求解此問題，可以得到單擺和台車各部份的作用力，每一個物體都有二個方程式，分別是x方向及y方向。台車的運動方程如下，等號左邊是合力，等號右邊是質量及加速度。

$F-R_{x}=M{\ddot {x}}$

$F_{N}-R_{y}-Mg=0$

上式中$R_{x}$和$R_{y}$是樞紐點上的作用力，$F_{N}$是台車受到的正向力。第二個式子只和垂直的作用力有關，因此可以用來求解正向力。第一個式子可以用求解水平的作用力。為了完成以上的方程，需要計算擺的加速度，若在慣性坐標下，點質量的位置是

${\vec {r}}_{P}=(x-\ell \sin \theta ){\hat {x}}_{I}+\ell \cos \theta {\hat {y}}_{I}$

在慣性坐標下，對時間取二階微分，即可得到加速度。

${\vec {a}}_{P/I}=({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta ){\hat {x}}_{I}+(-\ell {\dot {\theta }}^{2}\cos \theta -\ell {\ddot {\theta }}\sin \theta ){\hat {y}}_{I}$

因此，用牛頓第二運動定律求解時，可以列出x方向及y方向的式子。注意給擺的反作用力是正的，給台車的是負的。這是因為牛頓第三運動定律的結果。

$R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )$

$R_{y}-mg=m(-\ell {\dot {\theta }}^{2}\cos \theta -\ell {\ddot {\theta }}\sin \theta )$

第一個方程式提供了一個在未知外力$F$時，可以計算水平反作用力的方式。可以用第二式求解垂直作用力，再將第一式的$R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )$用$F-R_{x}=M{\ddot {x}}$取代，可得

$\left(M+m\right){\ddot {x}}-m\ell {\ddot {\theta }}\cos \theta +m\ell {\dot {\theta }}^{2}\sin \theta =F$

可以觀察到這個式子和拉格朗日方程的結果完全一樣。為了得到第二式，需要將擺的運動方程和始終和擺垂直的單位向量進行點積，結果會列為物體座標（B）下的X軸。在慣性座標（I）下，向量可以用以下簡單的二維坐標轉換來表示

${\hat {x}}_{B}=\cos \theta {\hat {x}}_{I}+\sin \theta {\hat {y}}_{I}$

擺的運動方程可以寫作向量的形式，為$\sum {\vec {F}}=m{\vec {a}}_{P/I}$。在兩側和${\hat {x}}_{B}$作點積，可得以下等式的左邊（注意轉置後點積的結果相同）

$({\hat {x}}_{B})^{T}\sum {\vec {F}}=({\hat {x}}_{B})^{T}(R_{x}{\hat {x}}_{I}+R_{y}{\hat {y}}_{I}-mg{\hat {y}}_{I})=({\hat {x}}_{B})^{T}(R_{p}{\hat {y}}_{B}-mg{\hat {y}}_{I})=-mg\sin \theta$

上式中用到了在物體移動方向為準的反作用力分量，以及慣性座標下反作用力分量之間的關係。假設中有假設桿無質量，因此桿無法給予垂直桿子的力。慣性座標下的反作用力可以寫成$R_{p}{\hat {y}}_{B}$，強調桿只能提供和桿平行的力。因此會產生另外一個方程，可以求解桿上的張力

$R_{p}={\sqrt {R_{x}^{2}+R_{y}^{2}}}$

等式的右邊也可以用將擺的力加速度和${\hat {x}}_{B}$點積的方式計算，結果（經過一些簡化）如下

$m({\hat {x}}_{B})^{T}({\vec {a}}_{P/I})=m({\ddot {x}}\cos \theta -\ell {\ddot {\theta }})$

合併左式及右式，並且除以m可得

$\ell {\ddot {\theta }}-g\sin \theta ={\ddot {x}}\cos \theta$

此結果也和拉格朗日方程的結果相同，使用牛頓運動定律的好處是知道所有的反作用力，可以確定擺和台車不會因為受力過大而損毀。

穩定台車倒單擺的方式

穩定台車倒單擺的方式，可以簡述為下三點。

台車和倒單擺的例子中，簡單的穩定控制系統

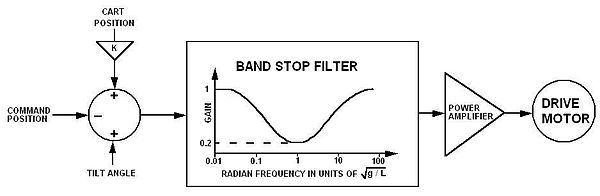
1. 若直桿往右傾斜，台車需要往右加速，反之亦然。
2. 台車相對軌道中心的位置$x$穩定的方式是是將null angle由台車的位置來進行調整，也就是null angle $=\theta +kx$，其中$k$是小的數值。因此桿會輕微的向軌道中心傾斜，若其角度恰好垂直的話，就會穩定在軌道中心。傾斜感測器或是軌道斜率的誤差（本來會造成不穩定的效應）都會變成穩定的位置偏移量，另外增加的偏移量則是為了位置控制。
3. 正常的擺單擺在角頻率為$\omega _{p}={\sqrt {g/\ell }}$時會共振。為了避免不受控的晃動，樞紐點需要抑制在共振頻率$\omega _{p}$附近的頻率響應。倒單擺也需要類似的帶拒濾波器才能達到穩定。

由於null angle調整策略的結果，正回授的結果為正，若擺突然往右移動，會讓平台的初始速度往左，但之後會往右，以讓倒單擺重新平衡。擺的不穩定性以及正位置回授的不穩定性交互作用，以產生一個穩定的系統，這是倒單擺穩定問題的特徵，也是在數學分炘上有趣而有挑戰性的地方。

建構卡皮察擺的作法。馬達在高速時旋轉曲柄，曲柄使槓桿上下擺動，槓桿的末端連接倒單擺

卡皮察擺

倒單擺若在上下振動的平台上，有可能可以在不受控的情形下穩定，最早研究這種倒單擺的是俄國科學家彼得·列昂尼多維奇·卡皮察，因此這種擺也稱為卡皮察擺。在無質量垂直振盪平台上的擺，其運動方程推導方式類似台車上的單擺，點質點的位置為：

$\left(-\ell \sin \theta ,y+\ell \cos \theta \right)$

一次微分後可以得到速度：

$v^{2}={\dot {y}}^{2}-2\ell {\dot {y}}{\dot {\theta }}\sin \theta +\ell ^{2}{\dot {\theta }}^{2}.$

上下振動平台上倒單擺的圖，左圖是慢速振動下的響應，右圖是快速振動下的響應

系統的拉格朗日量如下：

$L={\frac {1}{2}}m\left({\dot {y}}^{2}-2\ell {\dot {y}}{\dot {\theta }}\sin \theta +\ell ^{2}{\dot {\theta }}^{2}\right)-mg\left(y+\ell \cos \theta \right)$

運動方程為：

${\mathrm {d} \over \mathrm {d} t}{\partial {L} \over \partial {\dot {\theta }}}-{\partial {L} \over \partial \theta }=0$

結果是：

$\ell {\ddot {\theta }}-{\ddot {y}}\sin \theta =g\sin \theta .$

若y的運動是簡諧運動$y=A\sin \omega t$，則其微分方程為：

${\ddot {\theta }}-{g \over \ell }\sin \theta =-{A \over \ell }\omega ^{2}\sin \omega t\sin \theta .$

此一方程沒有解析解，不過可以用不同方式來求解。若振幅很小時，可以用馬丟函數來近似。分析結果是卡皮察擺在快速振盪時可以穩定。左圖是慢速振盪的圖，在慢速振盪下，單擺很快就倒下，其角度$\theta$很快就超過90°，表示單擺已倒下。右圖是快速振盪的圖，若$y$是快速振盪，擺可以穩定在直立狀態下。啟始時倒單擺是在直立狀態（$\theta =0$），但擺的角度始終不大，而且擺有倒下。

倒單擺的種類

平衡倒單擺是研究者常見的工程挑戰，有許多不同的變形，從台車上的倒單擺到台車上的多段倒擺（倒複擺）。另外一種變體是將倒單擺或是倒複擺放在旋轉元件的末端。若沒有外力平衡，這些倒擺都會倒下。計劃中的倒單擺可能是在找到平衡位置後要可以維持平衡，或是要可以自行達到平衡狀態。另外一個平台是兩輪平衡的倒單擺。兩輪的倒單擺可以旋轉，可以提供相當的操控性。另外一個變體是在單點上的平衡。陀螺、單輪腳踏車或是球上的倒單擺都是單點上平衡的例子。如上所述，若在垂直振盪的平面上，倒單擺也可以維持平衡。

倒單擺的例子

人就是平衡倒單擺的例子之一。站著的人就是倒單擺，其腳即為樞紐，若站著的人沒有肌肉持續的微幅施力調整，最後會跌倒。人的神經系統中有無意識的反饋控制系統、平衡感或正位反射，用眼睛、肌肉及關節的本體感覺，以及由內耳中三個半規管組成前庭系統所得的方向輸入、或是利用耳石的輸入，持續的對骨骼肌小幅調整施力，以維持直立。走路、跑步或是單腳站立都需要此系統的調節。有些疾病、酒精或是藥物中毒會影響此一反射，造成頭暈或無法自行站立平衡。警察在測試駕駛者是否有受到酒精或是藥物影響的現場清醒測試就是確認此反射是否有問題。

像用手平衡直立在手上的掃把或是直尺，也是倒單擺的例子。

有許多的設備中有用到倒單擺，倒單擺的平衡也是研究者探討的工程問題之一。倒單擺本身不穩定的特性，略有一些擾動，就會有明顯的響應，因此也是早期地震儀中的關鍵元件之一。

很多現代的個人運輸工具中也有用到倒單擺的概念，例如二輪的自平衡滑行車以及單輪的電子單輪車。這些設備有動力學不穩定的特性，需要透過電子回授配合伺服機構使其直立。

讓台車上的單擺由單擺往下的穩定狀態，擺動到倒單擺的狀態，是最佳控制的典型玩具問題之一

台車單擺系統，由單擺往下的穩定狀態，擺動到倒單擺的狀態，力平方值最小化的軌跡

相關條目

• 倒雙擺
• 慣性輪單擺
• Furuta擺
• iBOT
• 類人型機器人
• Ballbot

參考資料

• D. Liberzon Switching in Systems and Control (2003 Springer) pp. 89ff

延伸閱讀

• Franklin; et al. (2005). Feedback control of dynamic systems, 5, Prentice Hall. ISBN 0-13-149930-0

外部連結

• YouTube - Inverted Pendulum - Demo #3 （頁面存檔備份，存於網際網路檔案館）
• YouTube - inverted pendulum （頁面存檔備份，存於網際網路檔案館）
• YouTube - Double Pendulum on a Cart （頁面存檔備份，存於網際網路檔案館）
• YouTube - Triple Pendulum on a Cart （頁面存檔備份，存於網際網路檔案館）
• A dynamical simulation of an inverse pendulum on an oscillatory base （頁面存檔備份，存於網際網路檔案館）
• Inverted Pendulum: Analysis, Design, and Implementation
• Non-Linear Swing-Up and Stabilizing Control of an Inverted Pendulum System （頁面存檔備份，存於網際網路檔案館）
• Stabilization fuzzy control of inverted pendulum systems
• Blog post on inverted pendulum, with Python code （頁面存檔備份，存於網際網路檔案館）
• Equations of Motion for the Cart and Pole Control Task （頁面存檔備份，存於網際網路檔案館）