降壓-升壓變換器

（反向型）降壓-升壓變換器的基本架構

降壓-升壓變換器（buck–boost converter），是一種直流-直流轉換器，其輸出電壓大小可以大於輸入電壓，也可以小於輸入電壓。降壓-升壓變換器和返馳式變換器等效，但用單一的電感器來取代變壓器。

有二種不同架構的電路都可以稱為降壓-升壓變換器，兩者輸出電壓的範圍都很大，從（絕對值）較輸出電壓大很多的電壓，到幾乎接近零的電壓。

反向架構

其輸出電壓的極性和輸入電壓相反，這是一種電路類似降壓變換器或是升壓變換器的開關電源。輸出電壓可以由切換功率晶體的占空比調整。

結合降壓變換器及升壓變換器的架構

輸出電壓的電氣極性和輸入電壓相同，可以比輸入電壓小，也可以比輸入電壓大。這類的非反向式轉換器可以在降壓變換器段及升壓變換器共用一個電感器、用開關代替二極體。有時也稱為四個開關的降壓-升壓變換器（four-switch buck-boost converter）。也可以用多個電感器，但像SEPIC變換器或是Ćuk轉換器一樣只用一個開關。

四個開關架構的基本電路

四個開關非反向架構的工作原理

四個開關的變換器結合了升壓變換器以及降壓變換器，並且將升壓變換器和降壓變換器的二個二極體都用功率晶體配合同步整流代替，可以因為功率晶體的低電壓降讓效率再進一步提昇。

四個開關的變換器可以運作在升壓模式或是降壓模式。在任一模式中，都只用一個開關控制占空比，另一個只作續流用，其動作恰好和第一個開關相反，另外二個開關則是在固定的位置。

二個開關反向架構的工作原理

圖2：二個降壓-升壓變換器的圖，當開關導通時，輸入電壓源提供電流至電感器，電容提供電流到電阻（輸出負載）。當開關開路時，電感器藉由二極體D提供電源到負載

降壓-升壓變換器的基本原理如下（參考圖2）：

• 在導通（On）狀態下，輸入電壓源直接接到電感器（L），因此電感器L會開始儲能，因此由電容器提供能量給輸出端的負載。
• 在開路（Off）狀態下，電感器連結到輸出端的負載及電容器，因此能量從電感器L及電容器C提供給負載R。

相較於降壓變換器及升壓變換器，降壓-升壓變換器有以下的特性：

• 輸出電壓的極性和輸入電壓相反。

理想電壓

若假設是理想的轉換器，並假設輸入電壓為正，輸出電壓可以從0到$\scriptstyle -\infty$。降壓變換器及升壓變換器的輸出電壓範圍則分別是$\scriptstyle V_{i}$到0及$\scriptstyle V_{i}$到$\scriptstyle \infty$。

概念簡介

降壓-升壓變換器在原理上類似降壓變換器及升壓變換器，都是利用電感器會避免電流快速變化的特性。一開始時沒有任何元件有帶電，開關開路，流經電感器的電流為0。當開關初次關閉時，二極體讓電流無法從電源流到右側的負載，因此電流都會經過電感器，不過因為通過電感器會避免電流快速變化，因此一開始通過電感器的電流會比較小，之後才緩緩的上昇，此時，電感器也以磁場的方式儲存能量。

連續模式

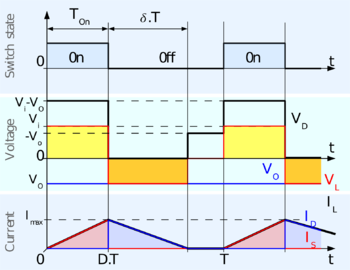
圖3：降壓-升壓變換器在連續模式運行下的電壓及電流波形

若在整個週期中，流經電感器L的電流都不會降到0，此時會稱變換器運作在連續模式，圖3是理想變換器運作在連續模式的電壓及電流。

從$t=0$到$t=T$的時間，轉換器在導通（On）狀態，因此開關S閉合，電感器電流I_L的變化率為

${\frac {\operatorname {d} I_{L}}{\operatorname {d} t}}={\frac {V_{i}}{L}}$

在導通階段最後，I_L的總增加量為：

$\Delta I_{{\text{L}}_{\text{On}}}=\int _{0}^{D\,T}\operatorname {d} I_{\text{L}}=\int _{0}^{D\,T}{\frac {V_{i}}{L}}\,\operatorname {d} t={\frac {V_{i}\,D\,T}{L}}$

D為占空比，是切換週期中T，開關閉合的時間。因此D會在0（S持續開路）及1 （S持續閉合）之間變化。

若在斷路（Off）狀態，開關S會開路，因此電感器電流會流到負載端，假設二極體的壓降為0，且電容器夠大，因此電容器電壓可假設為定值，I_L的變化為：

${\frac {\operatorname {d} I_{\text{L}}}{\operatorname {d} t}}={\frac {V_{o}}{L}}$

因此在斷路狀態下，I_L的總變化量為：

$\Delta I_{{\text{L}}_{\text{Off}}}=\int _{0}^{\left(1-D\right)T}\operatorname {d} I_{\text{L}}=\int _{0}^{\left(1-D\right)T}{\frac {V_{o}\,\operatorname {d} t}{L}}={\frac {V_{o}\left(1-D\right)T}{L}}$

由於假設變換器是在穩態下運作，因此在切換週期開始時，所有元件的儲能都應該和切換週期結束時相同。而電感器的能量為：

$E={\frac {1}{2}}L\,I_{\text{L}}^{2}$

因此可以推得在斷路狀態最後的電流I_L會和導通狀態一開始的電流I_L相等，也就是導通階段的電流變化量加上斷路階段的電流變化量會等於0：

$\Delta I_{{\text{L}}_{\text{On}}}+\Delta I_{{\text{L}}_{\text{Off}}}=0$

替換$\Delta I_{{\text{L}}_{\text{On}}}$及$\Delta I_{{\text{L}}_{\text{Off}}}$可得：

$\Delta I_{{\text{L}}_{\text{On}}}+\Delta I_{{\text{L}}_{\text{Off}}}={\frac {V_{i}\,D\,T}{L}}+{\frac {V_{o}\left(1-D\right)T}{L}}=0$

也可以寫作：

${\frac {V_{o}}{V_{i}}}={\frac {-D}{1-D}}$

因此可以得到：

$D={\frac {V_{o}}{V_{o}-V_{i}}}$

由上述的計算可以看到輸出電壓的極性恆為負的（因為占空比會在0到1之間變化），其絕對值會隨著D增加而增加，若D接近1，輸出電壓理論上會趨近負無限大。降壓-升壓變換器可以作升壓用，也可以做降壓用，因此稱為降壓-升壓變換器

不連續模式

圖4：不連續模式下的電壓和電流

有時負載需要的能量較少，所需要的轉換時間比切換週期要短。因此在整個切換週期中，可能有些時間的電感電流為零。唯一的差異就是在切換週期的最後，有一段時間電感器已經完全放電（參考圖4）。差異看似不大，但是對輸出電壓方程有大的影響。可以計算如下：

因為在切換週期開始時，電感器電流為0，因此$I_{L_{\text{max}}}$在( $t=D\,T$)的最大值為

$I_{L_{\text{max}}}={\frac {V_{i}\,D\,T}{L}}$

在斷路狀態時，I_L會在δ.T後降到0:

$I_{L_{\text{max}}}+{\frac {V_{o}\,\delta \,T}{L}}=0$

使用上述二個方程，可以得到δ為：

$\delta =-{\frac {V_{i}\,D}{V_{o}}}$

負載電流等於平均的二極體電流$I_{D}$。從圖4可以看到，在斷路狀態時，二極體電流等於電感器電流，因此輸出電流可以寫成：

$I_{o}={\bar {I_{D}}}={\frac {I_{L_{\text{max}}}}{2}}\delta$

替換$I_{L_{\text{max}}}$和δ可得：

$I_{o}=-{\frac {V_{i}\,D\,T}{2L}}{\frac {V_{i}\,D}{V_{o}}}=-{\frac {V_{i}^{2}\,D^{2}\,T}{2L\,V_{o}}}$

因此輸出電壓增益是：

${\frac {V_{o}}{V_{i}}}=-{\frac {V_{i}\,D^{2}\,T}{2L\,I_{o}}}$

將上述和連續模式下的輸出電壓增益相比較，這個式子複雜多了。在不連續模式下，輸出電壓增益不只和占空比有關，也和電感器感值、輸入電壓、輸出電流有關。

連續模式及不連續模式的邊界

圖5：Fig 5: 降壓-升壓變換器正規化輸出電壓及正規化輸出電流之間的關係

降壓-升壓變換器的負載電流若比較小，變換器會運作在不連續模式下，若是負載電流比較大，才會運作在連續模式下。兩個模式中間的臨界點出現在電感電流在切換週期最後才變為0的情形下，配合圖4的標示，會對應以下的式子：

$D\,T+\delta \,T=T$

$D+\delta =1\,$

此時，輸出電流$\scriptstyle I_{o_{\text{lim}}}$（臨界狀態下的輸出電流）為：

$I_{o_{\text{lim}}}={\bar {I_{D}}}={\frac {I_{L_{\text{max}}}}{2}}\left(1-D\right)$

將$\scriptstyle I_{L_{\text{max}}}$替換為在不連續模式下的式子，可得：

$I_{o_{\text{lim}}}={\frac {V_{i}\,D\,T}{2L}}\left(1-D\right)$

因為$\scriptstyle I_{o_{\text{lim}}}$是在連續模式及不連續模式邊界時的電流，因此會同時符合連續模式及不連續模式的式子，代入在連續模式下的式子，可得：

$I_{o_{\text{lim}}}={\frac {V_{i}\,D\,T}{2L}}{\frac {V_{i}}{V_{o}}}\left(-D\right)$

然後再導入以下二種導入方式：

• 正規化電壓，定義為$\scriptstyle \left|V_{o}\right|={\frac {V_{o}}{V_{i}}}$。對應變換器的電壓增益。
• 正規化電流，定義為$\scriptstyle \left|I_{o}\right|={\frac {L}{T\,V_{i}}}I_{o}$。 而$\scriptstyle {\frac {T\,V_{i}}{L}}$等於在切換週期下的最大電感電流增加量，也就是當D=1時的電感電流增加量。因此，在變換器穩態運作時，意味著沒有輸出電流時，$\scriptstyle \left|I_{o}\right|$=0，此數值為1時表示變換器已經提供其最大可變換的電流。

配合上述表示方式，可得：

• 連續模式下，$\scriptstyle \left|V_{o}\right|=-{\frac {D}{1-D}}$
• 不連續模式下，$\scriptstyle \left|V_{o}\right|=-{\frac {D^{2}}{2\left|I_{o}\right|}}$;
• 連續模式及不連續模式邊界時的電流為$\scriptstyle I_{o_{\text{lim}}}={\frac {V_{i}\,T}{2L}}D\left(1-D\right)={\frac {I_{o_{\text{lim}}}}{2\left|I_{o}\right|}}D\left(1-D\right)$。因此連續模式及不連續模式邊界的軌跡為$\scriptstyle {\frac {1}{2\left|I_{o}\right|}}D\left(1-D\right)=1$。

上述的結論畫在圖5中，可以看出導通模式及不導通模式下的差異。

非理想元件的影響

雜散電阻的影響

圖6：降壓-升壓變換器在雜散電阻增加時，其占空比和電壓之間的變化

上述的分析中均未考慮變換器中有耗散能量的元件（電阻器），意思是變換器會將電源端的功率完全轉換到負載端，不會有能量損耗。不過電子元件中都會存在寄生元件，例如因為導體材料而產生的寄生電阻。因此變換器需考慮因為寄生電阻而損耗的能量。

為了簡單起見，以下假設只有電感器含有寄生電阻，是唯一的非理想元件，可以等效為電感器上串聯一個電阻。電感器是由長的導體所構成，因此上面的確可能有一個不可忽略的寄生電阻（R_L），而且不論是導通狀態或是斷路狀態，電感器上都有電流流過。

利用狀態空間平均法，可得：

$V_{i}={\bar {V}}_{\text{L}}+{\bar {V}}_{S}$

其中$\scriptstyle {\bar {V}}_{\text{L}}$及$\scriptstyle {\bar {V}}_{S}$ 是切換週期中，電感兩端及開關兩端的平均電壓。若假設變換器是在穩態下運作，電感器的平均電流為定值，則電感器的其平均電壓為：

${\bar {V}}_{\text{L}}=L{\frac {\bar {dI_{\text{L}}}}{dt}}+R_{\text{L}}{\bar {I}}_{\text{L}}=R_{\text{L}}{\bar {I}}_{\text{L}}$

當開關是在導通狀態，$\scriptstyle V_{S}=0$。若開關是在斷路狀態，二極體是在穩向偏壓（假設是工作在連續模式下）。因此$\scriptstyle V_{S}=V_{i}-V_{o}$，則開關二端的平均電壓為：

${\bar {V}}_{S}=D\,0+(1-D)(V_{i}-V_{o})=(1-D)(V_{i}-V_{o})$

在斷路時，輸出電流是電感電流，但符號相反。因此平均電流為：

${\bar {I}}_{\text{L}}={\frac {-I_{o}}{1-D}}$

假設輸出電流及漣波電壓都很小，轉換器的負載可以假設為阻值為R純電阻，上式會變為：

${\bar {I}}_{\text{L}}={\frac {-V_{o}}{(1-D)R}}$

利用上述式子，輸入電壓為：

$V_{i}=R_{\text{L}}{\frac {-V_{o}}{(1-D)R}}+(1-D)(V_{i}-V_{o})$

可以寫成：

${\frac {V_{o}}{V_{i}}}={\frac {-D}{{\frac {R_{\text{L}}}{R(1-D)}}+1-D}}$

若電感器的電阻值為0，上式就會變成理想下的輸出電壓及輸入電壓關係。不過當R_L增加，輸換器的電壓增益會下降。而且當占空比越大，R_L的影響也越大，圖6就是說明上述的影響。

相關條目

• Ćuk 轉換器
• SEPIC變換器

延伸閱讀

• 丹尼爾·W·哈特，《電力電子學導論》，馬鞍河上游普倫蒂斯大廳，美國新澤西州，1997。 ISBN 0-02-351182-6
• 《開關模式電源：SPICE模擬與實用設計》，麥格勞-希爾。ISBN 0-07-150858-9.