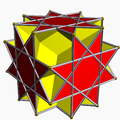
反平行四邊形二十四面體
外觀
 | ||
| 類別 | 均勻多面體對偶 星形多面體 | |
|---|---|---|
| 對偶多面體 | 大斜方立方體 | |
| 識別 | ||
| 名稱 | 反平行四邊形二十四面體 | |
| 參考索引 | DU21 | |
| 數學表示法 | ||
| 威佐夫符號 | 4/3 3/2 2 |[1] | |
| 性質 | ||
| 面 | 24 | |
| 邊 | 48 | |
| 頂點 | 18 | |
| 歐拉特徵數 | F=24, E=48, V=18 (χ=-6) | |
| 組成與佈局 | ||
| 面的種類 | 24個反平行四邊形 | |
| 頂點佈局 | 兩種頂點 4個反平行四邊形的公共頂點 8個反平行四邊形的公共頂點 (星形排佈) | |
| 對稱性 | ||
| 對稱群 | Oh, [4,3], *432 | |
| 特性 | ||
| 等面、非凸 | ||
| 圖像 | ||
| ||
在幾何學中,反平行四邊形二十四面體是一種星形二十四面體,由24個的反平行四邊形組成,其索引編號為DU21[2]。反平行四邊形二十四面體的對偶多面體為大斜方立方體[3]。反平行四邊形二十四面體為數學家溫尼爾的著作《多面體模型》中之形狀W103[4]的對偶多面體[5]。
性質
[編輯]反平行四邊形二十四面體,由24個全等的反平行四邊形組成,其具有48條稜和18個頂點。在其18個頂點中,有12個是4個反平行四邊形的公共頂點、另外6個是8個反平行四邊形的公共頂點[6],然而這6個頂角並非一般的八面角,其對應的頂點圖為八角星,表示其排列方式同於八角星的稜之排佈。
面的組成
[編輯]反平行四邊形二十四面體由24個全等的反平行四邊形(亦稱為領結形)所組成[7]:

|
 反平行四邊形在立體中的位置 |
反平行四邊形具有兩對邊等長的特性[8],因此組成反平行四邊形二十四面體的反平行四邊形有兩種長度的邊。若反平行四邊形二十四面體對應的對偶多面體大斜方立方體其邊長為單位長,則對應的反平行四邊形二十四面體中反平行四邊形面上較短的邊長為[7]:
- 單位長
此時,較長的邊長為[7]:
- 單位長
而其邊長比為。
相關多面體與鑲嵌
[編輯]反平行四邊形二十四面體和星形四角化菱形十二面體皆可以視為將菱形十二面體每個面替換成一個頂點和四個三角形的結果[9],換句話說即將菱形十二面體每個面替換成一個菱形錐,根據替換的角錐錐高的不同,可以產生不同的立體:

|

|

|

|
| 菱形十二面體 | 四角化菱形十二面體 | 星形四角化菱形十二面體 | 反平行四邊形二十四面體 |
大六角二十四面體與反平行四邊形二十四面體幾何中心重合可以組成一個大鳶形二十四面體[10]。
 大六角二十四面體 |
 反平行四邊形二十四面體 |
 大鳶形二十四面體 |
反平行四邊形二十四面體由反平行四邊形(亦稱為領結形)所組成[7],其他同樣由四邊形組成,且具有八面體群對稱性的二十四面體有:
| 圖像 |  鳶形二十四面體 |
 反平行四邊形二十四面體 |
 大鳶形二十四面體 |
 小六角二十四面體 |
 大六角二十四面體 |
 小反平行四邊形二十四面體 |
|---|---|---|---|---|---|---|
| 面 |  鳶形 |
 反平行四邊形 |
 凹鳶形 |
 凹鳶形 露出的部分為 反平行四邊形 |
 鳶形 |
 反平行四邊形 |
參見
[編輯]參考文獻
[編輯]- ^ Dual 21: great rhombihexacron. gratrix.net. [2019-09-07]. (原始內容存檔於2008-12-04).
- ^ Wenninger, Magnus, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 0730208
- ^ Eric W. Weisstein. Great Rhombihexacron. 密歇根州立大學圖書館. [2019-09-07]. (原始內容存檔於2014-07-11).
- ^ Wenninger, Magnus. Polyhedron Models. Cambridge University Press. 1974. ISBN 0-521-09859-9.
- ^ Weisstein, Eric W. (編). Great Rhombihexacron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英語).
- ^ Great Rhombihexacron. kitwallace.co.uk. [2019-09-07]. (原始內容存檔於2021-09-03).
- ^ 7.0 7.1 7.2 7.3 David I. McCooey. Versi-Quasi-Regular Duals: Great Rhombihexacron. dmccooey.com. [2019-09-07]. (原始內容存檔於2018-03-10).
- ^ Bryant, John; Sangwin, Christopher J., 3.3 The Crossed Parallelogram, How round is your circle? Where Engineering and Mathematics Meet, Princeton University Press: 54–56, 2008, ISBN 978-0-691-13118-4.
- ^ Hexakis Octahedron. Florida Center for Instructional Technology, College of Education, University of South Florida. [2019-09-03]. (原始內容存檔於2015-01-21).
- ^ Great Hexacronic Icositetrahedron. software3d.com. [2019-09-07]. (原始內容存檔於2015-11-21).