内射模(英语:injective module),在模论中,是具有与有理数  (视为
(视为  -模)相似性质的模。内射模是投射模的对偶概念,由Reinhold Baer于1940年引进。
-模)相似性质的模。内射模是投射模的对偶概念,由Reinhold Baer于1940年引进。
一个环  上的左模
上的左模  若满足以下等价条件,则称之为内射模:
若满足以下等价条件,则称之为内射模:
- 若
 是另一个左
是另一个左  -模
-模  的子模,则存在另一个子模
的子模,则存在另一个子模  使得
使得  。
。
- 若
 是左
是左  -模的单射,
-模的单射, 为同态,则存在同态
为同态,则存在同态  使得
使得  。图示如下:
。图示如下:
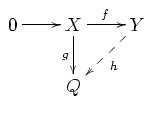
- 任何短正合序列
 都分裂。
都分裂。
- 函子
 为正合函子。
为正合函子。
右模的定义类此。抽象地说,内射模乃是模范畴中的内射对象。
- 零模是内射模的平凡例子。
- 设
 为域,则任何
为域,则任何  -模(即
-模(即  -向量空间)都是内射模,此点可由基的性质证明。
-向量空间)都是内射模,此点可由基的性质证明。
- 设
 为紧群(例如有限群),
为紧群(例如有限群), 为特征为零的域。根据紧群的表示理论,可知任何表示的子表示都是其直和项;若翻译为模的语言,即是:群代数
为特征为零的域。根据紧群的表示理论,可知任何表示的子表示都是其直和项;若翻译为模的语言,即是:群代数  上的所有模都是内射模。
上的所有模都是内射模。
- 设
 为域
为域  上含单位元的有限维结合代数。则逆变函子
上含单位元的有限维结合代数。则逆变函子  给出有限生成左
给出有限生成左  -模与有限生成右
-模与有限生成右  -模的对偶性。因此,有限生成的左
-模的对偶性。因此,有限生成的左  -模在同构的意义下皆可写作
-模在同构的意义下皆可写作  ,其中
,其中  是某个有限生成的投射右
是某个有限生成的投射右  -模。
-模。
- 在一般的环上也存在充足的(在内射分解的意义下)投射模,以下将述及相关理论。初步的例子包括:
 对加法形成内射
对加法形成内射  -模。群
-模。群  (
( )是内射
)是内射  -模,而非内射
-模,而非内射  -模。
-模。
- 若一个环作为它自身的左模是内射的,就称为一个左自内射环(英语:left self-injective ring)。右自内射环可对称的定义。半单环,整数的剩余类环是自内射环。一个左自内射环不一定是右自内射的。
内射模的直积(包括无穷直积)仍是内射模,内射模的有限直和仍为内射模。一般而言,内射模的子模、商模或无穷直和并不一定是内射模。
Baer 在其论文中证明了一个有用的结果,通常称作 Baer 判准:一个左  -模
-模  是内射模当且仅当定义在任一理想
是内射模当且仅当定义在任一理想  上的态射
上的态射  都能延拓到整个
都能延拓到整个  上。
上。
利用此判准,可证明主理想域  上的模
上的模  是内射模当且仅当
是内射模当且仅当  可除,即:对任何
可除,即:对任何  ,存在
,存在  使得
使得  ,由此可证
,由此可证  是内射
是内射  -模,向量空间都是内射模。
-模,向量空间都是内射模。
最重要的内射模当属  :它是
:它是  -模范畴中的内射上生成元,换言之,这是内射模,而且任何
-模范畴中的内射上生成元,换言之,这是内射模,而且任何  -模皆可嵌入某个
-模皆可嵌入某个  中,其中
中,其中  是够大的基数。由此可知任何
是够大的基数。由此可知任何  -模皆可嵌入某个内射
-模皆可嵌入某个内射  -模。此性质对任意环
-模。此性质对任意环  上的左模都成立,要点在于利用
上的左模都成立,要点在于利用  的特性构造左
的特性构造左  -模范畴中的内射上生成元。
-模范畴中的内射上生成元。
我们也可以定义模的内射包(基本上是包含一个模的最小内射模)。任意模  都有内射分解,这是形式如下的正合序列:
都有内射分解,这是形式如下的正合序列:

其中每个  都是内射的。内射分解可以用以定义模的内射维度(基本上是内射分解的最短长度,可能是无限的)及导函子。
都是内射的。内射分解可以用以定义模的内射维度(基本上是内射分解的最短长度,可能是无限的)及导函子。
不可分解内射模的自同态环是局部环。
- F.W. Anderson and K.R. Fuller: Rings and Categories of Modules, Graduate Texts in Mathematics, Vol. 13, 2nd Ed., Springer-Verlag, New York, 1992.