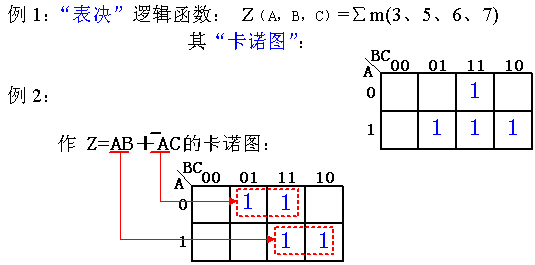
卡诺图
外观
此条目可参照英语维基百科相应条目来扩充。 |
在逻辑代数中,卡诺图(Karnaugh map)是真值表的变形,它可以将有n个变量的逻辑函数的个最小项组织在给定的长方形表格中,同时为相邻最小项(相邻与项)运用邻接律化简提供了直观的图形工具。但是,如果需要处理的逻辑函数的自变量较多(有五个或更多的时候,此时有些项就很难圈了),那么卡诺图的行列数将迅速增加,使图形更加复杂。[1]:189
卡诺图是贝尔实验室的电信工程师莫里斯·卡诺(Maurice Karnaugh)在1953年发明的。
变量卡诺图
[编辑]- 表示各最小项的(n-变量数)个小格,排列呈矩形。
- 小格按“格雷码” 排列,保证最小项间“几何相邻”与“逻辑相邻性”的统一。(几何相邻有“内相邻” “外相邻”和“中心对称”)
函数卡诺图
[编辑]- 最小项():把函数包含的所有最小项,以“1”填入变量卡诺图对应编号的小格内。
- 最大项():把函数包含的所有最大项,以“0”填入变量卡诺图对应编号的小格内。
用卡诺图化简逻辑函数的步骤
[编辑]- 如果表达式为最小项表达式,则可直接填入卡诺图
- 如表达式不是最小项表达式,但是“与—或表达式”,可将其先化成最小项表达式,再填入卡诺图。也可直接填入。
- 合并相邻的最小项,即根据下述原则画圈
- 尽量画大圈,但每个圈内只能含有(n=0,1,2,3……)个相邻项。要特别注意对边相邻性和四角相邻性。
- 圈的个数尽量少。
- 卡诺图中所有取值为1的方格均要被圈过,即不能漏下取值为1的最小项。
- 在新画的包围圈中至少要含有1个未被圈过的1方格,否则该包围圈是多余的。
- 写出化简后的表达式。每一个圈写一个最简与项,规则是,取值为l的变量用原变量表示,取值为0的变量用反变量表示,将这些变量相与。然后将所有与项进行逻辑加,即得最简与—或表达式。
在进行化简时,如果用图中真值为0的项更方便,可以用他们来处理,方法和真值取1时一样,只是结果要再做一次求反。
示例
[编辑]示例--2变量卡诺图
[编辑]-
Σm(0); K = 0
-
Σm(1); K = A′B′
-
Σm(2); K = AB′
-
Σm(3); K = A′B
-
Σm(4); K = AB
-
Σm(1,2); K = B′
-
Σm(1,3); K = A′
-
Σm(1,4); K = A′B′ + AB
-
Σm(2,3); K = AB′ + A′B
-
Σm(2,4); K = A
-
Σm(3,4); K = B
-
Σm(1,2,3); K = A' + B′
-
Σm(1,2,4); K = A + B′
-
Σm(1,3,4); K = A′ + B
-
Σm(2,3,4); K = A + B
-
Σm(1,2,3,4); K = 1
示例--4变量卡诺图
[编辑]一个4变量卡诺图的例子:
| A | B | C | D | ||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 1 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 | 1 |
| 11 | 1 | 0 | 1 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 | 1 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 1 | 1 | 0 |
我们可以用两个不同的写法,及四个不同的布尔变量A, B, C, D和他们的相反值,来表示同一个尚未化简的布尔代数:
- 这个是卡诺图的最小项(即圈出来的值在真值表上显示为1)。
- 这个 是卡诺图的最大项(即圈出来的值在真值表上显示为0)。
| A B C D |
0 0 | 0 1 | 1 1 | 1 0 |
|---|---|---|---|---|
| 0 0 | 0 | 0 | 1 | 1 |
| 0 1 | 0 | 0 | 1 | 1 |
| 1 1 | 0 | 0 | 0 | 1 |
| 1 0 | 0 | 1 | 1 | 1 |
| A B C D |
0 0 | 0 1 | 1 1 | 1 0 |
|---|---|---|---|---|
| 0 0 | 0 | 0 | 1 | 1 |
| 0 1 | 0 | 0 | 1 | 1 |
| 1 1 | 0 | 0 | 0 | 1 |
| 1 0 | 0 | 1 | 1 | 1 |
按照上述卡诺图圈法(不限于上述两种),可知化简结果为AC'+AB'C+BCD'或ABC'+AB'+BCD'
参考文献
[编辑]引注
[编辑]- ^ Stephen Brown, Zvonko Vranesic. Fundamentals of Digital Logic with Verilog Design. McGraw-Hill Education. 2002. ISBN 0-07-283878-7.
来源
[编辑]- 期刊文章
- Karnaugh, Maurice. The Map Method for Synthesis of Combinational Logic Circuits. Transactions of American Institute of Electrical Engineers part I. November 1953, 72 (9): 593–599.