驴桥定理

驴桥定理(拉丁语:Pons asinorum),也称为等腰三角形定理,是在欧几里得几何中的一个数学定理,是指等腰三角形二腰对应的二底角相等。此定理出现在欧几里得的几何原本第一卷命题五。
有关其名称驴桥定理的由来有二种:一种是几何原本中的示意图即为一座桥;另外一种较为大家接受的说法,则是指这是几何原本中第一个对于读者智力的测试,并且做为后续更困难命题的桥梁[1]。几何学是列在中世纪的四术之中,驴桥定理是在几何原本的前面出现的较困难命题,是数学能力的一个门槛,也称之为“笨蛋的难关”[2],无法理解此一命题的人可能也无法处理后面更难的命题。
无论其名称的由来为何,驴桥定理一词已变成了一种隐喻,暗示对能力或了解程度的关键测试,可以区分了解及不了解的人[3]。
证明[编辑]
欧几里得的证明[编辑]

欧几里得的证明包括第二个结论,就是若三角形的二腰延伸超过底边,则二腰延长线和底边的夹角也会相等。欧几里得的证明中包括了绘制二腰延长线的辅助线,但当时的数学家普罗克鲁斯指出他没有用到第二个结论,而且若在三角形内部绘辅助线,会使证明比较简单。欧几里得的证明用到称为SAS的三角形全等,是几何原本中的上一个命题。[4]
其他证明方式[编辑]
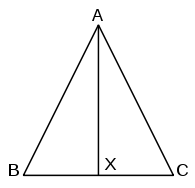
在教科书(例如人教版数学教科书在八年级“轴对称”一章)上常见的作法是作顶角A的角平分线[5]。此证明方式比欧几里德的简单,但在几何原本中命题9才是作角平分线[6],因此若几何原本中在命题5就使用角平分线,会有循环论证的问题。
其证明如下:
- 令三角形为ABC,其中线段AB = 线段AC。
- 作角BAC的角平分线,和线BC交与X点。
- 线段AB = 线段AC,线段AX和自身等长,而且角BAX = 角CAX,因此依照SAS全等,三角形BAX和CAX全等,因此可得角B和角C相等。
勒让德在《几何原理》用了一个类似的方式证明,不过令X是线段BC的中点[7]。其证明方式类似,但是会用到SSS全等,而在欧几里德的几何原本未提到SSS全等。
帕普斯在约公元300年用了一个非常简短的方法证明: 等腰三角形ABC中, AB=AC, BC=CB, CA=BA, 则三角形ABC与ACB全等(SSS), 故三角形ABC 两底角相等 Q.E.D. 在约1960年,赫伯特·吉伦特编写的程序也得到了相同的证明。[8]
用作隐喻的驴桥定理[编辑]
- 十四世纪作家理查德·昂格维尔在《书之爱》中将驴桥定理比拟为没有梯子辅助的陡峭山坡,感叹多少可能成为几何学家的人因此而回头[9]。
- 在直言三段论中,“驴桥”作为寻找三段论中项的一个隐喻,同时有桥梁及考验的含意在内[9]。
- 经济学家约翰·斯图尔特·密尔认为David Ricardo的地租理论是经济学中的驴桥定理[10]。
- 驴桥也是魔术方块中的一个特殊组态。
相关条目[编辑]
参考资料[编辑]
- ^ D.E. Smith History of Mathematics (1958 Dover) p. 284
- ^ 吴任哲. 利用『驢橋定理』探討國中教師之數學教學. HPM通讯第四卷8,9期合刊. [2013-08-21]. (原始内容存档于2013-08-04).
- ^ Pons asinorum - Definition and More from the Free Merriam. [2013-08-21]. (原始内容存档于2010-02-20).
- ^ 第一卷命題五. [2016-07-02]. (原始内容存档于2016-07-10).
- ^ 例如J.M. Wilson Elementary geometry (1878 Oxford) p. 20
- ^ 洪万生. 驢橋定理. 科学月刊1983年4月160期. [2013-08-21].[永久失效链接]
- ^ A. M. Legendre Éléments de géométrie (1876 Libr. de Firmin-Didot et Cie) p. 14
- ^ 侯世达. 哥德尔、艾舍尔、巴赫——集异壁之大成. 商务印书馆. 1996 p. 796
- ^ 9.0 9.1 A. F. West & H. D. Thompson "On Dulcarnon, Elefuga And Pons Asinorum as Fanciful Names For Geometrical Propositions" The Princeton University bulletin Vol. 3 No. 4 (1891) p. 84
- ^ Henry Dunning Macleod The Elements of Economics (1886 D. Appleton) Vol. 2 p. 96
