秒差距

秒差距
秒差距
	1秒差距指的是從太陽至某一天體間，具有1角秒（英語：Minute and second of arc#Symbols and abbreviations）視差的長度（非等比例繪製）
單位信息
單位制	天文單位系統
物理量名稱	長度/距離
符號	pc
單位換算
1 pc	相當於
米制（SI）單位	3.0857×1016 米 ; ~31拍米
英制與美制單位	1.9174×1013 mi
天文單位系統	2.0626×105 au; 3.26156 ly

秒差距（英語：parsec，符號為pc）是一個宇宙距離尺度，用以測量太陽系以外天體距離的單位。1秒差距約為3.26光年、206,000天文單位或 3.085677585519*10¹⁶ 公尺（19兆英里）^[a] 。秒差距的原理使用了視差與三角學，其定義為1天文單位的對角為1角秒時的距離^[1]，但於2015年時被重新定義為一個精確值：7005648000000000000♠648000/ $π$ 天文單位。離太陽最近的恆星比鄰星，距離大約為1.3秒差距（4.2光年）^[2]。絕大多數位於距太陽500秒差距(1630光年)內的恆星，可以在夜空中以肉眼看見。

秒差距最早於1913年，由英國天文學家赫伯特·霍爾·特納提出^[3]。其英語名稱為一個混成詞，由「1角秒（arcsecond）的視差（parallax）」組合而來，使天文學家可以只從原始觀測數據，就能夠進行天文距離的快速計算。由於上述部分原因，即使光年在科普文字與日常使用（英語：Usage）上維持優勢地位，秒差距仍受到天文學與天體物理學的喜愛。秒差距適用於銀河系內的短距離表述，但在描述宇宙大尺度的用途上，會將其加上詞頭來應用，如千秒差距（kpc）表示銀河系內與周圍物體的距離，百萬秒差距（Mpc）描述銀河系附近所有星系的距離，吉秒差距（Gpc）則是描述極為遙遠的星系與眾多類星體。

2015年8月，國際天文學聯合會通過B2決議文，將絕對星等與熱星等（英語：bolometric magnitude）進行標準定義，也包含將秒差距定義為一個精確值，即7005648000000000000♠648000/ $π$ 天文單位，或大約7016308567758149137♠3.08567758149137×10¹⁶公尺（基於2012年國際天文學聯合會對於天文單位的精確國際單位制定義）。此定義對應於眾多當代天文學文獻中對於秒差距的小角度定義^[4]^[5]。

基礎定義

秒差距是一種最古老的，同時也是最標準的測量恆星距離的方法。它是建立在恆星視差的基礎上。

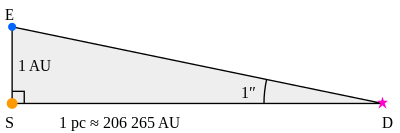
想像待測的恆星與一條地球公轉軌道的半徑線段（即一個天文單位長度）所成的三角形，分別度量待測恆星到太陽及到地球的邊長、與這兩條邊的夾角。當這個夾角為一角秒時，這個三角形是如此的狹長、以至於這兩條邊長可視為相等，那麼這個邊長即稱為一秒差距。此時這個三角形既可視為等腰三角形、又可視為直角三角形（因剩餘的兩個角極其接近直角）。

更詳細地說，周年視差 $\pi =1''$ 的恆星與地球的距離 $r=206\,265\,\mathrm {AU}$ ，這個距離定義為一秒差距（ $1\,\mathrm {pc}$ ）。

計算秒差距的值

在上圖中（非等比例繪製），S代表太陽，E代表地球在軌道上的一個點。因此ES的距離就是1天文單位（au）。假設角SDE為1角秒（1度的1/3600），D為太空當中的某一點，因此依據上述定義，該點與太陽間的距離就稱為1秒差距。根據三角學，SD的距離可由下列方式計算出來：

\mathrm {\tan 1''} ={\frac {\mathrm {ES} }{\mathrm {SD} }}

使用小角度近似^[b]，也就是極端小角度的正切值近乎等同於該角度本身（以弧度表示）：

\mathrm {SD} \approx {\frac {\mathrm {ES} }{1''}}={\frac {1\,{\mbox{AU}}}{{\frac {1}{60\times 60}}\times {\frac {\pi }{180}}}}={\frac {648\,000}{\pi }}\,{\mbox{AU}}\approx 206\,264.81\,{\mbox{AU}}

由於1天文單位被定義為7011149597870700000♠149597870700 米=^[6]，因此可以計算出下列值：

1秒差距	≈ 7005206264806247096♠206264.806247096天文單位
	≈ 7016308567758100000♠3.085677581×10¹⁶公尺
	≈ 7001191735115770000♠19.173511577兆英里
	≈ 7000326156377700000♠3.261563777光年

長度單位

**使用秒差距的長度單位**
長度單位	縮寫	表示	備註
秒差距	pc	3.261光年（近似值）	可用於測量鄰近恆星之間的距離。
千秒差距	kpc	1000秒差距	可用於測量星系或星系團內部天體之間的距離。
百萬秒差距	Mpc	1,000,000秒差距	用於測量鄰近星系或星系團之間的距離。
十億秒差距（吉秒差距）	Gpc	1,000,000,000秒差距	可用於測量大尺度纖維狀結構（比如CfA2長城）的距離和長度或類星體的距離。
兆秒差距（太秒差距）	Tpc	1,000,000,000,000秒差距

天體視差

天體的視差越大，則其距離就越近。反之，則視差越小，離我們越遠。離我們最近的恆星（太陽除外）比鄰星的距離約為1.29pc（4.22光年）。

註腳

^ 這裡的一兆是短尺度，即10¹²（一百萬的百萬，或長尺度上的十億）。
^ 對於此計算方式，其誤差值約為10億分之一（6991100000000000000♠1×10⁻⁹）。

參考文獻

^ Cosmic Distance Scales - The Milky Way. [24 September 2014]. （原始內容存檔於2015-08-10）.
^ Benedict, G. F.; et al. Astrometric Stability and Precision of Fine Guidance Sensor #3: The Parallax and Proper Motion of Proxima Centauri (PDF). Proceedings of the HST Calibration Workshop: 380–384. [11 July 2007]. （原始內容存檔 (PDF)於2016-09-09）.
^ Dyson, F. W. The Distribution in Space of the Stars in Carrington's Circumpolar Catalogue. Monthly Notices of the Royal Astronomical Society. 1913-03-14, 73 (5): 334–342. Bibcode:1913MNRAS..73..334D. ISSN 0035-8711. doi:10.1093/mnras/73.5.334 （英語）. There is a need for a name for this unit of distance. Mr. Charlier has suggested Siriometer ... Professor Turner suggests parsec, which may be taken as an abbreviated form of 'a distance corresponding to a parallax of one second'.
^ Cox, Arthur N.; Pilachowski, Catherine A. Allen's Astrophysical Quantities. Physics Today. 2000-10, 53 (10): 77–78 [2021-09-06]. Bibcode:2000asqu.book.....C. ISSN 0031-9228. doi:10.1063/1.1325201. （原始內容存檔於2022-01-06）（英語）.
^ Binney, James; Tremaine, Scott. Galactic Dynamics 2nd ed. 2008-01-01 [2022-04-17]. Bibcode:2008gady.book.....B. ISBN 978-0-691-13026-2. OCLC 254909523. （原始內容存檔於2022-02-04）.
^ International Astronomical Union (編), RESOLUTION B2 on the re-definition of the astronomical unit of length (PDF), RESOLUTION B2, Beijing: International Astronomical Union, 31 August 2012 [2017-11-01], （原始內容存檔 (PDF)於2013-08-16）, The XXVIII General Assembly of International Astronomical Union recommends [adopted] that the astronomical unit be redefined to be a conventional unit of length equal to exactly 7011149597870700000♠149597870700 米, in agreement with the value adopted in IAU 2009 Resolution B2

[兆-1] 這裡的一兆是短尺度，即10¹²（一百萬的百萬，或長尺度上的十億）。

[7] 對於此計算方式，其誤差值約為10億分之一（6991100000000000000♠1×10⁻⁹）。

[2] Cosmic Distance Scales - The Milky Way. [24 September 2014]. （原始內容存檔於2015-08-10）.

[3] Benedict, G. F.; et al. Astrometric Stability and Precision of Fine Guidance Sensor #3: The Parallax and Proper Motion of Proxima Centauri (PDF). Proceedings of the HST Calibration Workshop: 380–384. [11 July 2007]. （原始內容存檔 (PDF)於2016-09-09）.

[dyson-4] Dyson, F. W. The Distribution in Space of the Stars in Carrington's Circumpolar Catalogue. Monthly Notices of the Royal Astronomical Society. 1913-03-14, 73 (5): 334–342. Bibcode:1913MNRAS..73..334D. ISSN 0035-8711. doi:10.1093/mnras/73.5.334 （英語）. There is a need for a name for this unit of distance. Mr. Charlier has suggested Siriometer ... Professor Turner suggests parsec, which may be taken as an abbreviated form of 'a distance corresponding to a parallax of one second'.

[5] Cox, Arthur N.; Pilachowski, Catherine A. Allen's Astrophysical Quantities. Physics Today. 2000-10, 53 (10): 77–78 [2021-09-06]. Bibcode:2000asqu.book.....C. ISSN 0031-9228. doi:10.1063/1.1325201. （原始內容存檔於2022-01-06）（英語）.

[6] Binney, James; Tremaine, Scott. Galactic Dynamics 2nd ed. 2008-01-01 [2022-04-17]. Bibcode:2008gady.book.....B. ISBN 978-0-691-13026-2. OCLC 254909523. （原始內容存檔於2022-02-04）.

[8] International Astronomical Union (編), RESOLUTION B2 on the re-definition of the astronomical unit of length (PDF), RESOLUTION B2, Beijing: International Astronomical Union, 31 August 2012 [2017-11-01], （原始內容存檔 (PDF)於2013-08-16）, The XXVIII General Assembly of International Astronomical Union recommends [adopted] that the astronomical unit be redefined to be a conventional unit of length equal to exactly 7011149597870700000♠149597870700 米, in agreement with the value adopted in IAU 2009 Resolution B2

[a]

[1]

[2]

[3]

[4]

[5]

[b]

[6]

閱論編長度單位
公制	公尺（m）奎米（Qm）羅米（Rm）佑米（Ym）皆米（Zm）艾米（Em）拍米（Pm）兆米（Tm）吉米（Gm）百萬公尺（Mm）公里（km）公引（hm）公丈（dam）公寸（dm）公分（cm）公釐（mm）絲米（dmm）忽米（cmm）微米（μm）奈米（nm）皮米（微微米）（pm）飛米（費米）（fm）阿米（am）介米（zm）攸米（ym）柔米（rm）虧米（qm）
市制	里引丈尺寸分釐毫
英制／美國慣用單位	英里（哩、咪）（mi）化朗（furlong）鏈（chain）桿（rod）英尋（噚）（fathom）碼（yd）英尺（呎）（ft）英寸（吋）（in）
東亞傳統	堂里引丈仞尺、咫寸分釐（換算另見中國度量衡）
天文學	秒差距（pc）光年（ly）天文單位（AU）月球距離（LD）
台制	尺寸分厘
專屬單位	海里（浬）（NM, Nm, nm, nmi, n mile）鏈 (海事)（cable）埃（Å）點（pt）派卡（pc）條
自然單位	普朗克長度

閱論編天文學長度單位
地球半徑（R_🜨或R_E）光秒（ls）太陽半徑（R_☉）京米（Gm）天文單位（AU）光年（ly）秒差距（pc）
參見：宇宙距離尺度 · 數量級 · 單位換算