分子振動
分子振動是指分子內原子間進行的週期性來回運動,而不包含分子的移動和轉動。這種週期性的運動頻率稱為振動頻率。在光譜學上常用紅外吸收光譜法與拉曼光譜學來測量分子的振動頻率,並用來分析分子結構。
振動座標系[编辑]
一個擁有 n 個原子的非線性分子有 3n − 6 個振動正交模(vibrational normal mode),其餘為 3 個轉動、3 個移動。而線性的分子有 3n − 5 個振動正交模,只有 2 個轉動[1]。雙原子分子為線性分子,所以有一個振動模。每一振動正交模有其不同的振動頻率。分子的振動正交模可透過群論的點群來分析[2]。
範例[编辑]
以乙烯 (C2H4) 作為例子,C2H4 有 6 × 3 − 6 = 12 個振動模:

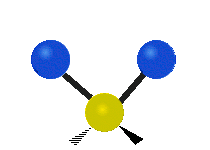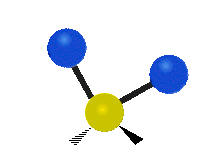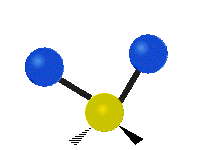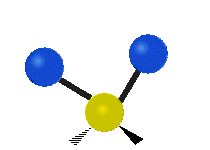
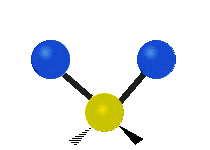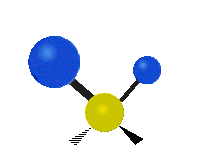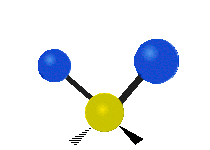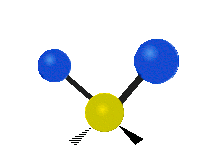
其中,有 4 個 C-H 伸展 (stretching)、1 個 C=C 伸展、2 個 H-C-H 剪式運動 (scissoring)、1 個 H-C-H 擺動 (rocking)、1 個 C-C-H 擺動、2 個 H-C-H 搖擺 (wagging)與1 個 H-C-H 扭轉 (twisting)。在擺動、搖擺與扭轉模,原子間的鍵長不會改變。
| 對稱伸展 | 不對稱伸展 | 平面剪式運動 |
|---|---|---|
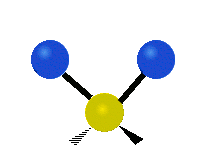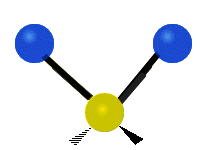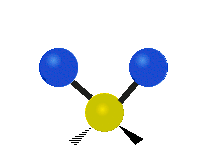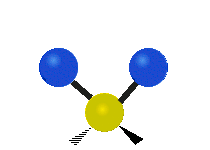
|
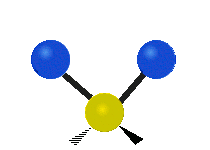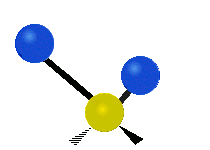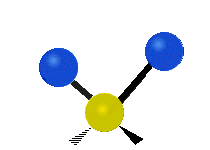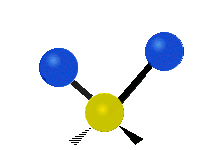
|

|
| 平面擺動 | 非平面搖擺 | 非平面扭轉 |
|

|
|
乙烯的對稱性屬於 D2h 點群,下表列出其 12 個振動正交模及其對應點群的不可約表示 (irreducible representation )、頻率及紅外(Infrared active,IR active)與拉曼活性(Raman active):
| 振動正交模 | 不可約表示 | 頻率 | 紅外活性 | 拉曼活性 |
|---|---|---|---|---|
| C-H 對稱伸展 | b1u | 3217 cm-1 | 是 | 否 |
| C-H 對稱伸展 | ag | 3210 cm-1 | 否 | 是 |
| C-H 不對稱伸展 | b2u | 3185 cm-1 | 是 | 否 |
| C-H 不對稱伸展 | b3g | 3153 cm-1 | 否 | 是 |
| C-C 對稱伸展 | ag | 1827 cm-1 | 否 | 是 |
| H-C-H 平面剪式運動 | b1u | 1413 cm-1 | 是 | 否 |
| H-C-H 平面剪式運動 | ag | 1388 cm-1 | 否 | 是 |
| C-C-H 平面擺動 | b3g | 1167 cm-1 | 否 | 是 |
| H-C-H 非平面搖擺 | b3u | 1068 cm-1 | 是 | 否 |
| H-C-H 非平面搖擺 | b2g | 1057 cm-1 | 否 | 是 |
| H-C-H 非平面扭轉 | au | 875 cm-1 | 否 | 否 |
| H-C-H 平面擺動 | b2u | 835 cm-1 | 是 | 否 |
量子化學[编辑]
在處理正交振動模時,量子化學使用簡諧運動來近似處理分子振動。解薛丁格方程式可獲得以下的振動能階公式:
其中 n 為振動量子數 0, 1, 2,...,可用來代表其振動能階、振動量子態,詳細推導請參閱量子諧振子。
參閱[编辑]
參考文獻[编辑]
- ^ Landau LD and Lifshitz EM (1976) Mechanics, 3rd. ed., Pergamon Press. ISBN 0-08-021022-8 (hardcover) and ISBN 0-08-029141-4 (softcover)
- ^ Cotton, F. A., Chemical Applications of Group Theory, John Wiley & Sons: New York, 1990. ISBN 0471510947
| ||||||||||||||||||||||||||||||||

