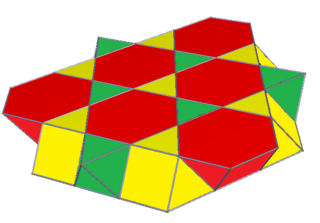
截半立方體堆砌
外观
| 截半立方體堆砌 | |
|---|---|
 | |
 線架圖 | |
| 類型 | 均勻堆砌 |
| 維度 | 3 |
| 對偶多胞形 | 雙四角錐堆砌 |
| 類比 | 截半正方形鑲嵌 |
| 數學表示法 | |
| 考克斯特符號 | |
| 纖維流形記號 | 4−:2 |
| 施萊夫利符號 | r{4,3,4} or t1{4,3,4} r{3[4]} |
| 性質 | |
| 胞 | r{4,3} {3,4} |
| 面 | {3} {4} |
| 組成與佈局 | |
| 顶点图 |  長方體 |
| 對稱性 | |
| 對稱群 | |
| 空間群 | Pm3m (221) |
| 考克斯特群 | , [4,3,4] |
| 特性 | |
| 顶点正 | |
在幾何學中,截半立方體堆砌是一種歐幾里得三維空間的半正堆砌,由截半立方體和正八面體堆砌而成,是三維空間內28個半正密鋪之一,其對偶多面體為雙四角錐堆砌。
康威稱截半立方體堆砌為cuboctahedrille[1],因為它可以藉由立方體堆砌經過「截半」變換構造而來,也可以視為由截半立方體堆砌而得,但截半立方體無法單獨堆砌,必須和其他多面體一起堆砌,而截半立方體堆砌是由截半立方體和正八面體共同堆砌而得。
表面塗色[编辑]
| 對稱性 | [4,3,4] |
[1+,4,3,4] [4,31,1], |
[4,3,4,1+] [4,31,1], |
[1+,4,3,4,1+] [3[4]], |
|---|---|---|---|---|
| 空間群 | Pm3m (221) |
Fm3m (225) |
Fm3m (225) |
F43m (216) |
| 表面塗色 | 
|
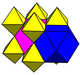
|

|

|
| 考克斯特符號 | ||||
| 頂點圖 | 
|
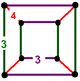
|

|

|
| 頂點 值 對稱性 |
D4h [4,2] (*224) order 16 |
D2h [2,2] (*222) order 8 |
C4v [4] (*44) order 8 |
C2v [2] (*22) order 4 |
結構[编辑]
截半立方體堆砌可以被切割出一個截半六邊形鑲嵌的面,從截半立方體的六邊形中心切割,創建了兩個正三角帳塔。這部分的結構均勻,可用考克斯特記號![]()
![]()
![]()
![]()
![]()
![]()
![]() 表示,符號為s3{2,6,3}。
表示,符號為s3{2,6,3}。
参考文獻[编辑]
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (包含11个凸半正镶嵌、28个凸半正堆砌、和143个凸半正四维砌的全表)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication参与编辑, 1995, ISBN 978-0-471-01003-6 [1]
- (22页) H.S.M.考克斯特, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 半正空间镶嵌)
- A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)