法布里-珀罗干涉仪
在光学中,法布里-佩罗干涉仪(英文:Fabry–Pérot interferometer)是一种由两块平行的玻璃板组成的多光束干涉仪,其中两块玻璃板相对的内表面都具有高反射率。法布里-佩罗干涉仪也经常称作法布里-佩罗谐振腔、F-P腔或法-珀腔(英語:F-P Cavity),并且当两块玻璃板间用固定长度的空心间隔物来间隔固定时,它也被称作法布里-佩罗标准具或直接简称为标准具(来自法语étalon, 意为“测量规范”或“标准”[1]),但这些术语在使用时并不严格区分。这一干涉仪的特性为,当入射光的频率满足其共振条件时,其透射频谱会出现很高的峰值,对应着很高的透射率。法布里-佩罗干涉仪这一名称来自法国物理学家夏尔·法布里和阿尔弗雷德·佩罗[2]。
法布里-佩罗干涉仪的共振特性和二项色性滤镜所利用的共振特性是相同的。实质上,二项色性滤镜是由很薄的法布里-佩罗干涉仪组连续排列得到的,从而在设计上它们有着相同的数学处理方法。法布里-佩罗干涉仪还被广泛应用在通信、激光和光谱学领域,它主要用於精确测量和控制光的频率和波长。当代工艺已经能够制造出非常精密且可调谐的法布里-佩罗干涉仪。
理论解释[编辑]

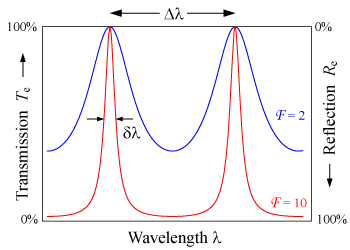
对於法布里-珀罗标准具而言,其透射率随波长的显著变化是由于两块反射板之间多重反射光的干涉。当透射光为同相时它们有相长干涉,对应着标准具透射率的峰值;而当透射光反相时则对应着透射率的极小值。多重反射光彼此是否同相,取决于入射光的频率、光线在标准具内传播的折射角、标准具的厚度及其所用材料的折射率。
法布里-珀罗标准具中,两束相邻的反射光之间的光程差,在不考虑相移时的相位差为[3]
另外,内界面反射率都为,则标准具的透射率函数由下式给出
其中。
当相邻两束光之间的光程差为波长的整数倍时,透射率函数有最大值1。在介质无吸光的情形下,标准具的反射率满足
当,也就是光程差为波长的半奇数倍时透射率函数有最小值,此时对应着反射率的最大值
在透射率函数上,两个相邻的透射峰值之间的波长间隔被称作标准具的自由光谱范围(FSR),它由下式给出:
其中是最近峰值的中心波长。
用自由光谱范围除以透射率函数的半高宽(峰值高度一半时的透射峰宽度),得到的值称作精细度(Finesse):
- .
对于较高的反射比(),精细度通常可近似为
从这个公式可知反射比越高时标准具的精细度越高,对应其透射峰越锐利。此外标准具的品质因数等于谐振频率和半高宽的比值,因此精细度也正比于品质因数,这意味着精细度代表了谐振腔的耗散,精细度越高说明谐振腔的耗散越低。
严格意义上的法布里-珀罗干涉仪与标准具的区别在於:干涉仪中两块玻璃板的间隔长度是可调的,从而能够控制不同波长的色光的透射率;并由于透射率还和入射光的倾角有关,通常干涉仪本身也是可旋转的。
干涉条纹[编辑]


如前所述,对单色扩展光源,当相邻两束光之间的光程差为波长的整数倍时,透射率函数有最大值1,此时如在透射光的传播方向上垂直放置一透镜,则在其焦平面上会出现等倾干涉的亮条纹:
通常当透镜光轴垂直于屏时,等倾干涉的条纹是一组同心圆,圆心对应着正入射透射光的焦点。此时由于是正入射,,上面的有最大值:
一般情况下不是整数,如将其整数部分设为,小数部分设为,即,则从中心亮纹数起,外圈第个亮纹的角半径为
从而圆条纹的直径满足
其中是透镜焦距。
应用[编辑]
- 法布里-珀罗干涉仪最常见的应用之一是二项色性滤镜,它是利用物理气相沉积(PVD)方法将一组标准具薄膜镀在光学器件表面。相比于吸收滤镜,这种光学滤镜往往具有更精确的反射和透射频带,特别是当设计恰当时,它们不会像吸收滤镜那样容易造成升温,因为它们可以反射掉那些不必要的波长的色光。二项色性滤镜被广泛应用在光源、相机及天文器材等光学仪器中。
- 在使用波分复用技术的通信网络中,塞取多工机包含了成排的由熔凝石英或金刚石制成的微型标准具。这些标准具边长约为2毫米,嵌入到高精度的微型框架中并发出彩虹色的光泽。这类材料能够保持两个反射镜之间距离的高度稳定性,从而使标准具的谐振频率在环境温度变化时也保持高度稳定。金刚石的优越性在於,它具有更好的导热性而仍拥有较低的热膨胀系数。2005年起,有些通信仪器公司开始采用光纤本身作为固态标准具,这种设计的好处是减少了大部分嵌入、准直和冷却带来的困难。
- 光学波长计通常可由多至五台法布里-珀罗干涉仪的组合来构成,这些干涉仪的共振频率两两具有10倍的间隔。待测光束被一面圆柱透镜发散后,它在这些法布里-珀罗干涉仪中发生各自的干涉,所产生的亮纹的间距则被一台CCD相机所记录,由此可以确定入射光的波长。
- 当激光谐振腔采用平行平面腔的结构时,它可认为是一种法布里-珀罗干涉仪,虽然对於很多激光器而言,其中一面反射镜的反射比可非常接近100%,从而这种谐振腔更像是一种Gires–Tournois干涉仪。半导体激光器有时会采用法布里-珀罗干涉仪的几何结构。
- 法布里-珀罗标准具可用来产生单模激光。在没有标准具的情况下,激光器产生的激光频谱会出现展宽,从而使谐振腔内的激光产生多种模式。使用标准具后,在精细度及自由光谱范围都适当的情形下可以抑制其他模式的产生,使谐振腔内的激光工作在单模情形下。
- 在光谱学中法布里-珀罗标准具可以使光谱仪的分辨本领得到显著提升,从而可以分辨出波长差极细微的光谱线,例如塞曼效应。
- 在天文学中法布里-珀罗标准具可以用来作为一种窄频滤镜,从原子跃迁的多条谱线中过滤出所需的谱线并使之成像,最常见的例子是太阳的H-α线以及Ca-K线。
- 在引力波探测中,采用法布里-珀罗谐振腔可以用来在毫秒量级的时间上储存光子,使其在谐振腔的反射镜之间反复振荡。这种做法增加了引力波探测器的干涉臂的有效长度,从而提高了引力波探测器的灵敏度。这种原理被广泛应用在引力波探测器如LIGO和VIRGO上,它们的构造都是带有法布里-珀罗谐振腔的等臂迈克耳孙干涉仪,干涉臂长度在几千米的量级。同时这些探测器还采用了小型的谐振腔,这些谐振腔通常被称作模式过滤器,它们可用於参与主激光的频率稳定工作。
- 在激光稳频中,法布里-珀罗谐振腔使用低膨胀系数的玻璃,具有稳定的光学长度,用来作为频率稳定的参考。
参考文献[编辑]
- ^ 牛津英语词典
- ^ 佩罗的名字原本是没有重音符号的(Perot),但在科学出版物中他习惯加上重音符号,从而干涉仪的命名也习惯加上重音符号。Métivier, Françoise. Jean-Baptiste Alfred Perot (PDF). Photoniques. September–October 2006, (no. 25) [2010-02-07]. (原始内容 (pdf)存档于2007-11-10) (法语). Page 2: "Pérot ou Perot?"
- ^ Lipson, S.G.; Lipson, H.; Tannhauser, D.S. Optical Physics 3rd. London: Cambridge U.P. 1995: 248. ISBN 0521069262.
- Max Born; Emil Wolf. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (7th Edition) (Hardcover). Cambridge University Press. October 13, 1999: 334 [2010-02-08]. ISBN 0521642221. (原始内容存档于2021-02-20).
- Hernandez, G. Fabry–Pérot Interferometers. Cambridge: Cambridge University Press. 1986. ISBN 0521322383.
- Micron Optics' optical fiber etalons
| ||||||||||||||||||||||||||||||||||||||||||||



























