史密斯-沃特曼演算法

史密斯-沃特曼演算法(Smith-Waterman algorithm)是一種進行局部序列比對(相對於全域比對)的演算法,用於找出兩個核苷酸序列或蛋白質序列之間的相似區域。該演算法的目的不是進行全序列的比對,而是找出兩個序列中具有高相似度的片段。
該演算法由坦普爾·史密斯和米高·沃特曼於1981年提出[1]。史密斯-沃特曼演算法是尼德曼-翁施演算法的一個變體,二者都是動態規劃演算法。這一演算法的優勢在於可以在給定的打分方法下找出兩個序列的最佳的局部比對(打分方法使用了置換矩陣和空位罰分)。該演算法和尼德曼-翁施演算法的主要區別在於該演算法不存在負分(負分被替換為零),因此局部比對成為可能。回溯從分數最高的矩陣元素開始,直到遇到分數為零的元素停止。分數最高的局部比對結果在此過程中產生。在實際運用中,人們通常使用該演算法的最佳化版本[2][3][4]。
歷史
[編輯]生物學上一個基本問題是,一個基因或者蛋白是否和別的基因或者蛋白存在聯絡。蛋白質在序列層次的關聯暗示了其同源性,同時暗示了它們可能有類似的功能。通過分析多個DNA或者蛋白質序列,我們可能會發現一些保守序列和區域。這種基因序列或者蛋白質序列之間關聯性的分析就是通過序列比對來完成的。如今,人們完成了許多不同生物體的基因組分析,獲得了大量的基因和蛋白質序列數據。序列比對能夠向我們揭示某一生物體中蛋白質之間的關聯以及蛋白質在不同生物體中的關聯,從而進一步理解生命和進化。
序列比對起源於1970年。Saul B. Needleman和Christian D. Wunsch於1970提出了一個啟發式的同源演算法[5],稱為尼德曼-翁施演算法。該演算法使用迭代的方法計算出一個矩陣,從而達到全域比對的效果。一些其他的啟發式分析方法也在70年代被提出。Sankoff[6],Reichert[7],Beyer[8]等人提出了一些嚴謹的數學的演算法用來分析序列。然而這些方法通常難以揭示序列的生物學意義。 Sellers提出了一套測量序列距離的方法[9]。沃特曼等於1976年在該方法的基礎上,增加了插入和刪除任意長度片段的方法[10]。該方法解決了如何用最小的基因突變的次數將一個序列轉變成另一個序列的問題。之後,坦普爾·史密斯和米高·沃特曼於1981年提出了史密斯-沃特曼演算法,解決了局部比對問題。
演算法
[編輯]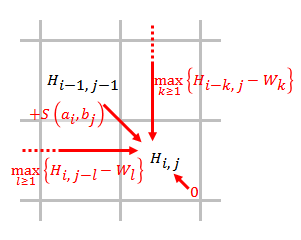
設要比對的兩序列為和,其中和分別為序列和的長度。
- 確定置換矩陣和空位罰分方法
- - 組成序列的元素之間的相似性得分
- - 長度為的空位罰分
- 建立得分矩陣並初始化其首行和首列。該矩陣的大小為行列(注意計數從0開始)。
- 從左到右,從上到下進行打分,填充得分矩陣剩餘部分
- 其中,
- 表示將和比對的相似性得分,
- 表示位於一段長度為的刪除的末端的得分,
- 表示位於一段長度為的刪除的末端的得分,
- 表示和到此為止無相似性。
- 回溯。從矩陣中得分最高的元素開始根據得分的來源回溯至上一位置,如此反覆直至遇到得分為的元素。
解釋
[編輯]史密斯-沃特曼演算法通過字母的匹配,刪除和插入操作,把兩條序列進行排列。實際上插入和刪除都是引入空位的操作(在不同序列上)。序列1上某一位置的插入相當於在序列2上對應位置的刪除。在實際計算中,只需要考慮何時引入空位即可。
該演算法主要分兩步,計算得分矩陣和尋找最佳比對序列。可以簡單描述為:
- 確定置換矩陣及空位罰分方法。置換矩陣賦予每一鹼基對或殘基對匹配或錯配的分數,相同或類似則賦予正值,不同或不相似賦予0分或者負分。空位罰分決定了引入或延長空位的分值。研究者應當根據比對的目的選擇合適的置換矩陣及空位罰分。另外通過比較不同的置換矩陣及空位罰分的組合所帶來的比對結果也可以幫助研究者進行選擇。
- 初始化得分矩陣。得分矩陣的長度和寬度分別為兩序列的長度+1。其首行和首列所有元素均設為0。額外的首行和首列得以讓一序列從另一序列的任意位置開始進行比對,分值為零使其不受罰分。
- 打分。對得分矩陣的每一元素進行從左到右、從上到下的打分,考慮匹配或錯配(對角線得分),引入空位(水平或垂直得分)分別帶來的結果,取最高值作為該元素的分值。如果分值低於0,則該元素分值為0。打分的同時記錄下每一個分數的來源用來回溯。
- 回溯。通過動態規劃的方法,從得分矩陣的最大分值的元素開始回溯直至分數為0的元素。具有局部最高相似性的片段在此過程中產生。具有第二高相似性的片段可以通過從最高相似性回溯過程之外的最高分位置開始回溯,即完成首次回溯之後,從首次回溯區域之外的最高分元素開始回溯,以得到第二個局部相似片段。
與尼德曼-翁施演算法的比較
[編輯]
史密斯-沃特曼演算法為局部比對演算法,用於找出兩序列中最相似的區域。尼德曼-翁施演算法為全域比對演算法,用於完整匹配兩個序列。這兩種演算法的目不同,因此研究者在選擇演算法時要根據實際需求來決定。
兩種演算法都使用了置換矩陣,空位罰分,得分矩陣,以及回溯的方法,具有一定的相似度。然而,史密斯-沃特曼演算法與尼德曼-翁施演算法的三個主要區別在於:
| 史密斯-沃特曼演算法 | 尼德曼-翁施演算法 | |
|---|---|---|
| 初始化階段 | 第一行和第一列全填充為 0 | 首行和首列需要考慮空位罰分 |
| 打分階段 | 若得分為負,則分數為零 | 得分可以為負 |
| 回溯階段 | 從最高分開始,回溯直至得分為 0 | 從右下角開始,回溯至左上角 |
其中,打分階段分數不為負是非常重要的一點區別。它使得對序列局部的比對成為可能。當任何位置分數低於0,即表示此前的序列不具有相似性;而此時將此元素分數設為0,即達到了「重設」的效果,使得從此位置開始的比對不受之前位置的影響。初始化階段的區別使得史密斯-沃特曼演算法中從一序列任意位置開始匹配另一序列不受罰分,而尼德曼-翁施演算法因為要匹配完整的序列,所以兩端的空位也需要罰分。
置換矩陣
[編輯]每一鹼基對或殘基對匹配或錯配的分數通常用一矩陣表示,稱為置換矩陣。基本的置換矩陣為匹配則加分,錯配則扣分。以核苷酸序列為例,若匹配為+1,錯配為-1,則置換矩陣為:
| A | G | C | T | |
|---|---|---|---|---|
| A | 1 | -1 | -1 | -1 |
| G | -1 | 1 | -1 | -1 |
| C | -1 | -1 | 1 | -1 |
| T | -1 | -1 | -1 | 1 |
該置換矩陣可以表示為:
不同的鹼基對或殘基對可以有不同的分數以適應於特定的場合。
氨基酸序列比對的置換矩陣一般更加複雜。通常性質相似的殘基對具有正分數,反之,不相似的具有負分數。此外,殘基對的相似或不相似程度決定了分數的大小。參見PAM,BLOSUM。
空位罰分
[編輯]當鹼基對或殘基對之間匹配會導致更低分數時,需要空位的引入,即讓鹼基或殘基與空位匹配。空位罰分決定了插入或者刪除的分值。最基本的空位罰分方式為每次插入或者刪除的得分相同。然而在生物學上,兩序列之間一般存在着具有不同相似度的區域。另外,單個基因突變事件可能導致一長串空位的插入。因此,一個連續的較長的空位優於多個分散的小的空位。雖然多個分散的小的空位可以產生更多匹配,但一個連續的較長的空位代表這個區域只在一個序列中出現,使用後者可以避免為了得到高分而過度匹配這段序列。實現該方法只需要引入空位起始罰分和空位延長罰分的概念。空位起始罰分通常高於空位延長罰分。例如EMBOSS Water (頁面存檔備份,存於互聯網檔案館)的預設參數為空位起始罰分=10,空位延長罰分=0.5。
實際應用中空位罰分方法有多種(參見空位罰分),此處詳細介紹這兩種最常見的方法。設為空位罰分函數,其中為空位長度:
空位權值恆定模型
[編輯]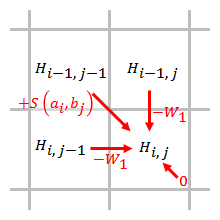
該模型空位的罰分正比於空位的長度。為單個空位的罰分。使用該模型時,原史密斯-沃特曼演算法可簡化為:
此時該演算法步數為,和分別為兩序列的長度。在對某一位置考慮空位罰分時,只需考慮相鄰的上方的和左側的位置,而不需考慮整列和整行。
空位延伸罰分模型
[編輯]
該模型考慮空位起始罰分和空位延長罰分,其中為開始空位的罰分,為每次延長空位的罰分。例如,一個長度為2的空位的罰分為。未經最佳化的該模型的演算法步數為。Gotoh將該演算法的步數最佳化至[2],然而,最佳化後的方法只能找出一個局部比對結果,並且並不保證能成功獲得結果[3]。Altschul進一步最佳化了Gotoh的演算法,在保持複雜度不變的情況下解決了Gotoh演算法的不足[3]。Myers和Miller指出,Gotoh和Altschul的演算法忽視了Hirschberg在1975年提出的線上性空間內進行序列比對的方法[11],並在改進的演算法中運用了該方法[4]。Myers和Miller的演算法僅使用空間,為較短的序列的長度。
空位罰分例子
[編輯]以兩序列TACGGGCCCGCTAC和TAGCCCTATCGGTCA進行比對為例,分別考慮兩種模型。
當使用空位權值恆定模型時,即不考慮空位起始和延長的區別,得到如下結果(置換矩陣為DNAfull,空位起始和延長均為1.0,其他參數為預設):
TACGGGCCCGCTA-C || | || ||| | TA---G-CC-CTATC 总得分为39.0
當使用空位延伸罰分模型時,設空位起始罰分為5.0,空位延長罰分為1.0時,得到如下結果:
TACGGGCCCGCTA || ||| ||| TA---GCC--CTA 总得分为27.0
可以看出,空位延伸罰分模型雖然總分略低,但考慮空位起始罰分和空位延長罰分能夠有效避免多個小的空位。
得分矩陣
[編輯]得分矩陣的作用是對兩序列中兩兩位置進行打分以逐步記錄最佳比對。動態編程的思想體現於此。最終的最佳局部比對結果是由逐步擴充當前位置最佳比對結果來實現的(即通過作出一系列的對如何比對當前位置可以得到更高分數的決定來得到最終結果)。矩陣的長度和寬度分別為兩序列長度+1。額外的首行和首列是為了讓序列的末端可以和空位匹配。首行和首列均設為0。以CTCAA和GGTCA為例,初始得分矩陣為:
| - | - | C | T | C | A | A |
|---|---|---|---|---|---|---|
| - | 0 | 0 | 0 | 0 | 0 | 0 |
| G | 0 | |||||
| G | 0 | |||||
| T | 0 | |||||
| C | 0 | |||||
| A | 0 |
例子
[編輯]以序列TGTTACGG和GGTTGACTA為例。使用如下參數:
- 置換矩陣:
- 空位罰分:
初始化得分矩陣,並進行打分。如下圖所示。該圖展示了該得分矩陣前三個元素的打分過程。黃色代表當前正在考慮的兩個鹼基。紅色代表該位置得分的來源。

打分完成後的得分矩陣如左下圖所示。其中藍色代表最高分元素。注意某些元素有不止一種得分來源,這樣在回溯過程中會產生多個路徑。如果有多個相同的最高分,則應當考慮每個最高分的回溯。回溯過程見右下圖。局部最相似序列在從最高分回溯的過程中自右向左產生。
 |
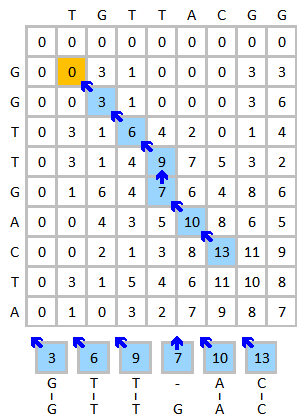 |
| 完成後的得分矩陣及最高分(藍色) | 回溯過程以及比對結果 |
該例的結果為:
G T T - A C | | | | | G T T G A C
相關連結
[編輯]參考資料
[編輯]- ^ Smith, Temple F.; and Waterman, Michael S. Identification of Common Molecular Subsequences (PDF). Journal of Molecular Biology. 1981, 147: 195–197 [2016-04-26]. PMID 7265238. doi:10.1016/0022-2836(81)90087-5. (原始內容存檔 (PDF)於2016-01-21).
- ^ 2.0 2.1 O. Gotoh. An Improved Algorithm For Matching Biological Sequences. Journal of Molecular Biology. 1982, 162: 705–708. doi:10.1016/0022-2836(82)90398-9.
- ^ 3.0 3.1 3.2 Stephen F. Altschul; and Bruce W. Erickson. Optimal Sequence Alignment Using Affine Gap Costs. Bulletin of Mathematical Biology. 1986, 48: 603–616. doi:10.1007/BF02462326.
- ^ 4.0 4.1 Eugene W. Myers; and Webb Miller. Optimal alignments in linear space. Computer applications in the biosciences. 1988, 4: 11–17. doi:10.1093/bioinformatics/4.1.11.
- ^ Saul B. Needleman; and Christian D. Wunsch. A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology. 1970, 48: 443–453. doi:10.1016/0022-2836(70)90057-4.
- ^ Sankoff D. Matching Sequences under Deletion/Insertion Constraints. Proceedings of the National Academy of Sciences of the United States of America. 1972, 69: 4–6. doi:10.1073/pnas.69.1.4.
- ^ Thomas A. Reichert; Donald N. Cohen; and Andrew K.C. Wong. An application of information theory to genetic mutations and the matching of polypeptide sequences. Journal of Theoretical Biology. 1973, 42: 245–261. doi:10.1016/0022-5193(73)90088-X.
- ^ William A. Beyer; Myron L. Stein; Temple F. Smith; and Stanislaw M. Ulam. A molecular sequence metric and evolutionary trees. Mathematical Biosciences. 1974, 19: 9–25. doi:10.1016/0025-5564(74)90028-5.
- ^ Peter H. Sellers. On the Theory and Computation of Evolutionary Distances. Journal of Applied Mathematics. 1974, 26: 787–793. doi:10.1137/0126070.
- ^ M.S Waterman; T.F Smith; and W.A Beyer. Some biological sequence metrics. Advances in Mathematics. 1976, 20: 367–387. doi:10.1016/0001-8708(76)90202-4.
- ^ D. S. Hirschberg. A linear space algorithm for computing maximal common subsequences. Communications of the ACM. 1975, 18: 341–343. doi:10.1145/360825.360861.


































