跳转到内容

星形多面体

维基百科，自由的百科全书

在几何学中，星形多面体是一种非凸多面体，通常表示外表有如星形一般的多面体[1]，其可以视为星形多边形之于多边形在三维空间中的类比。[2]

种类

[编辑]

一般星形多面体可以分为两种不同的形式：

  • 以重复方式自我相交[3]的多面体。
  • 交替地重复凸与凹或鞍形顶点之凹多面体。在数学中，这种结构是星形域的示例[4]。更白话的说法则是外观有明显凸出之顶点的立体[5][6]。

自相交多面体

[编辑]

一般数学上研究的星形多面体通常是正图形、半正图形或均匀图形以及其对偶多面体[7]（如均匀多面体对偶），同时，这些立体通常都会有面自我相交的情况。[8]

星形正多面体

[编辑]
主条目：星形正多面体

星形正多面体是面或边有与同一立体中其他面或边相交的情况的正多面体。其通常会具有星形的面或星形的顶点图，即如星形般相交的一系列面构成的多面角。[1]

星形正多面体

星形均匀多面体

[编辑]

星形均匀多面体是面或边有与同一立体中其他面或边相交的情况的均匀多面体。

部分的星形均匀多面体
均匀多面体 对偶多面体

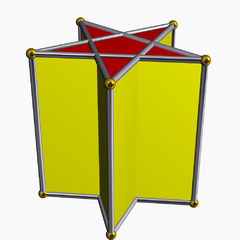五角星柱（英语：pentagrammic prism）是一种星形均匀柱体（英语：Prismatic uniform polyhedron），由两个五角星面和5个正方形面组成。
五角星柱的对偶多面体是双五角星锥（英语：pentagrammic dipyramid），同时也是一种星形多面体，由10个等腰三角形组成。

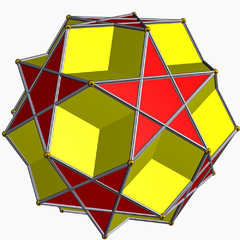截半大十二面体是一种由五边形和五角星组成的星形均匀多面体[9]
截半大十二面体的对偶多面体为内侧菱形三十面体，同时也是一种星形多面体，由30个菱形组成[10]

星形域的多面体

[编辑]
教堂的摩拉维亚星。

一些没有自相交情况的多面体同样也可以算是星形多面体，这类多面体通常是交替地重复凸与凹或鞍形顶点之凹多面体，这类多面体是星形域的实例之一[11]。许多自相交的星形多面体皆可以找到一个外观相同的非自相交多面体，但其在抽象几何学中具有不同的结构，例如截半大十二面体以及一个不包含内部结构的截半大十二面体[12][13][14]，同时也有可能有2个外观相同但结构不同的星形多面体，例如内侧三角六边形二十面体与大三角六边形二十面体[15][16][17][18]。

这种星形多面体通常用于各种建筑的装饰中，尤其在一些宗教建筑中[19][20]，例如在巴洛克式教堂、匈牙利教堂和其他宗教建筑物上，星形多面体被视为建造教堂的教宗的象征，同时，也可以在来当作装饰品，如摩拉维亚星（英语：Moravian star）。[21]

参见

[编辑]

参考文献

[编辑]
  1. ^ 1.0 1.1 前川淳. 摺紙幾何學：60種特殊摺紙. 科学视界. 世茂出版社. 2018-04-02. ISBN 9789578799165. 
  2. ^ はじめての多面体おりがみ: 考える頭を作ろう. Heart warming life series. 日本ヴォーグ社. 2001: 84. ISBN 9784529035477. 
  3. ^ Paul Bourke; Polygons and meshes:Surface (polygonal) Simplification （页面存档备份，存于互联网档案馆） 1997. (retrieved May 2016)
  4. ^ Ian Stewart, David Tall, Complex Analysis. Cambridge University Press, 1983, ISBN 0-521-28763-4, MR0698076
  5. ^ 心、星、球. etoe.tc.edu.tw. [2019-09-27]. （原始内容存档于2019-09-27）. 
  6. ^ 巫翌婕, 林欣仪, 赖萤葶, 吴宜真. 凸起而遇－關於星形多面體的研究 (PDF). shs.edu.tw. [2019-09-27]. （原始内容存档 (PDF)于2019-09-27）. 
  7. ^ Weisstein, Eric W. (编). Star Polyhedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
  8. ^ 三村 文武, 岩下 有里. ユニットによる星形多面体の構成 (PDF). 広岛経済大学研究论集 (広岛経済大学). 2011年9月, 32 (2): 23––34 [2019-09-27]. （原始内容存档 (PDF)于2019-09-27）. 
  9. ^ David A. Richter. The Dodecadodecahedron and the Golay Code. wmich.edu. [2019-09-27]. （原始内容存档于2018-10-18）. 
  10. ^ Versi-Regular Polyhedra: Medial Rhombic Triacontahedron. dmccooey.com. （原始内容存档于2016-03-24）. 
  11. ^ C.R. Smith, A characterization of star-shaped sets, American Mathematical Monthly, Vol. 75, No. 4 (April 1968). p. 386, MR0227724,
    JSTOR 2313423
  12. ^ Geometric Model by Dick Holl, a Student of A.Harry Wheeler, Dodecadodecahedron. americanhistory.si.edu. [2019-09-27]. （原始内容存档于2019-09-26）. 
  13. ^ Paper Dodecadodecahedron. polyhedra.net. 
  14. ^ Dodecadodecahedron. polyhedr.com. [2019-09-27]. （原始内容存档于2019-09-26）. 
  15. ^ great triambic icosahedron. bulatov.org. （原始内容存档于2016-03-03）. 
  16. ^ Weisstein, Eric W. (编). Great Triambic Icosahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
  17. ^ Weisstein, Eric W. (编). Medial Triambic Icosahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
  18. ^ Guy's polyhedra pages. Some lost stellations of the icosahedron. steelpillow. 2006-07-11. （原始内容存档于2016-03-13）.  Index Number: 303, Precursor: BnGn, Du Val symbol: De2f2
  19. ^ Tarnai, T.; Krähling, J.; and Kabai, S., "Star Polyhedra: from St Mark's Basilica in Venice to Hungarian Protestant Churches." (PDF), Paper ID209 in Proc. of the IASS 2007, Shell and Spatial Structures: Structural Architecture-Towards the Future Looking to the Past. Venice (Italy: University of IUAV), 2007 [永久失效链接]
  20. ^ Tarnai, T.; Krähling, J.; and Kabai, S., "Star Polyhedra on Hungarian Protestant Churches.", In Proc. of the 13th International Conference on Geometry and Graphics (Ed. G. Weiss). Dresden (Germany: Technical University of Dresden, Germany), 2008 
  21. ^ "The Moravian Star". [2007-10-08]. （原始内容存档于2007-10-08）. 


外部链接

[编辑]
检索自“https://zh.wikipedia.org/w/index.php?title=星形多面體&oldid=79894071”