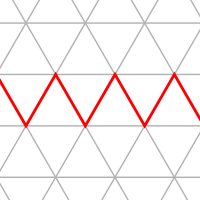
三角形半无限边形镶嵌
 | ||
| 类别 | 均匀星形镶嵌图 | |
|---|---|---|
| 识别 | ||
| 名称 | 三角形半无限边形镶嵌 trigonal hemiapeirogonal tesselation | |
| 鲍尔斯缩写 | tha | |
| 数学表示法 | ||
| 威佐夫符号 | 3/2 3 | ∞ | |
| 组成与布局 | ||
| 面的种类 | 正三角形 无限边形 | |
| 顶点图 | ∞.3.∞.3/2 | |
| 对称性 | ||
| 对称群 | p6m | |
| 图像 | ||
| ||
三角形半无限边形镶嵌(trigonal hemiapeirogonal tesselation)是一种平面镶嵌图,由三角形和无限边形组成。[1]其外观与截半六边形镶嵌相似,差别在于截半六边形镶嵌有三角形面和六边形面,而三角形半无限边形在外观上仅有三角形面,剩余的六边形为孔洞。[2]这个几何结构可以视为半多面体的一种广义的形式。[3][1]
性质
[编辑]三角形半无限边形镶嵌与拟正半多面体类似,可以视为一种退化的半多面体,[注 2]构造自截半六边形镶嵌,并取其中的三角形面和作为半球面的无限边形面构成。[3]
-
三角形半无限边形镶嵌
三角形半无限边形镶嵌由正三角形和无限边形组成,每个顶点都是2个三角形和2个无限边形的公共顶点,并且以无限边形、三角形、无限边形、反向相接的三角形的方式排列,在顶点布局中可以用∞, 3, ∞, 3/2来表示[3]。
顶点坐标
[编辑]三角形半无限边形镶嵌与截半六边形镶嵌共用相同的顶点坐标[2]。若对应的三角形半无限边形镶嵌边长为单位长,则对应的顶点坐标可以透过截半六边形镶嵌的对称性推出。对任意整数和,三角形半无限边形镶嵌的顶点坐标可以表示为:[6]
双三角形半无限边形镶嵌
[编辑] | ||
| 类别 | 均匀星形镶嵌图 | |
|---|---|---|
| 识别 | ||
| 名称 | 双三角形半无限边形镶嵌 ditrigonary trigonal hemiapeirogonal tesselation | |
| 鲍尔斯缩写 | ditatha | |
| 数学表示法 | ||
| 威佐夫符号 | 3/2 | 3 ∞ | |
| 组成与布局 | ||
| 面的种类 | 三角形 无限边形 | |
| 顶点图 | [(3,∞)3]/2 = [(3/2,∞)3] | |
| 对称性 | ||
| 对称群 | p6m | |
| 图像 | ||
| ||
有另一种由三角形与无限边形构成的平面镶嵌图称为双三角形半无限边形镶嵌(ditrigonary trigonal hemiapeirogonal tesselation)。这种镶嵌图的外观与三角形镶嵌类似,但交错地缺少了部分的三角形,因此又称交错三角形镶嵌(alternate triangular tiling)。[7]
性质
[编辑]双三角形半无限边形镶嵌与拟正半多面体类似,可以视为一种退化的半多面体,[注 2]构造自施莱夫利符号计为h{6,3}的三角形镶嵌,并从这种镶嵌中的两种面——原始三角形面或h{6,3}变换结果的三角形面中取其中以种三角形面和作为半球面的无限边形面构成。[3]
-
h{6,3}
-
取其中一种三角形面构成的双三角形半无限边形镶嵌
-
取另种三角形面构成的双三角形半无限边形镶嵌
双三角形半无限边形镶嵌每个顶点都是3个三角形和3个无限边形的公共顶点。特别地,由于双三角形半无限边形镶嵌的顶点图环绕顶点2次,因此这个顶点图在顶点布局符号中要使用除以二的符号来表示:(∞, 3, ∞, 3, ∞, 3 ) / 2,亦可以表示为[(3,∞)3]/2或[(3/2,∞)3] 。[7]
相关多面体与镶嵌
[编辑]三角形半无限边形镶嵌与截半六边形镶嵌和六边形半无限边形镶嵌共用相同的顶点排列。[2][8]
-
三角形半无限边形镶嵌与截半六边形镶嵌和六边形半无限边形镶嵌的顶点排列
-
三角形半无限边形镶嵌
-
六边形半无限边形镶嵌
双三角形半无限边形镶嵌与正三角形镶嵌和皮特里三角形镶嵌共用相同的顶点排列。[7][9]
-
三角形半无限边形镶嵌与截半六边形镶嵌和六边形半无限边形镶嵌的顶点排列
-
h{6,3}
-
双三角形半无限边形镶嵌的一种形式
-
双三角形半无限边形镶嵌的另一种形式
-
皮特里三角形镶嵌
皮特里三角形镶嵌
[编辑] | ||
| 类别 | 均匀星形镶嵌图 | |
|---|---|---|
| 名称 | 皮特里三角形镶嵌 Petrial triangular tiling | |
| 数学表示法 | ||
| 施莱夫利符号 | {3,6}π {∞,6}3 | |
| 组成与布局 | ||
| 面的种类 | 扭歪无限边形 | |
| 图像 | ||
| ||
皮特里三角形镶嵌是正三角形镶嵌的皮特里对偶,可以透过将原有三角形镶嵌上取皮特里多边形构成,换句话说,皮特里三角形镶嵌为由正三角形镶嵌的皮特里多边形构成的几何结构。[10]
-
组成皮特里三角形镶嵌的扭歪无限边形
皮特里三角形镶嵌可以视为一种由扭歪无限边形组成的广义正多面体[11],对应的扭歪内角为60度,且每个顶点都是6个扭歪无限边形的公共顶点,对应的皮特里多边形为三角形,这样的拓朴结构在施莱夫利符号中可以用{∞,6}3来表示。[10]
-
皮特里三角形镶嵌的每个顶点都是6个扭歪无限边形的公共顶点
复无限边形
[编辑]| 三元边十二角无限边形 | |
|---|---|
 淡蓝色的三角形为三元边 | |
| 类型 | 复数空间无限边形 |
| 边 | 无穷个3{} |
| 顶点 | 无穷 |
| 施莱夫利符号 | 3{12}2 |
| 考克斯特符号 | |
| 鲍尔斯缩写 | tha |
| 特性 | 正、复 |
复无限边形是指边数为正无穷大的复多边形。有两种复无限边形顶点排布与三角形半无限边形镶嵌及截半六边形镶嵌相同。复无限边形的一个特点是其边可以包含多于2个顶点,如三元边。正复无限边形在施莱夫利符号中可以记为p{q}r,其中p、q、r满足等式1/p + 2/q + 1/r = 1。在这个符号中,p表示每个边由p个顶点构成,顶点的排列方式同于正多边形;r表示其顶点图为r边形。[12]

|

|
| 3{12}2 |
6{6}2 |
|---|
参见
[编辑]注释
[编辑]参考文献
[编辑]- ^ 1.0 1.1 Grünbaum, Branko; Shephard, G. C. Tilings and Patterns. W. H. Freeman and Company. 1987. ISBN 0-7167-1193-1. (Star tilings section 12.3)
- ^ 2.0 2.1 2.2 Klitzing, Richard. trigonal hemiapeirogonal tesselation: tha. bendwavy.org. [2021-09-06]. (原始内容存档于2021-09-24).
- ^ 3.0 3.1 3.2 3.3 Jim McNeill. Infinite and Semi-infinite tessellations. orchidpalms.com. [2021-08-01]. (原始内容存档于2020-02-25).
- ^ Versi-Regular Polyhedra. dmccooey.com. [2021-08-01]. (原始内容存档于2021-07-30).
- ^ Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P., Uniform polyhedra, Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society), 1954, 246 (916): 401–450, ISSN 0080-4614, JSTOR 91532, MR 0062446, doi:10.1098/rsta.1954.0003
- ^ Nagy, Benedek and Abuhmaidan, Khaled. A continuous coordinate system for the Plane by triangular symmetry. Symmetry (Multidisciplinary Digital Publishing Institute). 2019, 11 (2): 191.
- ^ 7.0 7.1 7.2 Klitzing, Richard. ditrigonary trigonal hemiapeirogonal tesselation: ditatha. bendwavy.org. [2021-09-06]. (原始内容存档于2021-09-24).
- ^ Klitzing, Richard. hexagonal hemiapeirogonal tesselation: hoha. bendwavy.org. [2021-09-06]. (原始内容存档于2021-09-24).
- ^ Klitzing, Richard. triangular tiling: trat. bendwavy.org. [2021-09-06]. (原始内容存档于2021-08-09).
- ^ 10.0 10.1 McMullen, P., Schulte, E. Regular Polytopes in Ordinary Space. Discrete & Computational Geometry. 1997-06-01, 17 (4): 449-478 [2021-09-06]. ISSN 1432-0444. doi:10.1007/PL00009304. (原始内容存档于2018-06-03).
- ^ Andreas W. M. Dress. A combinatorial theory of Grünbaum's new regular polyhedra, Part II: Complete enumeration. Aequationes Mathematicae. 1985-12, 29 (1): 222–243 [2021-09-24]. ISSN 0001-9054. doi:10.1007/BF02189831. (原始内容存档于2021-09-26) (英语).
- ^ Coxeter, H.S.M. Regular Complex Polytopes 2nd. Cambridge University Press. 1991: 111–2, 136. ISBN 9780521394901.
外部链接
[编辑]- 关于皮特里三角形镶嵌,可参考YouTube上的《普通空间中的48种正多面体》(英文)