跳至內容

固定的星星

維基百科，自由的百科全書
夜空中的星星似乎附著在黑暗的 天穹背景上。
約翰尼斯·克卜勒1596 年的「神秘的宇宙誌」。克卜勒對宇宙的日心說，包含一個最外層的「恆星圈」，或固定恆星球體。

固定的星星（拉丁語：stellae fixae）在天文學中是固定的發光點，主要是恆星，它們在黑暗夜空的背景中，似乎彼此之間沒有相對移動。這與那些肉眼可見的光，即行星和彗星形成對比，它們似乎在那些「固定的星星」之間緩慢移動。

固定的星星包括除太陽之外，所有發出可見光而肉眼可見的恆星，以及光度微弱的銀河。由於它們用肉眼觀察時看起來像星星，少數可見的單個星雲和其他深空天體也被算在固定的星星中。在最佳條件下，肉眼可以看到大約6,000顆星星。

「固定的星星」一詞是用詞不當（英語：Misnomer）的短語，因為這些天體實際上並不是相對於彼此或地球固定不動的。由於它們與地球的巨大距離，這些物體在天空中的移動速度似乎很慢，以至於在人類的時間尺度上，它們的相對位置變化幾乎是不可察覺的，除非用現代儀器仔細檢查，如望遠鏡，才可以揭示它們的自行。因此，它們可以被認為是「固定的」，用於許多目的，如導航、恆星製圖、[天體測量學|天體量測]]和計時。

由於天體的距離很遠，人類視覺無法感知太空的三維深度，給人的印象是所有恆星和其他太陽系外天體（英語：Extrasolar object）都與觀察者等距。從歷史上看，固定的星星通常被認為存在於一個巨大的天球或蒼穹（英語：Firmament）上，它每天圍繞地球旋轉，因此它被稱為「固定星星的球體」，它充當了整個宇宙的假定極限。許多世紀以來，「固定的星星」一詞是那個天球的同義詞。

在許多文化中，人們都想像過最亮的星星會形成星座，這是天空中明顯的圖片，似乎是持久的，也被認為是「固定的」。這樣的星座已經使用了幾個世紀，今天仍然被專業人士和業餘天文學家用於識別夜空區域。

包括固定的星星的天文模型

[編輯]

畢達哥拉斯學派

[編輯]

畢達哥拉斯學派的哲學家們對宇宙的結構持有多種不同的觀點，但每種觀點都包括一個恆星球體作為其邊界。菲洛勞斯（英語：Philolaos，約西元前5世紀）提出了一個宇宙：其中心有人類看不見的中心火。所有的行星、月球、太陽和恆星都圍繞著這個中心火旋轉，而地球是離它最近的物體[1]。在這個系統中，恆星被包含在最遠的球體中，球體也在旋轉，但速度太慢，無法觀察到運動。 相對的，恆星的運動是由地球圍繞中心火的運動來解釋[1]。

另一位畢達哥拉斯學派的錫拉庫紮人愛克範特（英語：Ecphantos）（Ecphantos（英語：Ecphantos），約西元前400年）提出了一個與菲洛勞斯非常相似的系統，但沒有中央火。取而代之的是這個宇宙以地球為中心，地球固定在中心，但繞著一個軸旋轉，而月球、太陽和行星則繞著地球旋轉[1]。這個系統的最終邊界是一個固定的恆星球體，人們認為恆星的運動是由地球的自轉引起的[1]。

柏拉圖

[編輯]

柏拉圖（西元前429-347年）的宇宙以一個完全靜止的地球為中心，由一系列同心球體構成。這個系統外層的球由火組成，並包含了所有的行星（根據柏拉圖的說法，也包括月球和太陽）。這個球體的最外層是恆星的位置[2]，這個火球帶著恆星繞地球旋轉。這一信念對柏拉圖的整個體系都非常重要：恆星的位置固定在火球中。恆星的位置被用作所有天體運動的參攷，並被用來創造柏拉圖關於行星具有多種運動的想法[3]。

歐多克索斯

[編輯]

柏拉圖的學生多尼斯的歐多克索斯，出生於西元前400年左右[4]，是一名數學家和天文學家。他根據自己的數學家背景，建立了最早的同心球體（英語：Concentric spheres）行星系統模型之一。歐多克索斯的模型是地心的，地球是一個位於系統中心的靜止球體，被27個旋轉球體包圍著[4]。最遠的球體承載著恆星，他宣稱恆星固定在球體內。因此，儘管恆星被它們所佔據的球體圍繞地球移動，但它們本身並沒有移動，所以被認為是固定的[5]。

亞里斯多德

[編輯]

亞里斯多德，生活在西元前384年至西元前322年[4]，他研究並發表了與柏拉圖類似的思想，並以歐多克索斯的體系為基礎，但他通過西元前350年左右寫的《形上學》和《論天（英語：On the Heavens）》對其進行了改進[4]。他聲稱所有事物都有某種運動管道（包括「天體」和行星），但他否認這種運動可能是由真空引起的，因為那樣的話，物體會運動得太快，且沒有明確的方向[4]。他說，一切都是被某種東西移動的，並開始探索一個類似於重力的概念。他是最早利用日食觀測和其它行星相對於地球的運動來論證（並證明）地球是圓的人之一[4]。他接著得出結論，大多數行星都是在天球體（英語：Celestial spheres）以圓周運動運行著。

他的宇宙是地心的，以地球為中心，被一層水和空氣包圍，而水和空氣又被一層火包圍，火充滿了整個空間，直到到達月球[5]。亞里斯多德還提出了第五種元素，稱為「乙太」，據稱它構成了太陽、行星和恆星[4]。然而，亞里斯多德認為，雖然行星在旋轉，但恆星仍然是固定的。他的論點是，如果這樣一個巨大的物體在移動，那麼肯定有證據可以從地球上看到[6]。然而，人們無法聽到恆星的運動，也無法真正看到它們的進展，因此亞里斯多德得出結論，雖然它們可能會被行星移動，但它們不會自己移動。他在《論天》一書中寫道：「如果恆星的身體以空氣或火焰的形式運動……它們產生的譟音將不可避免地是巨大的，而事實就是這樣，它會到達並粉碎地球上的東西。」[7]。他提出的恆星可能被攜帶，但它們是固定的，不會自主移動或旋轉的理論在一段時間內被廣泛接受。

阿里斯塔克斯

[編輯]

薩摩亞的阿里斯塔克斯（西元前3世紀），提出了一個早期的日心說宇宙，這啟發了哥白尼後來的工作。在他的模型中，太陽完全靜止，位於中心，所有行星都圍繞它旋轉[8]。行星之外是恆星的球體，也是靜止的。 除了日心說之外，這個系統還提出了另外兩個獨特的想法：地球每天旋轉以創造白天、黑夜和其它天體的感知運動，而其邊界處的恆星球體距離其中心非常遙遠[9]。由於觀測到的恆星沒有視差，因此必須假設這種巨大的距離，這只能用地心引力或巨大的距離來解釋，這些距離產生的視差太小而無法量測。

克勞狄烏斯·托勒密

[編輯]

托勒密，100-175 AD[5]，通過他的數學模型和他的書《數學通論》（通常被稱為《天文學大成》）總結了關於宇宙的思想[4]。這本書寫於西元150年左右，托勒密宣稱，恆星之間的相對位置和距離不會因天空的旋轉而改變[5]。他利用日食來計算恆星距離，並根據視差觀測計算月球距離[10]。不久之後，他寫了一篇名為《行星假說》的後續文章[10]。

托勒密使用並撰寫了關於地心系統的文章，極大地借鑒了傳統的亞里斯多德物理學[10]，但他使用了更複雜的裝置，即從幾何學家佩爾格的阿波羅尼斯和天文學家尼西亞的喜帕恰斯的先前著作中借用了均輪和本輪[11]。他宣稱，恆星在其天球內是固定的，但天球本身並不是固定的。因此，這些球體的旋轉解釋了星座全年的微妙運動[5]。

馬爾提亞努斯·卡佩拉

[編輯]

馬爾提亞努斯·卡佩拉（fl.c.410-420）描述了一種改進的地心模型，在該模型中，地球位於宇宙的中心，被月球、太陽、三顆行星和恆星環繞，而水星和金星則繞著太陽旋轉，所有這些都被恆星的球體包圍著[12]。 儘管他很有權威，但他的模式並沒有被廣泛接受；他是七體系（博雅教育）、三藝（語法、邏輯和修辭學）和四術（算術、幾何學、音樂、天文學）的最早開發者之一，這些體系構成了中世紀早期的教育[13]。儘管如此，他的百科全書式著作《論語言學與墨丘利的結合（英語：Martianus Capella# De nuptiis）》（英語：On the Marriage of Philology and Mercurii），也被稱為《論七門學科》（英語：On the seven disciples），在整個中世紀早期都被閱讀、教授和評論，並在中世紀早期和卡洛林文藝復興時期塑造了歐洲教育[14]。

尼古拉·哥白尼

[編輯]

尼古拉·哥白尼 （1473-1543）創造了一個由承載每個天體的球體組成的哥白尼日心說（英語：Copernican heliocentrism）的日心系統[15]。他模型中的最後一個球體是恆星。這個最後的球體在直徑和厚度上都是他的宇宙中最大的。這個恆星球體是完全固定的，因為恆星嵌入球體中，球體本身是不動的[15]。因此，恆星的感知運動是由地球圍繞其軸線的日常自轉造成的。

第谷·布拉厄

[編輯]

第谷·布拉厄（1546-1601）由於其雙重結構，被稱為「地球日心說」[9]。在它的中心是靜止的地球，由月球和太陽繞其運行。然後，行星圍繞太陽旋轉，而太陽圍繞地球旋轉。在所有這些天體之外，是一個由恆星組成的球體[16]。這個球體圍繞靜止的地球旋轉，產生了天空中恆星的感知運動[16]。這個系統有一個有趣的特徵，即太陽和行星不能被包含在固體球體中（它們的球體會碰撞），但恆星被表示為包含在宇宙邊界的固定球體中[16]。

約翰尼斯·克卜勒

[編輯]

約翰尼斯·克卜勒（1571-1630）是一位虔誠的哥白尼主義者，他遵循哥白尼的模型和思想，並對其進行了發展[4]。他也是第谷·布拉厄的助手，他可以在觀測資料庫中查閱贊助人的精確測量值。克卜勒的《神秘宇宙圖》（1596）是對哥白尼系統的有力辯護，它仍然描繪了一幅影像，將最外層的天球標記為「球體恆星修護」，拉丁語表示恆星固定球，這是長期以來對這種球的信仰。

這一觀點後來在他的著作《新天文學》（1609）中被取代，他在書中建立了他的《行星運動定律》[17]，他自己以數學為基礎的「魯道夫星曆表」，是可以顯示行星位置的工作表[10]。克卜勒定律是最終推翻舊的地心（或托勒密的）宇宙理論和模型的轉捩點[18]，這是由他同時代的人，伽利略首次使用望遠鏡所支持的，他也是哥白尼的擁護者。

估計半徑

[編輯]

首先，希臘人和許多其他古代文化一樣，認為天空是一個巨大的圓頂狀結構，距離最高的山脈只有幾米。阿特拉斯的神話述說整個天空都壓在泰坦的肩上[19]。

大約在西元前560年，阿那克西曼德首次提出了一個天體以不同距離旋轉的系統。但錯誤的是，他認為恆星（大約是地球大小的9到10倍）比月球（18-19倍）和太陽（27-28倍）更靠近地球[20]。儘管如此，後來畢達哥拉斯學派的菲洛勞斯在西元前400年左右也構想了一個有軌道體的宇宙[21]，因此，假設恆星至少比月球、太陽和其它行星更遠一點。

與此同時，大約在西元前450年，阿那克薩哥拉是第一位將太陽視為一個巨大物體（比伯羅奔尼撒半島還要大）的哲學家[22]，因此，他認為月球是岩石，所以是不透明的，並且比太陽更靠近地球，從而對日食給出了正確的解釋[23]。就太陽和月球被視為球體而言，由於它們在日食時不會碰撞，這意味著外太空應該有一定的、不確定的深度。

多尼斯的歐多克索斯，大約在西元前380年，他基於以地球為中心的（概念性）同心球體（英語：Concentric spheres）設計了一個行星運動的幾何數學模型[24]，到西元前360年，柏拉圖在他的《蒂邁歐篇》中聲稱，圓形和球體是宇宙的首選形狀，地球位於中心，恆星形成最外層，其次是行星、太陽和月球 [25]。

大約在西元前350年亞里斯多德修改了歐多克索斯的模型，假設球體是物質和晶體[26]。他能夠清楚地表達出大多數行星的球體，然而，木星和土星的球體是相互交叉的。亞里斯多德通過引入一個展開的球體解決了這個複雜問題。通過所有這些裝置，甚至假設行星是恆星狀的，單一的點，恆星的球體應該比以前想像的更遠。

大約在西元前280年，薩摩斯的阿里斯塔克斯提出了關於日新說宇宙可能性的第一次明確討論[27]，通過幾何方法，他估計月球的軌道半徑為60地球半徑，其實際半徑為地球的三分之一。他試圖量測到太陽的距離，雖然不準確，但足以斷言太陽比地球大得多，比月球遠得多。因此，小天體地球必須圍繞大天體太陽運行，而不是相反的狀態[28]。這一推理使他斷言，由於恆星在一年內從地球上看不到明顯的視差，它們一定離地球表面非常非常遠，假設它們離我們的距離都是一樣的，他給出了一個相對的估計。

根據阿里斯塔克斯的日心說（但沒有明確支持），大約在西元前250年，阿基米德在他的著作《數沙者》中計算出以太陽為中心的宇宙的直徑約為10×1014 stadia（以現代單位計算，約為2光年， 18.93×1012 km, 11.76×1012 mi）[29]。

用阿基米德自己的話說：

他（阿里斯塔克斯）的假設是，固定的星星和太陽保持不變，地球在圓周上圍繞太陽旋轉，太陽位於軌道的中間，固定恆星的球體與太陽有著同一中心，如此之大，以至於他假設地球旋轉的圓與固定恆星的距離成比例，就像球體的中心與表面的距離一樣[30]。

大約在西元前210年，佩爾格的阿波羅尼斯顯示了行星視逆行的兩種描述的等價性（假設地心模型）：一種使用偏心率，另一種使用均輪和本輪[11]。

在接下來的一個世紀裏，地球和月球大小和距離的測量方法得到了改進。大約西元前200年埃拉托斯特尼確定地球的半徑大致為6,400 km（4,000 mi）[31]。大約西元前150年喜帕恰斯使用視差來確定到月球的距離大致為380,000 km（236,100 mi）[32]，幾乎與阿里斯塔克斯相匹配。這就規定了地球到月球中心距離的固定恆星球體的最小半徑加上月球的半徑（大約地球半徑的1/3），加上太陽的寬度（至少與月球相同），再加上行星球體的不確定厚度（無論如何都被認為很薄），總共約386,400 km（240,100 mi）。這比阿基米德的計算低2,450萬倍。

地心模型所描述的複雜性。

大約在西元130年，托勒密在他的地心模型中採用了阿波羅尼奧斯的本輪[33]。 本輪被描述為軌道內的軌道。例如，托勒密在觀察金星時聲稱，金星繞地球運行，當它繞地球運行時，它也繞著第二個較小的局部球體繞原始軌道運行（托勒密強調本輪運動不適用於太陽。）。這個裝置必然會放大每個天體，從而使恆星的外層更大。

當學者們應用托勒密的本輪時，他們認為每個行星球體的厚度都足以容納它們[34]。通過將這種嵌套球體模型與天文觀測相結合，學者們計算出了當時普遍接受的到太陽的距離值：大約4 × 106公里（2.5 × 106英里），到宇宙的邊緣：約73 × 106公里（45 × 106英里）[35]，仍然比阿基米德少13萬倍左右。

托勒密在他的《天文學大成》中提出的方法足夠準確，在1,500多年的時間裏基本上沒有爭議[36]。 但在歐洲文藝復興時期，這樣一個巨大的球體在24小時內繞地球完成一次360°旋轉的可能性被認為是不可能的[37]， 這一點是尼古拉斯·哥白尼（英語：Nicholas Copernicus）拋棄幾個世紀以來的地心模型的論點之一。

有史以來給出的最高上限是由猶太天文學家吉爾松尼德（英語：Gersonides）給出的，他在1300年左右估計到恆星的距離不小於159,651,513,380,944地球半徑，按現代單位計算約為100,000光年[38]。這是高估了；儘管在實際的宇宙中，無論是在銀河系（大約寬三倍）還是所有外星系中，都有比這個距離更遠的恆星，但離地球最近的恆星（太陽除外）是半人馬座的比鄰星，大約只有4.25光年。

北歐神話

[編輯]

解釋宇宙的嘗試源於對天空中發現的物體的觀測。歷史上，不同的文化有不同的故事來回答他們所看到的問題。北歐神話起源於北歐，圍繞現代地區斯堪地那維亞和德國北部的地理位置。北歐神話由源自古諾斯語的故事和神話組成，是中世紀的一種北德語。有一系列用古諾斯語寫成的手稿文字，其中包含一系列從口頭傳統中寫成的[35]首詩[39]。歷史學家似乎對所寫詩歌的具體日期有所猜測，但據估計，這些文字的記錄大約在十三世紀初[40]。儘管流傳故事的口頭傳統早在文字手稿和印刷版本出現之前就存在了。

在現存的文獻中，提到了神話中的神奧丁。學者們講述了創造阿西爾神的神話的故事，其中包括在故事目的論中發現的恆星的想法。帕達里奇·科勒姆（英語：Padaric Colum）寫了一本書，《奧丁的孩子》，其中詳細地重申了阿西爾的眾神如何將名為尤彌爾的巨人帶到他的死亡中，並用他的身體創造了世界，將熾熱的火之國或「固定的星星」的火花附著在天空的圓頂上，這就是尤彌爾的頭骨。[41]。北歐創世神話是將恆星視為固定在地球以外球體上的幾個案例之一。後來的科學文獻表明，直到17世紀，天文思想的這一觀點一直保持在一個版本中。.

西方天文學的發展

[編輯]
尼古拉斯·哥白尼的De revolutionibus orbium coelestium。紐倫堡，1543年；哥白尼作品的列印副本。根據他的宇宙理論，展示了以太陽為中心，外部為「靜止恆星」球體的宇宙模型。

西方天文學知識是基於古希臘哲學和觀測探究的傳統思想。其他文化，包括巴比倫人，也有助於對恆星的思考，他們在西元前18世紀至6世紀建造了星座的地圖。星星的地圖和解釋它們的神話故事的想法，在世界各地和幾種文化中都得到了廣泛的傳播。它們之間的一個相似之處是，人們初步認識到恆星在宇宙中是固定不變的。

這種理解被古希臘人的哲學家，如阿那克西曼德和亞里斯多德，納入了宇宙的理論模型和數學表示中。阿那克西曼德提出了地球上方天體的原始（也是錯誤的）順序：首先是最近的恆星和行星層，然後是月球層，最後是太陽層。 對他來說，「星星」以及太陽和月球都是「充滿火焰的輪狀凝結物」[42]。所有其他後來的行星系統模型都顯示，在宇宙的最外層，即邊緣，有一個包含固定恆星的天球，其餘的移動發光體都位於其中。

柏拉圖、亞里斯多德和其他類似的古代希臘思想家，以及後來的托勒密的宇宙模型顯示了一個以地球為中心的宇宙。托勒密因其《天文學大成》的大量數學著作而具有影響力，該著作試圖解釋恆星運動的特殊性。這些「遊蕩的星星」，即行星，在圍繞宇宙的球體上分佈的恆星背景上移動。這種觀點在中世紀一直存在，後來被後起的天文學家和數學家反駁，如[[尼古拉斯·哥白尼]和約翰尼斯·克卜勒，他們挑戰了長期以來的地心論觀點，構建了一個以太陽為中心的宇宙，這被稱為日心說系統。出現在宇宙所有這些系統中的思想傳統，即使它們的機制不同，但都存在著恆星球體。

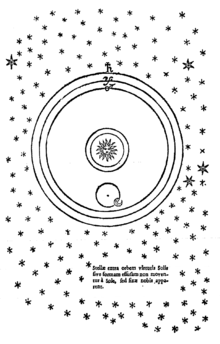
《新哲學世界》中的日心宇宙（關於我們地下世界的新哲學），歸因於威廉·吉爾伯特（英語：William Gilbert (physicist)），1631年（死後）。文中寫道：「太陽能量之球外的恆星，或以滲出物的形式，不會被太陽移動，但對我們來說似乎是固定的。」

十六世紀，許多受哥白尼啟發的作家，如托馬斯·迪格斯[43]、焦爾達諾·布魯諾[44]、和威廉·吉爾伯特[37]主張一個無限延伸甚至無限的宇宙，其它恆星作為遙遠的太陽，為反對亞里斯多德的恆星球體鋪平了道路。

隨著望遠鏡的發明，對天空的研究發生了革命性的變化。1608年首次開發，伽利略聽說後就自己製作了一架望遠鏡[10]。他立刻注意到，行星實際上並不是完全光滑的，而這是亞里斯多德以前提出的理論[10]。他繼續研究天空和星座，很快就知道被研究和繪製的「恆星」只是肉眼無法觸及的巨大宇宙的一小部分[10]。1610年，當他將望遠鏡對準銀河系的微弱條紋時，他發現它分解成無數白色的星形斑點，本身可能是更遠的恆星[45]。

1687年，艾薩克·牛頓發表在他的著作《自然哲學數學原理》中的牛頓定律，在理論家中引發了關於天空機制的進一步問題：牛頓的萬有引力定律表明，恆星不能簡單地固定或靜止，因為它們的引力會導致「相互吸引」，從而使它們相對於彼此移動[5]。

1704年，「太陽系」這個術語進入英語，當時約翰·洛克用它來指出太陽、行星和彗星是一個整體[46]。到那時，人們已經毫無疑問地確定行星是其它世界，恆星是其它遙遠的太陽，所以整個太陽系實際上只是一個巨大宇宙的一小部分，而且絕對是不同的東西。

「固定的星星」沒有被固定

[編輯]
恆星視差效應的原理，以及將一個秒差距定義為距離單位（圖未按比例）。
從太陽系（圖未按比例）看到的遙遠運動天體的自行和速度分量之間的關係。
都卜勒紅移和藍移。

天文學家和自然哲學家之前將天空中的光分為兩組。一組包含「固定的星星」，它們出現上升和下降，但隨著時間的推移保持相同的相對排列，並且沒有明顯的恆星視差，這是由地球軌道運動引起的視位置變化。另一組包含裸眼行星，他們稱之為「流浪恆星」。（太陽和月亮有時也被稱為恆星和行星。）行星似乎在前進和後退，在短時間內（幾週或幾個月）改變它們的位置。它們似乎總是在西方人稱之為黃道帶的恆星帶內移動。行星也可以與恆星區分開來，因為恆星往往會閃爍，而行星似乎會發出穩定的光線。

然而，恆星顯示出視差。它可以用來計算到附近恆星的距離。這種運動只是表面上的；是地球在動。這種效應很小，直到19世紀才被精確量測，但從1670年左右開始，讓·皮卡爾（英語：Jean Picard）、羅伯特·虎克、約翰·佛蘭斯蒂德等天文學家開始探測恆星的運動並嘗試量測。這些運動相當大，如果幾乎難以察覺地小，分數[10]。1832年至1833年，托馬斯·亨德森（英語：Thomas Henderson (astronomer)）在南非開普敦進行了第一次成功的恆星視差量測，在那裡他量測了最近的恆星之一半人馬座α的視差[47]。

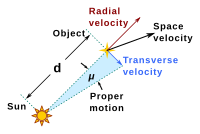
然而，恆星也表現出真正的運動。這種運動可以被視為具有組成部分，這些組成部分包括恆星所屬星系的運動、該星系的旋轉以及恆星在其星系內特有的運動。在星系或星團的情況下，各個組件甚至以非線性管道相互移動。

相對於太陽系，恆星的這種真實運動分為「徑向」運動和「自行」，其中「自行」是視線中的分量[48]。1718年，愛德蒙·哈雷宣佈他發現恆星實際上有自行[49]。古代文化沒有注意到自行，是因為它需要長時間的精確量測才能注意到。事實上，今天的夜空看起來和幾千年前一樣，以至於一些現代星座最初是由巴比倫命名的。

確定自行的一種典型方法是量測恆星相對於一組有限的、選定的非常遙遠物體的位置，這些物體沒有相互運動，並且由於它們的距離，被認為只具有非常小的自行[50]。另一種方法是將恆星在不同時間的照片與更遙遠物體的大背景進行比較[51]。已知具有最大自行的恆星是巴納德星[49]。

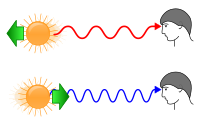
恆星和其它深空天體的徑向速度可以通過光譜學的都卜勒-菲索效應，與靜止物體發出的光相比來揭示，後退的天體（紅移）接收光的頻率會降低，而接近的天體（[藍移]]）的接收光頻率會增加。 威廉·哈金斯在1868年基於觀察到的恆星光譜的紅移，冒險（投機）的估計了天狼星相對於太陽的徑向速度[52]。

「固定的星星」一詞在技術上是不正確的，但儘管如此，它還是被用於歷史背景和經典力學中。當用作觀測的視覺參考時，它們通常被稱為「背景星」或簡稱為「遙遠的星星」，且仍然保留了它們在某種實際意義上被 「固定」 的直觀含義。

在經典力學中

[編輯]
主條目：慣性參考系

在牛頓的時代，恆星被認為是相對於絕對時空靜止的參考系。在其它參考系中，無論是相對於恆星靜止還是相對於恆星勻速平移，牛頓運動定律都應該成立。相較之下，在相對於恆星加速的坐標系中，特別是相對於恆星旋轉的坐標系，運動定律並不以最簡單的形式成立，而必須通過添加慣性力來補充，例如科里奧利力和離心力。

正如我們現在所知，恆星並不是「固定的」。慣性參考系的概念不再與固定恆星或絕對時空聯繫在一起。相對的，慣性系的識別是基於該系中物理定律的簡單性，特別是不存在虛擬力。

慣性定律適用於伽利略坐標系，這是一個假設的系統，相對於該系統，恆星保持固定。

關係力學

[編輯]
「本節參考文獻：[53][54][55][56][57][58][59]」

固定的星星可以在經典力學和關係力學的視野之外觀察到。關係性量子力學是一種場論，是經典力學的一部分，它只規定了粒子之間距離的演變，而不是它們的運動。這一場論的形成為萊布尼茲和馬赫對牛頓力學的責備提供了解決方案。牛頓依賴於絕對時空，而關係力學則不然。用關係力學來描述恆星是符合牛頓運動定律的。

使用特權坐標系（牛頓坐標系）可以觀測行星運動的克卜勒軌道；然而，對個體進化的觀察在關係力學中沒有價值。通過改變個體進化的位置和速度被認為不可觀察的框架，個體進化可能會被扭曲。關係力學中的可觀測值是粒子之間的距離和連接粒子的直線的角度。關係方程處理觀測變數的演化，因為它們與框架無關，可以計算出個別演化可以從不同框架描述的距離的給定演化。這只能意味著規範對稱性採用了萊布尼茨所聲稱的具有基本關係特徵的力學。

萊布尼茨和馬赫責難了使用絕對時空來驗證牛頓框架。萊布尼茨相信物理的關係，而不是相對於形上學定義的框架的個體進化。馬赫會責難牛頓的絕對加速度概念，指出水的形狀只能證明相對於宇宙其他部分的旋轉。馬赫的責難後來被阿爾伯特·愛因斯坦接受，他提出了「馬赫原理」，即慣性是由與宇宙其他部分的相互作用決定的。關係力學可以被稱為馬赫理論。

20世紀力學的改革已經成熟，相關原理也已成熟。力學定律結合了勢能和動力學變數，在這種情況下，勢能已經是相關的，因為它包含了粒子之間的距離。 牛頓動能包含個別速度，試圖將其重新表述為相對速度和距離的可能性。然而，這些嘗試導致了許多與慣性相反的概念，這些概念沒有得到支持，許多人同意牛頓動能的基本前提應該得到保留。

粒子之間距離的演變不需要慣性系來顯示自己，而是將其用作粒子的座標。這兩個不同的力學定律在概念上是不同的。一個例子是子系統的隔離，牛頓定律將根據絕對、初始和最終條件描述其演化。關係力學將根據內部和外部距離來描述其演化，因此即使系統是「孤立的」，其演化也將始終由子系統與宇宙其他部分的關係來描述。

文學參考資料

[編輯]
  • 但丁在他的神曲最後一章節「樂園」中，將固定的星星作為十層天中的第八層。

相關條目

[編輯]

參考資料

[編輯]
  1. ^ 1.0 1.1 1.2 1.3 Pedersen, Olaf. Early physics and astronomy : a historical introduction. Pihl, Mogens. London: MacDonald and Janes. 1974: 59–63. ISBN 0-356-04122-0. OCLC 1094297. 
  2. ^ Cornford, Fracis. Plato's Cosmology; the Timaeus of Plato, Translated with a Running Commentary by Francis Macdonald Cornford. Indianapolis: Bobbs-Merrill. 1960: 54–57. 
  3. ^ Pedersen, Olaf. Early physics and astronomy : a historical introduction. Pihl, Mogens. London: MacDonald and Janes. 1974: 65–67. ISBN 0-356-04122-0. OCLC 1094297. 
  4. ^ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 Lang, Kenneth R. A companion to astronomy and astrophysics : chronology and glossary with data tables. [New York]. ISBN 0-387-30734-6. OCLC 70587818. 
  5. ^ 5.0 5.1 5.2 5.3 5.4 5.5 Bartusiak, Marcia. Archives of the universe : a treasury of astronomy's historic works of discovery需要免費註冊 1st. New York: Pantheon Books. 2004. ISBN 0-375-42170-X. OCLC 54966424. 
  6. ^ Case, Stephen. Divine Animals: Plato, Aristotle, and the Stars. Mercury. Summer 2013, 42: 29–31 –透過Academia. 
  7. ^ VII. The Heavens, Aristotle, Columbia University Press: 145–162, 1960-12-31, ISBN 978-0-231-87855-5, doi:10.7312/rand90400-008 
  8. ^ Heath, Thomas. The Copernicus of Antiquity (Aristarchus of Samos). London: The Macmillan Company. 1920: 41. 
  9. ^ 9.0 9.1 Pedersen, Olaf. Early physics and astronomy : a historical introduction. Pihl, Mogens. London: MacDonald and Janes. 1974: 63–64. ISBN 0-356-04122-0. OCLC 1094297. 
  10. ^ 10.0 10.1 10.2 10.3 10.4 10.5 10.6 10.7 Taton, René; Wilson, Curtis. Planetary astronomy from the Renaissance to the rise of astrophysics. Cambridge University Press. 1989. ISBN 0-521-24254-1. OCLC 769917781. 
  11. ^ 11.0 11.1 Carrol, Bradley and Ostlie, Dale, An Introduction to Modern Astrophysics, Second Edition, Addison-Wesley, San Francisco, 2007. pp. 4
  12. ^ Bruce S. Eastwood, Ordering the Heavens: Roman Astronomy and Cosmology in the Carolingian Renaissance (Leiden: Brill, 2007), pp. 238-9.
  13. ^ Margaret Deanesly, A History of Early Medieval Europe: From 476–911 (New York: Routledge, 2020).
  14. ^ "The most elucidating approach to Martianus is through his fortuna (Stahl 1965, p. 105).
  15. ^ 15.0 15.1 Pedersen, Olaf. Early physics and astronomy : a historical introduction. Pihl, Mogens. London: MacDonald and Janes. 1974: 303–307. ISBN 0-356-04122-0. OCLC 1094297. 
  16. ^ 16.0 16.1 16.2 Christianson, J. R. (John Robert). On Tycho's island : Tycho Brahe and his assistants, 1570-1601. Cambridge, U.K.: Cambridge University Press. 2000: 122-123. ISBN 0-521-65081-X. OCLC 41419611. 
  17. ^ Goldstein, Bernard; Hon, Giora. Kepler's Move from Orbs to Orbits: Documenting a Revolutionary Scientific Concept. Perspectives on Science. 2005, 13: 74–111. S2CID 57559843. doi:10.1162/1063614053714126. 
  18. ^ Moore, Patrick. The A-Z of astronomy需要免費註冊 Rev. New York: Scribner. 1976. ISBN 0-684-14924-9. OCLC 2967962. 
  19. ^ Hesiod, Theogony 517–520
  20. ^ Most of Anaximander's model of the Universe comes from pseudo-Plutarch (II, 20–28):
    "[The Sun] is a circle twenty-eight times as big as the Earth, with the outline similar to that of a fire-filled chariot wheel, on which appears a mouth in certain places and through which it exposes its fire, as through the hole on a flute. [...] the Sun is equal to the Earth, but the circle on which it breathes and on which it's borne is twenty-seven times as big as the whole earth. [...] [The eclipse] is when the mouth from which comes the fire heat is closed. [...] [The Moon] is a circle nineteen times as big as the whole earth, all filled with fire, like that of the Sun".
  21. ^ Thurston, Hugh. Early astronomy. New York: Springer-Verlag New York. 1994: 111. ISBN 0-387-94107-X. 
  22. ^ Sider, D. Anaxagoras on the Size of the Sun. Classical Philology. 1973, 68 (2): 128–129. JSTOR 269068. S2CID 161940013. doi:10.1086/365951. 
  23. ^ Curd, Patricia. Anaxagoras. 扎爾塔, 愛德華·N (編). 《史丹佛哲学百科全书》. 2019. 
  24. ^ Yavetz, Ido. On the Homocentric Spheres of Eudoxus. Archive for History of Exact Sciences. February 1998, 52 (3): 222–225. Bibcode:1998AHES...52..222Y. JSTOR 41134047. S2CID 121186044. doi:10.1007/s004070050017. 
  25. ^ Pedersen, Olaf. Early physics and astronomy. A historical introduction. Cambridge (UK): Cambridge University Press. 1993. ISBN 0-521-40340-5. 
  26. ^ Thurston, Hugh. Early astronomy. New York: Springer-Verlag New York. 1994: 118. ISBN 0-387-94107-X. 
  27. ^ Heath (1920，第302]頁)
  28. ^ Hirshfeld, Alan W. The Triangles of Aristarchus. The Mathematics Teacher. 2004, 97 (4): 228–231. ISSN 0025-5769. JSTOR 20871578. doi:10.5951/MT.97.4.0228. 
  29. ^ Archimedes, The Sand Reckoner 511 R U, by Ilan Vardi, accessed 28-II-2007.
  30. ^ Arenarius, I., 4–7
  31. ^ Russo, Lucio. The forgotten revolution : how science was born in 300 BC and why it had to be reborn. Berlin: Springer. 2004: 68. ISBN 3-540-20396-6. OCLC 52945835. 
  32. ^ G. J. Toomer, "Hipparchus on the distances of the sun and moon," Archive for History of Exact Sciences 14 (1974), 126–142.
  33. ^ North, John. The Norton History of Astronomy and Cosmology. New York: W.W.Norton & Company, Inc. 1995: 115. ISBN 0-393-03656-1. 
  34. ^ Lindberg, David C. The Beginnings of Western Science. Chicago: University of Chicago Press. 1992: 251. ISBN 978-0-226-48231-6. 
  35. ^ Van Helden, Albert. Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley. Chicago and London: University of Chicago Press. 1985: 28–40. ISBN 978-0-226-84882-2. 
  36. ^ Almagest – Ptolemy (Elizabeth). projects.iq.harvard.edu. [2022-11-05] （英語）. 
  37. ^ 37.0 37.1 Gilbert, William. Book 6, Chapter III. De Magnete. 由Mottelay, P. Fleury翻譯. (Facsimile). New York: Dover Publications. 1893. ISBN 0-486-26761-X. 
  38. ^ Kennedy, E. S. The Astronomy of Levi ben Gerson (1288–1344): A Critical Edition of Chapters 1–20 with Translation and Commentary. Levi ben Gerson, Bernard R. Goldstein. Isis. 1986-06-01, 77 (2): 371–372. ISSN 0021-1753. doi:10.1086/354184. 
  39. ^ Bray, Oliver. The Elder or Poetic Edda; commonly known as Saemund's Edda. Edited and translated with introd. and notes by Oliver Bray. Illustrated by W.G. Collingwood 1. archive.org: London Printed for the Viking Club. 1908. 
  40. ^ Lindow, John. Norse Mythology: A Guide to Gods, Heroes, Rituals, and Beliefs. books.google.com: Oxford University Press. 2001. ISBN 9780199839698. 
  41. ^ Colum, Padaric. The Children of Odin: The Book of Northern Myths. Guternberg Project: Gutenberg Project eBook. March 2, 2008: 62–69. 
  42. ^ Khan, Charles. Anaximander and the Origins of Greek Cosmology. New York: Columbia University Press. 1960: 84–85. ISBN 9780231903349. 
  43. ^ Hellyer, Marcus (編). The Scientific Revolution: The Essential Readings. Blackwell Essential Readings in History 7. John Wiley & Sons. 2008: 63. ISBN 9780470754771. The Puritan Thomas Digges (1546–1595?) was the earliest Englishman to offer a defense of the Copernican theory. ... Accompanying Digges's account is a diagram of the universe portraying the heliocentric system surrounded by the orb of fixed stars, described by Digges as infinitely extended in all dimensions. 
  44. ^ Bruno, Giordano. Third Dialogue. On the infinite universe and worlds. （原始內容存檔於27 April 2012）.  已忽略未知參數|df= (幫助)
  45. ^ Galileo Galilei, Sidereus Nuncius (Venice, (Italy): Thomas Baglioni, 1610), pages 15 and 16. 網際網路檔案館的存檔，存檔日期March 16, 2016，.
    English translation: Galileo Galilei with Edward Stafford Carlos, trans., The Sidereal Messenger (London: Rivingtons, 1880), pages 42 and 43. 網際網路檔案館的存檔，存檔日期December 2, 2012，.
  46. ^ solar (adj.). Online Etymology Dictionary. [2 May 2022]. （原始內容存檔於18 March 2022）. 
  47. ^ Henderson, Thomas. On the Parallax of α Centauri. Monthly Notices of the Royal Astronomical Society. 1839, 4 (19): 168–170. Bibcode:1839MNRAS...4..168H. doi:10.1093/mnras/4.19.168 可免費查閱. 
  48. ^ John R. Percy. Understanding Variable Stars. Cambridge University Press. 2007: 21. ISBN 978-0-521-23253-1. 
  49. ^ 49.0 49.1 Theo Koupelis; Karl F. Kuhn. In Quest of the Universe需要免費註冊. Jones & Bartlett Publishers. 2007: 369. ISBN 978-0-7637-4387-1. 
  50. ^ Peter Schneider. Extragalactic Astronomy and Cosmology. Springer. 2006: 84, §2.6.5. ISBN 3-540-33174-3. 
  51. ^ Christopher De Pree; Alan Axelrod. The Complete Idiot's Guide to Astronomy需要免費註冊 3rd. Alpha Books. 2004: 198. ISBN 1-59257-219-7. 
  52. ^ Huggins, W. Further observations on the spectra of some of the stars and nebulae, with an attempt to determine therefrom whether these bodies are moving towards or from the Earth, also observations on the spectra of the Sun and of Comet II. Philosophical Transactions of the Royal Society of London. 1868, 158: 529–564. Bibcode:1868RSPT..158..529H. doi:10.1098/rstl.1868.0022. 
  53. ^ Ferraro, Rafael. The Frame of Fixed Stars in Relational Mechanics. Foundations of Physics. 2017, 47 (1): 71. Bibcode:2017FoPh...47...71F. S2CID 254514108. arXiv:1801.00676 可免費查閱. doi:10.1007/s10701-016-0042-7. 
  54. ^ Gottfried Wilhelm von Leibniz; Samuel Clarke; Gottfried Wilhelm Freiherr von Leibniz; Robert Gavin Alexander. The Leibniz-Clarke correspondence: Together with extracts from Newton's Principia and Opticks. Manchester University Press. 1956. ISBN 978-0-7190-0669-2. 
  55. ^ Mach, Ernst; McCormack, Translated by Thomas J. The Science of Mechanics. 2013. Bibcode:2013scme.book.....M. 
  56. ^ Einstein, Albert. Gibt es eine Gravitationswirkung, die der elektrodynamischen Induktionswirkung analog ist?. Vierteljahrschrift FÜR Gerichtliche Medizin und ÖFfentliches SanitÄTswesen. 1912, 44: 37. Bibcode:1912VMed...44...37E. 
  57. ^ Einstein, A. Die formale Grundlage der allgemeinen Relativitätstheorie. Albert Einstein: Akademie-Vorträge. 2005: 8–64. ISBN 9783527406098. doi:10.1002/3527608958.ch2. 
  58. ^ Einstein, A. Die Grundlage der allgemeinen Relativitätstheorie. Annalen der Physik. 1916, 354 (7): 769. Bibcode:1916AnP...354..769E. doi:10.1002/andp.19163540702. 
  59. ^ Einstein, A. Prinzipielles zur allgemeinen Relativitätstheorie. Annalen der Physik. 1918, 360 (4): 241. Bibcode:1918AnP...360..241E. doi:10.1002/andp.19183600402. 


取自「https://zh.wikipedia.org/w/index.php?title=固定的星星&oldid=84513410」