能帶結構
| 建議將此條目或章節併入能帶理論。(討論) |
在固態物理學中,固體的能帶結構 (又稱電子能帶結構)描述了禁止或允許電子所帶有的能量,這是周期性晶格中的量子動力學電子波衍射引起的。材料的能帶結構決定了多種特性,特別是它的電學、光學和熱學性質。
為何有能帶[編輯]
單獨原子的電子占據了原子軌道,形成一個分立的能級結構。如果幾個原子集合成分子,他們的原子軌道發生類似於耦合振盪的分離。這會產生與原子數目成比例的分子軌道。當數目非常巨大(數量級為或更多)的原子集合成固體時,軌道數目急劇增多,軌道相互間的能量的差別將會變的非常小。雖然,無論多少原子聚集在一起,軌道能量的分布都是不連續的,但因為固體中的能級如此之多,所以一群相鄰的能級,可以被視為一個連續能譜,也就是一個能帶。而能帶與能帶之間的間隙,則為能隙。
物理學中流行的方法是從不帶電的電子和原子核出發,因為它們是自由的平面波,可以具有任意能量,並在帶電後衰減。這導致了布拉格反射和能帶結構。
基本概念[編輯]
晶體結構的對稱性與波向量[編輯]
晶體能帶結構的計算需要利用晶格的周期性和對稱性 ,通常會假設晶體是理想的 ,並具有周期邊界和離散的平移對稱性。單電子薛丁格方程在晶體的周期性勢壘中的解即為布洛赫波,如下所示:
- ,
其中k稱為波向量。對於每一個k,薛丁格方程都有多個解,解的數量用n表示,也就是能帶的條數。每條能帶都隨著k周期性變化,我們用En(k)來表示。對於包含原子數非常巨大的真實晶體,可以當成趨於熱力學極限並恢復平移對稱性,並用布洛赫波近似地描述晶體的體態波函數性質。
由於晶體結構的離散平移對稱性,能帶圖通常只畫第一布里淵區以內的k。第一布里淵區之外的波向量對應的解和之內的解是對應的。
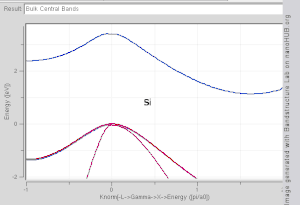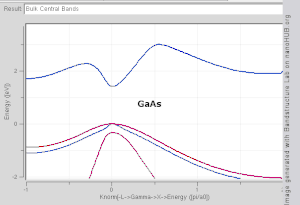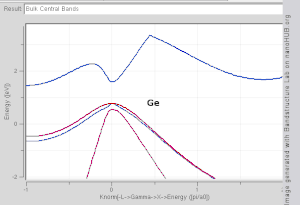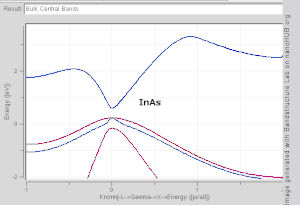
由於布里淵區中高對稱點一般會伴隨能級簡併 ,並反應晶格對稱性,所以通常會沿著高對稱點來展示能帶結構圖。 布里淵區中的高對稱點常常被記為Γ, Δ, Λ, Σ。此處展示幾種常見半導體的能帶結構圖如右圖所示。
不同固體的能帶結構[編輯]

固體材料的能帶結構由多條能帶組成,能帶分為導帶、價帶和禁帶等,導帶和價帶間的空隙稱為禁帶(能隙)(即右邊第二副圖中所示的)。
能帶結構可以解釋固體中導體、半導體、絕緣體三大類區別的由來。材料的導電性是由「傳導帶」中含有的電子數量決定。當電子從「價帶」獲得能量而跳躍至「傳導帶」時,電子就可以在帶間任意移動而導電。
一般常見的金屬導體,因為其傳導帶與價帶之間的「能隙」非常小,在室溫下電子很容易獲得能量而跳躍至傳導帶而導電,而絕緣材料(絕緣體)則因為能隙很大(通常大於9電子伏特),電子很難跳躍至傳導帶,所以無法導電。一般半導體材料的能隙約為1至3電子伏特,介於導體和絕緣體之間。因此只要給予適當條件的能量激發,或是改變其能隙之間距,此材料就能導電。
導帶的最低點和價帶的最高點處於同一k位置的稱為直接帶隙半導體。比如GaAs和InAs。 導帶的最低點和價帶的最高點處於不同k位置的稱為間接帶隙半導體。比如Si和Ge。他們的能帶結構圖如右上第一幅圖所示。
態密度[編輯]
態密度函數g(E)是指電子在能量E處單位體積單位能量的電子態數量。
態密度函數對於在能帶理論基礎上相關的計算非常重要。例如,g(E)乘以費米-狄拉克分布即可以得到電子濃度與能量的關係式。
在能帶間隙中,態密度g(E)=0。而在范霍夫奇點(Van Hove singularity),態密度會是發散的。
能帶填充[編輯]
在熱力學平衡狀態下,能量E充滿電子的可能性由費米-狄拉克(Fermi-Dirac)分布給出,該熱力學分布考慮了泡利不相容原理。 儘管有無限多個能帶,因此有無限多個狀態,但是在這些能帶中只有有限數量的電子。電子數的優選值是靜電的結果:即使材料的表面可以帶電,材料的內部體積也傾向於是電荷中性的。電荷中性的條件意味著N / V必須與材料中質子的密度匹配。為此,材料會進行靜電自我調節,使能帶結構上下移動能量(從而移動g(E)),直到相對於費米能級達到正確的平衡。
費米能級附近的能帶名稱(導帶,價帶) 固體具有無限數量的允許帶,就像原子具有無限多個能級一樣。但是,大多數能帶的能量太高,通常在通常情況下會被忽略。[1]相反,與核心軌道相關的能帶非常低(例如1s電子)。這些低能芯帶通常也被忽略,因為它們始終保持充滿電子,因此是惰性的。[2]同樣,材料在其整個能帶結構中都具有多個帶隙。
與電子和光電相關的最重要的帶和帶隙是那些能量接近費米能級的帶。根據材料,費米能級附近的帶和帶隙被賦予特殊名稱:
在半導體或帶絕緣子中,費米能級被帶隙所圍繞,稱為帶隙(以將其與帶結構中的其他帶隙區分開)。帶隙以上的最接近的帶稱為導帶,帶隙下方的最接近的帶稱為價帶。 「價帶」之類的名稱類似於化學,因為在半導體(和絕緣體)中,價帶是由價軌道構成的。 在金屬或半金屬中,費米能級在一個或多個允許帶的內部。在半金屬中,該帶通常被稱為「導帶」或「價帶」,這取決於電荷傳輸是更類似於電子的還是類似於空穴的,類似於半導體。然而,在許多金屬中,這些帶既不像電子一樣也不像空穴一樣,通常是由價態軌道組成的,因此通常被稱為「價帶」。[3] 金屬的能帶結構中的能隙對低能物理並不重要,因為它們與費米能級相距太遠。
晶體的能帶結構[編輯]
布里淵區[編輯]
晶體能帶結構理論[編輯]
擬設是使用布洛赫波的周期性晶格中電子波的特例,通常在衍射動力學理論中對其進行處理。每個晶體都是可以用Bravais晶格表徵的周期性結構,對於每個Bravais晶格,我們可以確定倒易晶格,該倒易晶格將周期性封裝在三個倒易晶格矢量(b1,b2,b3)的集合中。現在,可以將與直接晶格共享相同周期性的任何周期性電勢V(r)展開為傅立葉級數,該傅立葉級數的唯一不消失的成分是與倒易晶格矢量相關的成分。
近自由電子近似[編輯]
在近自由電子的近似中,電子之間的相互作用被完全忽略。這種近似允許使用布洛赫定理,布洛赫定理指出周期性電勢中的電子具有波函數和能量,這些波函數和能量在波矢量中具有周期性,直到相鄰倒易晶格矢量之間的相移恆定為止。 近自由電子近似模型在金屬(如相鄰原子之間的距離很小)的材料計算中效果特別好。在這種材料中,原子軌道和相鄰原子上的電勢的重疊相對較大。在那種情況下,電子的波函數可以通過(修正的)平面波來近似。像鋁這樣的金屬的能帶結構甚至接近於空晶格近似。
緊束縛模型[編輯]
與近自由電子近似相反的極端假設晶體中的電子的行為非常像組成原子的集合。這個緊束縛模型假定獨立的單電子Schrödinger方程的解可以通過原子軌道的線性組合很好地近似. 緊束縛模型的近似在原子軌道與相鄰原子上的電勢重疊有限的材料中效果很好。緊束縛模型-哈密頓主義者基於原子sp3軌道很好地描述了諸如Si,GaAs,SiO2和金剛石之類的材料的能帶結構。在過渡金屬中,混合的緊束縛-近自由電子近似模型用於描述寬的近自由電子近似導帶和窄的嵌入式緊束縛 d帶。 Wannier函數的原子軌道部分的徑向函數最容易通過使用偽電勢方法來計算。 近自由電子近似模型,緊束縛模型或組合的近自由電子近似-緊束縛模型頻帶結構計算[4]有時使用基於偽勢方法的波動函數近似擴展,通常被用作進行進一步計算的起點。
KKR模型[編輯]
Korringa-Kohn-Rostoker(KKR)方法最初是由Korringa在1947年開發的,他使用多重散射理論來求解Schrödinger方程並確定周期性固體的能帶結構。七年後,Kohn和Rostoker 提出了一種與Korringa等效的方法,但使用了格林函時稱之為Korringa-Kohn-Rostoker(KKR)方法。[5][6] KKR方法最重要的特徵可能是,從非相對論描述轉向相對論描述時,其形式結構不會改變。KKR 或格林函數公式最重要的特徵是(1)它將問題的兩個方面分開:結構(原子的位置)與散射(原子的化學特性); (2)格林函數提供了一種對電子特性進行局部描述的自然方法,可以適用於合金和其他無序系統。自四十年代後期以來,KKR方法已經進行了幾處改進。這些改進之一是所謂的遮蔽(screened or tight binding)的Korringa-Kohn-Rostoker(sKKR)方法。 sKKR方法允許在多重散射理論的框架內以二維方式計算表面,界面以及通常具有二維周期性的一般分層系統的電子特性,而無需任何進一步的近似。這種近似的最簡單形式是將非重疊球(稱為鬆餅罐)置於原子位置上。在這些區域內,電子所經歷的電勢近似於關於給定的原子核是球對稱的。在剩餘的間隙區域中,屏蔽電位近似為常數。強制以原子為中心的球體和間隙區域之間的電勢連續性。利用這種格林函數和Korringa–Kohn–Rostoker方法,可以獲得Korringa–Kohn–Rostoker相干勢近似(KKR-CPA)。 KKR-CPA用於計算替代固溶合金的電子態,而Bloch定理不成立。可以使用局部自洽多重散射(LSMS)方法找到更廣泛範圍的凝聚態結構的電子態,該方法也基於單粒子格林函數。
密度泛函理論[編輯]
在最近的物理學文獻中,大多數電子結構和能帶圖都是使用密度泛函理論(DFT)計算的,密度泛函理論不是模型而是一種理論,即凝聚態物理的微觀第一原理理論,通過在電子密度的函數中引入交換相關項來解決電子-電子多體問題。在許多情況下,例如通過角度分辨光發射光譜法(ARPES),發現DFT計算的譜帶與實驗測量的譜帶一致。特別地,帶形通常通過DFT很好地再現。但是,與實驗結果相比,DFT譜帶也存在系統誤差。尤其是,DFT似乎系統地低估了絕緣體和半導體中的帶隙約30-40%。[7]
通常認為,DFT是僅預測系統基態性質(例如,總能量,原子結構等)的理論,並且激發態性質不能由DFT確定。這是一個誤解。原則上,DFT可以確定給定將基態密度映射到該特性的功能的系統的任何特性(基態或激發態)。這是Hohenberg–Kohn定理的本質。[8] 然而,在實踐中,不存在將基態密度映射到材料內電子的激發能的已知功能。因此,在文獻中被稱為DFT能帶圖的是DFT Kohn-Sham能量的表示,即虛構的非相互作用系統Kohn-Sham系統的能量,根本沒有物理解釋。不可將Kohn-Sham電子結構與系統的真實准粒子電子結構相混淆,而且對於Hartree-Fock能量也沒有Koopman定理對Kohn-Sham能量的持有,可以將其真正視為準粒子能量的近似值。因此,從原理上講,基於Kohn-Sham的DFT並不是能帶理論,即不是適合於計算能帶和能帶曲線的理論。原則上,基於時間的DFT可用於計算真實的能帶結構,儘管在實踐中這通常很困難。一種流行的方法是使用混合功能,其中包含Hartree-Fock精確交換的一部分。這大大改善了半導體的預測帶隙,但對金屬和寬帶隙材料的可靠性較差。[9]
格林函數方法和從頭算起GW近似[編輯]
為了計算包括電子-電子相互作用多體效應的能帶,人們可以訴諸所謂的格林函數方法。確實,對系統格林函數功能的了解不僅提供了基態(總能量),而且還提供了系統的激發態可觀測值。格林函數的極點是准粒子能量,即固體的能帶。一旦知道系統的自能量,就可以通過求解戴森方程來計算格林函數。對於像固體這樣的真實系統,自能量是一個非常複雜的量,通常需要近似值來解決該問題。一種這樣的近似是GW近似,從數學形式上稱自能量為格林函數G與動態篩選的相互作用W的乘積Σ= GW。這種方法在解決能帶圖的計算時更相關(以及超出範圍的數量(例如光譜函數),並且也可以完全從頭算起。 GW近似值似乎提供了與實驗一致的絕緣體和半導體的帶隙,從而糾正了系統性DFT低估。
動力學平均場理論[編輯]
Mott絕緣體是指在金屬中,儘管還有空的能階,但是電子間的相互作用太強,導致其它的電子沒有辦法在空的能階中移動。所以儘管看起來跟金屬一樣,但是導電性質卻像絕緣體。儘管近乎自由的電子近似能夠描述電子能帶結構的許多特性,但該理論的一個結果是,它預測了每個晶胞中相同數量的電子。如果電子數是奇數,則我們可以預期每個晶胞中都有一個不成對的電子,因此價帶未被完全占據,從而使該材料成為導體。但是,每單位晶格中具有奇數個電子的材料(例如CoO)是絕緣體,與該結果直接衝突。這種材料被稱為Mott絕緣體,並且需要包含詳細的電子-電子相互作用(在能帶理論中僅作為對晶體電勢的平均影響來處理)以解釋差異。哈伯德模型是一個可以包含這些相互作用的近似理論。可以在所謂的動力學平均場理論中以非擾動的方式對待它,該理論試圖彌合幾乎自由電子近似與原子極限之間的差距。然而,在形式上,狀態在這種情況下不是不相互作用的,並且帶結構的概念不足以描述這些情況。
其它[編輯]
計算能帶結構是理論固態物理學中的重要課題。除上述模型外,其他模型還包括:
- 空晶格近似:已劃分為晶格的自由空間區域的「帶結構」。
- k·p擾動理論是一種僅用幾個參數就可以大致描述能帶結構的技術。該技術通常用於半導體,並且模型中的參數通常是通過實驗確定的。
- Kronig-Penney模型,一維矩形井模型,用於說明帶形成。它雖然簡單,但可以預測許多重要現象,但不是定量的。
- 哈伯德模型:
能帶結構已被普遍化為複數的波矢量,從而產生了所謂的復能帶結構,可決定了材料的許多周期性被破壞的特性,例如在表面、界面和缺陷處,都令人關注。
每個模型都很好地描述了某些類型的固體,而其他模型則描述得很差。幾乎自由的電子模型對金屬有效,但對非金屬則較差。緊束縛模型對於離子絕緣(例如金屬鹵化物鹽(例如NaCl))非常精確。
參考資料[編輯]
- ^ High-energy bands are important for electron diffraction physics, where the electrons can be injected into a material at high energies, see Stern, R.; Perry, J.; Boudreaux, D. Low-Energy Electron-Diffraction Dispersion Surfaces and Band Structure in Three-Dimensional Mixed Laue and Bragg Reflections. Reviews of Modern Physics. 1969, 41 (2): 275. Bibcode:1969RvMP...41..275S. doi:10.1103/RevModPhys.41.275..
- ^ Low-energy bands are however important in the Auger effect.
- ^ In copper, for example, the effective mass is a tensor and also changes sign depending on the wave vector, as can be seen in the de Haas–van Alphen effect; see https://www.phys.ufl.edu/fermisurface/ (頁面存檔備份,存於網際網路檔案館)
- ^ Walter Ashley Harrison. Electronic Structure and the Properties of Solids. Dover Publications. 1989. ISBN 978-0-486-66021-9.
- ^ Joginder Singh Galsin. Impurity Scattering in Metal Alloys. Springer. 2001. Appendix C. ISBN 978-0-306-46574-1.
- ^ Kuon Inoue, Kazuo Ohtaka. Photonic Crystals. Springer. 2004: 66. ISBN 978-3-540-20559-3.
- ^ Theoretical study on copper’s energetics and magnetism in TiO2 polymorphs (頁面存檔備份,存於網際網路檔案館) Journal of Applied Physics, 2013,113(23), 233913
- ^ Hohenberg, P; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. Nov 1964, 136 (3B): B864–B871. Bibcode:1964PhRv..136..864H. doi:10.1103/PhysRev.136.B864.
- ^ Paier, J.; Marsman, M.; Hummer, K.; Kresse, G.; Gerber, IC.; Angyán, JG. Screened hybrid density functionals applied to solids.. J Chem Phys. Apr 2006, 124 (15): 154709. Bibcode:2006JChPh.124o4709P. PMID 16674253. doi:10.1063/1.2187006.
參考文獻[編輯]
- Kotai no denshiron (The theory of electrons in solids), by Hiroyuki Shiba, ISBN 4-621-04135-5
- Microelectronics, by Jacob Millman and Arvin Gabriel, ISBN 0-07-463736-3, Tata McGraw-Hill Edition.
- Solid State Physics, by Neil Ashcroft and N. David Mermin, ISBN 0-03-083993-9,
- Introduction to Solid State Physics by Charles Kittel, ISBN 0-471-41526-X
- Electronic and Optoelectronic Properties of Semiconductor Structures - Chapter 2 and 3 by Jasprit Singh, ISBN 0-521-82379-X
參見[編輯]
| |||||||||||||||||||||||||||
| |||||||||||||||||
| ||||||||||||||||||||||||||||||||



