计算解剖学

计算解剖学是一门多领域交叉学科，是关注定量研究与解剖形状可变性建模的生物学领域。其包含了数学、统计学和数据分析方法在建模及生物结构模拟上的发展与应用。

计算解剖学内容丰富，涵盖解剖学、应用数学及纯数学、机器学习、计算力学、计算科学、生物成像、神经科学、物理学、概率论与统计学内容；还与流体力学和几何力学有联系。另外，还包含较新的跨领域学科，如生物信息学和神经信息学，它们的解释用到了来自原传感器成像方式（如磁共振成像）的元数据。其关注待测区域的解剖结构，而非成像设备。这与计算语言学的精神类似。

在计算解剖学中，微分同胚群主要通过坐标变换研究不同坐标系，坐标变换由${\mathbb {R} }^{3}$中流的拉格朗日与欧拉向量生成。不同坐标间的流受测地流约束，后者满足流动能最小作用原理。动能由索伯列夫平滑度范数定义，流速的每个分量都有严格多于2个的广义平方可积导数，保证$\mathbb {R} ^{3}$中的流微分同胚。 这也说明，微分同胚形状动量逐点满足测地线的欧拉-拉格朗日方程，是通过速度场上邻域的空间导数决定的。这与不可压缩流的情形不同，后者的动量是速度的逐点函数。计算解剖学横贯黎曼流形与非线性全局分析，其中微分同胚群是研究的重点。新出现的高维形状理论是计算解剖学许多研究的重点，如形状统计这一新兴领域中出现的问题一样。 计算解剖学的度量结构在精神上与形态测量学有关，区别在于，计算解剖学关注通过微分同胚变换的坐标系的无穷维空间。

计算解剖学的可变形模板轨道模型

人体解剖模型是可变形模板，是群作用下的轨道。可变形模板模型一直是格雷纳德是度量模式理论的核心，通过模板说明典型性，通过模板的变换说明可变性。微分几何中的经典表述是，将群作用下的轨道表示为可变形模板。形状空间可表为$m\in {\mathcal {M}}$，群$({\mathcal {G}},\circ )$具有组合律$\circ$；形状上的群作用表为$g\cdot m$，当中群作用$g\cdot m\in {\mathcal {M}},m\in {\mathcal {M}}$定义为满足

$(g\circ g^{\prime })\cdot m=g\cdot (g^{\prime }\cdot m)\in {\mathcal {M}}.$

模板轨道${\mathcal {M}}$成为所有形状的空间，${\mathcal {M}}\doteq \{m=g\cdot m_{\mathrm {temp} },g\in {\mathcal {G}}\}$，在${\mathcal {G}}$的元素的作用下同质。

图中描绘了杏仁核、内侧皮层与海马体的3个内侧颞叶结构，MRI背景中还嵌入了标靶。

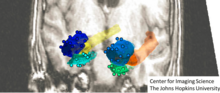
计算解剖学的轨道模型与线性代数相比像是抽象代数，因为群对形状的作用不线性。这是对线性代数经典模型的推广，有限维${\mathbb {R} }^{n}$向量推广为有限维解剖子流形（点、线、面、体）及其图像，线性代数的$n\times n$维矩阵推广为基于线性与仿射变换和更一般的高维微分同胚群的坐标变换。

形状与形式

中心对象是计算解剖学中的形状或形式，如${\mathbb {R} }^{3}$的0、1、2、3维子流形，或由MRI及fMRI等医学成像技术生成的图像。

Figure showing triangualted meshes generated from populations of many segmented MRI brains. Each different surface represents a different shape in shape space.

描绘皮层下杏仁核、海马体、丘脑、尾状核、脑室的三角网格面。形状表示为三角网格$m(u),u\in U\subset {\mathbb {R} }^{1}\rightarrow {\mathbb {R} }^{2}$

0维流形是基准点；1维流形是脑沟回之类的曲线；2维流形对应解剖子结构的边界，如中脑皮质下结构或新皮质回旋面；子体对应于人体的子区域，如心脏、丘脑、肾脏等。

基准点$X\doteq \{x_{1},\dots ,x_{n}\}\subset {\mathbb {R} }^{3}\in {\mathcal {M}}$是无其他结构的点集。 子流形，如面$X\subset {\mathbb {R} }^{3}\in {\mathcal {M}}$是局部表或浸入$m:U\subset {\mathbb {R} }^{1,2}\rightarrow {\mathbb {R} }^{3}$，$m(u),u\in U$参数化建模的点集（见图中显示的网格面形状）。 MRI或DTI图像等$I\in {\mathcal {M}}$，是稠密函数 $I(x),x\in X\subset {\mathbb {R} }^{1,2,3}$是标量、向量与矩阵（见显示标量图的图像）。

群与群作用

3D大脑MRI图像切面，代表基于T1加权的标量图$I(x),x\in {\mathbb {R} }^{2}$。

随着线性代数作为机械工程、电气工程与应用数学中分析信号与系统的基本模型逐渐普及，群和群作用已为工程界所熟悉。线性代数的核心结构是矩阵群（可逆），对n阶方阵A的群作用通常定义为$n\times 1$向量；线性代数中的轨道是$y=A\cdot x\in {\mathbb {R} }^{n}$给出的n个向量之集，其是通过${\mathbb {R} }^{n}$的轨道的矩阵的群作用。

计算解剖学中，定义在${\mathbb {R} }^{3}$的体上的中心群是微分同胚${\mathcal {G}}\doteq Diff$，具有3分量映射$\phi (\cdot )=(\phi _{1}(\cdot ),\phi _{2}(\cdot ),\phi _{3}(\cdot ))$、函数复合律$\phi \circ \phi ^{\prime }(\cdot )\doteq \phi (\phi ^{\prime }(\cdot ))$、逆$\phi \circ \phi ^{-1}(\cdot )=\phi (\phi ^{-1}(\cdot ))=id$。

最常用的是标量图像$I(x),x\in {\mathbb {R} }^{3}$，通过逆作用于右侧。

$\phi \cdot I(x)=I\circ \phi ^{-1}(x),x\in {\mathbb {R} }^{3}$.

对子流形$X\subset {\mathbb {R} }^{3}\in {\mathcal {M}}$，参数化为图或浸入$m(u),u\in U$，微分同胚作用流的位置

$\phi \cdot m(u)\doteq \phi \circ m(u),u\in U$.

生成微分同胚的拉格朗日流和欧拉流

在刚体运动学研究中，低维矩阵李群一直是研究的重点。矩阵群是低维映射，是提供了坐标系间一一对应的微分同胚，且具有光滑的逆。旋转与标量的矩阵群可从闭形式的有限维矩阵生成，后者是简单常微分方程的解，由矩阵指数给出。

在研究计算解剖学中的可变形形状时，选择了更一般的微分同胚群，是到无限维的类推。计算解剖学用到的高维微分同胚群从满足拉格朗日与欧拉流场规范的光滑流$\phi _{t},t\in [0,1]$生成，满足常微分方程：

显示坐标$x\in X$的拉格朗日流与满足常微分方程${\dot {\phi }}_{t}=v_{t}(\phi _{t}),\phi _{0}=id$的相关向量场$v_{t},t\in [0,1].$

${\frac {d}{dt}}\phi _{t}=v_{t}\circ \phi _{t},\ \phi _{0}=id\ ;$

(拉格朗日流)

$v\doteq (v_{1},v_{2},v_{3})$是${\mathbb {R} }^{3}$上的向量场，称为粒子在流的位置$\phi$处的欧拉速度。向量场是函数空间中的函数，被模拟为高维光滑希尔伯特空间；流的雅各比量$\ D\phi \doteq ({\frac {\partial \phi _{i}}{\partial x_{j}}})$也是函数空间中的高维场，而非矩阵群中的低维矩阵。流首先作为图像匹配中的大变形被引入；${\dot {\phi }}_{t}(x)$是粒子x在t时刻的瞬时速度。

群所需的逆$\phi _{t}^{-1},t\in [0,1]$定义在具有平逆流的欧拉向量场上

${\frac {d}{dt}}\phi _{t}^{-1}=-(D\phi _{t}^{-1})v_{t},\ \phi _{0}^{-1}=id\ .$

(逆传输流)

计算解剖学的微分同胚群

微分同胚群特别大。为确保微分同胚的光滑流，避免逆出现类冲激的解，向量场必须在空间中至少1阶连续可微。对${\mathbb {R} }^{3}$上的微分同胚，向量场被模拟为希尔伯特空间$(V,\|\cdot \|_{V})$的元素，可用索博列夫嵌入定理实现，使元素都有严格大于2的广义平方可积空间导数（因此$v_{i}\in H_{0}^{3},i=1,2,3,$即可），从而得到一次连续可微函数。

微分同胚群是向量场在索博列夫范数下绝对可积的流：

$Diff_{V}\doteq \{\varphi =\phi _{1}:{\dot {\phi }}_{t}=v_{t}\circ \phi _{t},\phi _{0}=id,\int _{0}^{1}\|v_{t}\|_{V}dt<\infty \}\ ,$

(微分同胚群)

其中$\|v\|_{V}^{2}\doteq \int _{X}Av\cdot vdx,\ v\in V\ ,$ 线性运算A映射到对偶空间$A:V\mapsto V^{*}$，当$Av\in V^{*}$是对偶空间中的广义函数时，用分部积分法计算积分。

微分同胚度量：形状与形式的度量空间

更多信息：微分同胚度量

微分同胚群与流形、面间度量的研究一直是很重要的研究领域。微分同胚度量描述了两个图形或图像的间距；度量长度是将坐标系代入另一坐标系的流的最短长度。

通常，我们熟悉的欧氏度量不适用，因为形状与形式的模式不构成向量空间。在计算解剖学的黎曼轨道模型中，作用于形式$\phi \cdot m\in {\mathcal {M}},\phi \in Diff_{V},m\in {\mathcal {M}}$的微分同胚并不线性。定义度量的方法有很多，对与形状有关的集合可用豪斯多夫度量。我们用来诱导黎曼度量的方法是通过定义流的微分同胚坐标系变换间的度量长度，来诱导形状轨道上的度量。测量形状轨道中坐标系间的测地流长度，称为微分同胚度量。

微分同胚上的右不变度量

定义微分同胚群上的距离

$d_{Diff_{V}}(\psi ,\varphi )=\inf _{v_{t}}\left(\int _{0}^{1}\int _{X}Av_{t}\cdot v_{t}dx\ dt:\phi _{0}=\psi ,\phi _{1}=\varphi ,{\dot {\phi }}_{t}=v_{t}\circ \phi _{t}\right)^{1/2}\ ;$

(度量微分同胚)

这是微分同胚的右不变度量，由于$\forall \phi \in Diff_{V},$

$d_{Diff_{V}}(\psi ,\varphi )=d_{Diff_{V}}(\psi \circ \phi ,\varphi \circ \phi )$

所以空间的重参数化是不变的。

形状和形式的度量

关于形状和形式的距离，$d_{\mathcal {M}}:{\mathcal {M}}\times {\mathcal {M}}\rightarrow \mathbb {R} ^{+}$，

$d_{\mathcal {M}}(m,n)=\inf _{\phi \in \operatorname {Diff} _{V}:\phi \cdot m=n}d_{\operatorname {Diff} _{V}}(id,\phi )\ ;$

(形状形式度量)

图像用轨道表示为$I\in {\mathcal {I}}$及度量$,d_{\mathcal {I}}$。

微分同胚流上哈密顿原理的作用积分

经典力学中，物理系统的演化由与哈密顿原理的最小作用量原理相关的欧拉-拉格朗日方程描述。例如，这是获得自由粒子牛顿运动定律的标准方法；更广泛地说，欧拉-拉格朗日方程可用于广义坐标。计算解剖学中的欧拉-拉格朗日方程描述了微分同胚度量坐标系间的测地最短路径流，广义坐标是微分同胚的流，其拉格朗日速度$\phi ,{\dot {\phi }}$，两者通过拉格朗日速度$v\doteq {\dot {\phi }}\circ \phi ^{-1}$相关联。 生成欧拉-拉格朗日方程的哈密顿原理要求拉格朗日量上的作用积分为

$J(\phi )\doteq \int _{0}^{1}L(\phi _{t},{\dot {\phi }}_{t})dt\ ;$

(哈密顿-积分-拉格朗日量)

拉格朗日量由动能给出：

$L(\phi _{t},{\dot {\phi }}_{t})\doteq {\frac {1}{2}}\int _{X}A({\dot {\phi }}_{t}\circ \phi _{t}^{-1})\cdot ({\dot {\phi }}_{t}\circ \phi _{t}^{-1})dx={\frac {1}{2}}\int _{X}Av_{t}\cdot v_{t}\ dx\ .$

(拉格朗日量动能)

另见

• 计算神经科学