凸分析:修订间差异
标签:新重定向 |
新条目 标签:移除重定向 |
||
| 第1行: | 第1行: | ||
[[File:3dpoly.svg|thumb|right|3维凸多面体。凸分析不仅包括欧氏空间凸子集的研究,还包含抽象空间上凸函数的研究。]] |
|||
#REDIRECT [[凸優化]] |
|||
'''凸分析'''是研究[[凸函数]]与[[凸集]]性质的[[数学]]分支,其应用称作[[凸优化]],是[[最优化]]理论的子分支。 |
|||
== 凸集 == |
|||
{{main|凸集}} |
|||
某[[向量空间]]''X''的子集<math>C \subseteq X</math>,若满足下列任意一条等价条件,就称其是'''凸'''的(convex): |
|||
#若<math>0 \leq r \leq 1</math>是实数,<math>x, y \in C</math>,则<math>r x + (1 - r) y \in C.</math><ref name="Rockafellar" /> |
|||
#若<math>0 < r < 1</math>是实数,<math>x, y \in C,\ x \neq y,</math>则<math>r x + (1 - r) y \in C.</math> |
|||
[[Image:ConvexFunction.svg|thumb|300px|right|区间上的凸函数]] |
|||
{{main|凸函数}} |
|||
<math>f : X \to [-\infty, \infty]</math>始终是以[[扩展实数线]]<math>[-\infty, \infty] = \mathbb{R} \cup \{ \pm \infty \}</math>为值域、以某向量空间的凸子集<math>\operatorname{domain} f = X</math>为[[定义域]]的映射。 |
|||
映射<math>f : X \to [-\infty, \infty]</math>,若 |
|||
:<math>f( r x + (1 - r) y ) \leq r f(x) + (1 - r) f(y)</math>(凸性<math>\le</math>) |
|||
对所有实数<math>0 < r < 1</math>、所有<math>x, y \in X,\ x \neq y</math>都成立,称映射''f''是'''凸函数'''。若此不等式被替换为严格不等式 |
|||
:<math>f( r x + (1 - r) y ) < r f(x) + (1 - r) f(y)</math>(凸性<math><</math>) |
|||
对''f''仍成立,则称''f''是'''严格凸'''的。<ref name="Rockafellar" /> |
|||
凸函数与凸集有关。特别地,当且仅当函数''f''的[[上图 (数学)|上图(epigraph)]] |
|||
[[Image:Epigraph convex.svg|right|thumb|300px|当且仅当函数(黑色)的上图(即[[函数图像]]上方区域,绿色)是[[凸集]]时,函数是凸的。]] |
|||
[[Image:Grafico 3d x2+xy+y2.png|right|300px|thumb|二元凸函数<math>x^2 + x y + y^2</math>的图像]] |
|||
:<math>\operatorname{epi} f := \left\{ (x,r) \in X \times \mathbb{R} ~:~ f(x) \leq r \right\}</math> |
|||
是凸集时,函数''f''是凸的。{{sfn|Rockafellar|Wets|2009|pp=1-28}}扩展实值函数的上图在凸分析中的作用类似于实值[[函数图像]]在[[实分析]]中的作用。特别地,扩展实值函数的上图提供了几何直觉,可用于形式化或证明猜想。 |
|||
函数<math>f : X \to [-\infty, \infty]</math>的定义域记作<math>\operatorname{domain} f</math>,[[有效域]]则是集合{{sfn|Rockafellar|Wets|2009|pp=1-28}} |
|||
:<math>\operatorname{dom} f := \{ x \in X ~:~ f(x) < \infty \}.</math> |
|||
函数<math>f : X \to [-\infty, \infty]</math>,当且仅当<math>\forall x \in \operatorname{domain} f,\ f(x) > -\infty,\ \operatorname{dom} f \neq \varnothing</math>,称函数是[[真凸函数]]。{{sfn|Rockafellar|Wets|2009|pp=1-28}}这意味着在''f''的定义域中存在''x''使<math>f(x) \in \mathbb{R}</math>,''f''也永远不等于<math>f</math><math>-\infty</math>。换句话说,若函数的定义域非空、永远不取<math>-\infty</math>、不等于<math>+\infty</math>,则就是真凸函数。若<math>f : \mathbb{R}^n \to [-\infty, \infty]</math>是[[真凸函数]],则存在向量<math>\vec b \in \mathbb{R}^n</math>、实数<math>r \in \mathbb{R}</math>使得 |
|||
:<math>\forall x,\ f(x) \geq x \cdot b - r</math> |
|||
其中<math>x \cdot b</math>表示向量的[[点积]]。 |
|||
== 凸共轭 == |
|||
{{main|凸共轭}} |
|||
扩展实值函数<math>f : X \to [-\infty, \infty]</math>(不必凸)的凸共轭是来自''X''的(连续)[[对偶空间]]函数<math>f^* : X^* \to [-\infty, \infty]</math>{{sfn|Zălinescu|2002|pp=75-79}} |
|||
:<math>f^*\left(x^*\right) = \sup_{z \in X} \left\{ \left\langle x^*, z \right\rangle - f(z) \right\}</math> |
|||
其中,括号<math>\left\langle \cdot, \cdot \right\rangle</math>表示规范[[对偶系统|对偶性]]<math>\left\langle x^*, z \right\rangle := x^*(z)</math>。''f''的双共轭是映射<math>f^{**} = \left( f^* \right)^* : X \to [-\infty, \infty]</math>,定义为<math>\forall x\in X,\ f^{**}(x) := \sup_{z^* \in X^*} \left\{ \left\langle x, z^* \right\rangle - f\left( z^* \right) \right\}</math> |
|||
将''X''上的''Y''值函数记作<math>\operatorname{Func}(X; Y)</math>,则<math>f \mapsto f^*</math>定义的映射<math>\operatorname{Func}(X; [-\infty, \infty]) \to \operatorname{Func}\left( X^*; [-\infty, \infty] \right)</math>乘坐勒让德-芬切尔变换。 |
|||
=== 次微分集与芬切尔-扬不等式 === |
|||
若<math>x \in X,\ f : X \to [-\infty, \infty]</math>,则次微分集(subdifferential set)为 |
|||
:<math> |
|||
\begin{alignat}{4} |
|||
\partial f(x) |
|||
:&= \left\{ x^* \in X^* ~:~ f(z) \geq f(x) + \left\langle x^*, z - x \right\rangle \text{ for all } z \in X \right\} && (\text{“} z \in X \text{''} \text{ can be replaced with: } \text{“} z \in X \text{ such that } z \neq x \text{''}) \\ |
|||
&= \left\{ x^* \in X^* ~:~ \left\langle x^*, x \right\rangle - f(x) \geq \left\langle x^*, z \right\rangle - f(z) \text{ for all } z \in X \right\} && \\ |
|||
&= \left\{ x^* \in X^* ~:~ \left\langle x^*, x \right\rangle - f(x) \geq \sup_{z \in X} \left\langle x^*, z \right\rangle - f(z) \right\} && \text{ The right hand side is } f^*\left( x^* \right) \\ |
|||
&= \left\{ x^* \in X^* ~:~ \left\langle x^*, x \right\rangle - f(x) = f^*\left( x^* \right) \right\} && \text{ Taking } z := x \text{ in the } \sup{} \text{ gives the inequality } \leq. \\ |
|||
\end{alignat} |
|||
</math> |
|||
例如,在<math>f = \| \cdot \|</math>是''X''上的范数这一重要特例中,可以证明<ref group=proof><math>X = \{ 0 \}</math>则结论是直接的(平凡),所以假设不这样(非平凡)。固定<math>x \in X</math>,将''f''换成范数,给出<math>\partial f(x) = \left\{ x^* \in X^* ~:~ \left\langle x^*, x \right\rangle - \| x \| \geq \left\langle x^*, z \right\rangle - \| z \| \forall z \in X \right\}</math>。若<math>x^* \in \partial f(x),\ r \geq 0</math>是实数,则<math>z := r x</math>给出<math>\left\langle x^*, x \right\rangle - \| x \| \geq \left\langle x^*, r x \right\rangle - \| r x \| = r \left[ \left\langle x^*, x \right\rangle - \| x \| \right],</math>特别地取<math>r := 2</math>则有<math>x^*(x) \geq \| x \|</math>,而取<math>r := \frac1{2}</math>则有<math>x^*(x) \leq \| x \|</math>于是<math>x^*(x) = \| x \|</math>;若还<math>x \neq 0</math>则因<math>x^*\left(\frac{x}{\|x\|}\right) = 1,</math>由[[对偶范数]]的定义可知<math>\left\| x^* \right\| \geq 1.</math>由于<math>\partial f(x) \subseteq \left\{ x^* \in X^* ~:~ x^*(x) = \| x \| \right\},</math>其等价于<math>\partial f(x) = \partial f(x) \cap \left\{ x^* \in X^* ~:~ x^*(x) = \| x \| \right\},</math>可知<math>\partial f(x) = \left\{ x^* \in X^* ~:~ x^*(x) = \| x \| \text{ and } \| z \| \geq \left\langle x^*, z \right\rangle \text{ for all } z \in X \right\},</math>于是<math>\left\| x^* \right\| \leq 1,\ \forall x^* \in \partial f(x).</math>从这些事实,可以得到结论。∎</ref> |
|||
若<math>0 \neq x \in X</math>,则此定义可简化为: |
|||
:<math>\partial f (x) = \left\{ x^* \in X^* ~:~ \left\langle x^*, x \right\rangle = \| x \| \text{ and } \left\| x^* \right\| = 1 \right\}</math>;<math>\partial f(0) = \left\{ x^* \in X^* ~:~ \left\| x^* \right\| \leq 1 \right\}.</math> |
|||
<math>\forall x \in X,\ x^* \in X^*,\ f(x) + f^*\left(x^*\right) \geq \left\langle x^*, x \right\rangle,</math>这就是芬切尔-扬不等式,当且仅当<math>x^* \in \partial f(x)</math>时是等式。正是通过这种方式,次微分集<math>\partial f (x)</math>与凸共轭<math>f^*\left( x^* \right)</math>直接相关。 |
|||
=== 双共轭 === |
|||
函数<math>f : X \to [-\infty, \infty]</math>的双共轭是共轭的共轭,一般写作<math>f^{**} : X \to [-\infty, \infty]</math>。双共轭有助于显示[[强对偶]]或[[弱对偶]]何时成立(通过[[扰动函数]])。 |
|||
<math>\forall x \in X,</math>不等式<math>f^{**}(x) \leq f(x)</math>符合芬切尔-扬不等式。对[[真凸函数|紧合(proper)的函数]],[[当且仅当]]''f''是凸的[[下半连续]]函数时,<math>f = f^{**}</math>([[芬切尔–莫罗定理]])。{{sfn|Zălinescu|2002|pp=75-79}}<ref name="BorweinLewis" /> |
|||
== 凸最小化 == |
|||
{{main|凸最小化}} |
|||
凸最小化(主)问题形如 |
|||
:给定凸函数<math>f : X \to [-\infty, \infty]</math>与凸子集<math>M \subseteq X</math>,求<math>\inf_{x \in M} f(x)</math> |
|||
=== 对偶问题 === |
|||
{{main|对偶性 (最佳化)}} |
|||
优化理论中,对偶原则(duality principle)指出,优化问题可以从两个角度分别视作主问题与对偶问题。 |
|||
一般来说,给定一对分离的局部凸空间<math>\left(X, X^*\right)</math>、<math>\left(Y, Y^*\right)</math>,以及函数<math>f : X \to [-\infty, \infty]</math>,可以把主问题定义为求''x''使得 |
|||
:<math>\inf_{x \in X} f(x).</math> |
|||
可令<math>f = f + I_{\mathrm{constraints}}</math>(其中''I''是[[示性函数 (凸分析)|示性函数]])将约束嵌入''f''。那么让<math>F : X \times Y \to [-\infty, \infty]</math>是[[扰动函数]],使得<math>F(x, 0) = f(x)</math>。<ref name="BWG" /> |
|||
关于所选扰动函数的对偶问题由下式给出: |
|||
:<math>\sup_{y^* \in Y^*} -F^*\left(0, y^*\right)</math> |
|||
其中<math>F^*</math>是''F''两个变量的凸共轭。 |
|||
[[对偶间隙]]是不等式左右两式的差{{sfn|Zălinescu|2002|pp=106-113}}<ref name="BWG" /><ref name="Csetnek 2010" /> |
|||
:<math>\sup_{y^* \in Y^*} -F^*\left(0, y^*\right) \le \inf_{x \in X} F(x, 0).</math> |
|||
此原理同[[弱对偶]]。若两侧相等,则问题满足[[强对偶]]。 |
|||
强对偶成立的条件有很多,如 |
|||
* <math>F = F^{**}</math>,其中''F''是连接主问题与对偶问题的[[扰动函数]],<math>F^{**}</math>是''F''的双共轭;{{Citation needed|date=January 2012}} |
|||
* 主问题是[[线性规划]]问题; |
|||
* [[凸优化]]问题的[[斯莱特条件]]。<ref name="borwein" /><ref name="boyd" /> |
|||
==== 拉格朗日对偶性 ==== |
|||
对不等式约束的凸最小化问题, |
|||
:::<math>\min {}_{x} f(x)</math> subject to <math>g_i(x) \leq 0</math>,其中<math>i = 1, \ldots, m.</math> |
|||
其拉格朗日对偶问题是 |
|||
:::<math>\sup {}_{u} \inf {}_{x} L(x, u)</math> subject to <math>u_i(x) \geq 0</math>,其中<math>i = 1, \ldots, m.</math> |
|||
其中目标函数<math>L(x, u)</math>是如下定义的拉格朗日对偶函数: |
|||
:<math>L(x, u) = f(x) + \sum_{j=1}^m u_j g_j(x)</math> |
|||
== 另见 == |
|||
* [[凸性 (经济学)]] |
|||
** [[非凸 (经济学)]] |
|||
== 注释 == |
|||
{{reflist|30em|refs= |
|||
<ref name="borwein">{{cite book|last1=Borwein|first1=Jonathan|last2=Lewis|first2=Adrian|title=Convex Analysis and Nonlinear Optimization: Theory and Examples|edition=2|year=2006|publisher=Springer|isbn=978-0-387-29570-1}}</ref> |
|||
<ref name="BorweinLewis">{{cite book|last1=Borwein|first1=Jonathan|last2=Lewis|first2=Adrian|title=Convex Analysis and Nonlinear Optimization: Theory and Examples|url=https://archive.org/details/convexanalysisno00borw_812|url-access=limited|edition=2|year=2006|publisher=Springer|isbn=978-0-387-29570-1|pages=[https://archive.org/details/convexanalysisno00borw_812/page/n88 76]–77}}</ref> |
|||
<ref name="BWG">{{cite book|last1=Boţ|first1=Radu Ioan|last2=Wanka|first2=Gert|last3=Grad|first3=Sorin-Mihai|title=Duality in Vector Optimization|year=2009|publisher=Springer|isbn=978-3-642-02885-4}}</ref> |
|||
<ref name="boyd">{{cite book|last1=Boyd|first1=Stephen|last2=Vandenberghe|first2=Lieven|title=Convex Optimization|publisher=Cambridge University Press|year=2004|isbn=978-0-521-83378-3|url=https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf|access-date=2011-10-03}}</ref> |
|||
<ref name="Csetnek 2010">{{cite book|last=Csetnek|first=Ernö Robert|title=Overcoming the failure of the classical generalized interior-point regularity conditions in convex optimization. Applications of the duality theory to enlargements of maximal monotone operators|year=2010|publisher=Logos Verlag Berlin GmbH|isbn=978-3-8325-2503-3}}</ref> |
|||
<ref name="Rockafellar">{{cite book|last=Rockafellar|first=R. Tyrrell|author-link=Rockafellar, R. Tyrrell|title=Convex Analysis|publisher=Princeton University Press|location=Princeton, NJ|year=1997|orig-year=1970|isbn=978-0-691-01586-6}}</ref> |
|||
}} |
|||
{{reflist|group=proof}} |
|||
== 参考文献 == |
|||
* {{sfn|Bauschke|Combettes|2017|pp=1-2}} |
|||
* {{sfn|Boyd|Vandenberghe|2004|pp=1-2}} |
|||
* {{cite book|last1=Hiriart-Urruty|first1=J.-B.|author1-link=J.-B. Hiriart-Urruty|last2=Lemaréchal|first2=C.|author2-link=C. Lemaréchal|title=Fundamentals of convex analysis|publisher=Springer-Verlag |location=Berlin |year=2001 |isbn=978-3-540-42205-1}} |
|||
* {{cite book|last1=Kusraev|first1=A.G.|last2=Kutateladze|first2=Semen Samsonovich|author2-link=Semen Samsonovich Kutateladze|title=Subdifferentials: Theory and Applications|publisher=Kluwer Academic Publishers|year=1995|isbn=978-94-011-0265-0|location=Dordrecht}} |
|||
* {{sfn|Rockafellar|Wets|2009|p=}} |
|||
* {{sfn|Rudin|1991|p=}} |
|||
* {{cite book|last=Singer|first=Ivan|title=Abstract convex analysis|series=Canadian Mathematical Society series of monographs and advanced texts|publisher=John Wiley & Sons, Inc.|location=New York|year= 1997|pages=xxii+491|isbn=0-471-16015-6|mr=1461544}} |
|||
* {{cite book|last1=Stoer|first1=J.|last2=Witzgall|first2=C.|title=Convexity and optimization in finite dimensions |volume=1 |publisher=Springer |location=Berlin | year=1970 |isbn=978-0-387-04835-2}} |
|||
* {{sfn|Zălinescu|2002|pp=1-2}} |
|||
==外部链接== |
|||
* {{Commons category-inline}} |
|||
{{凸分析与变分分析}} |
|||
[[Category:凸分析| ]] |
|||
[[Category:凸几何|分析]] |
|||
2024年3月10日 (日) 20:09的版本

凸分析是研究凸函数与凸集性质的数学分支,其应用称作凸优化,是最优化理论的子分支。
凸集
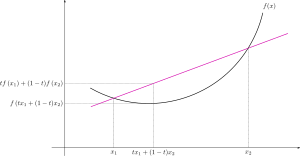
某向量空间X的子集,若满足下列任意一条等价条件,就称其是凸的(convex):
- 若是实数,,则[1]
- 若是实数,则
始终是以扩展实数线为值域、以某向量空间的凸子集为定义域的映射。 映射,若
- (凸性)
对所有实数、所有都成立,称映射f是凸函数。若此不等式被替换为严格不等式
- (凸性)
对f仍成立,则称f是严格凸的。[1] 凸函数与凸集有关。特别地,当且仅当函数f的上图(epigraph)


是凸集时,函数f是凸的。[2]扩展实值函数的上图在凸分析中的作用类似于实值函数图像在实分析中的作用。特别地,扩展实值函数的上图提供了几何直觉,可用于形式化或证明猜想。
函数,当且仅当,称函数是真凸函数。[2]这意味着在f的定义域中存在x使,f也永远不等于。换句话说,若函数的定义域非空、永远不取、不等于,则就是真凸函数。若是真凸函数,则存在向量、实数使得
其中表示向量的点积。
凸共轭
扩展实值函数(不必凸)的凸共轭是来自X的(连续)对偶空间函数[3]
其中,括号表示规范对偶性。f的双共轭是映射,定义为 将X上的Y值函数记作,则定义的映射乘坐勒让德-芬切尔变换。
次微分集与芬切尔-扬不等式
若,则次微分集(subdifferential set)为
例如,在是X上的范数这一重要特例中,可以证明[proof 1]
若,则此定义可简化为:
- ;
这就是芬切尔-扬不等式,当且仅当时是等式。正是通过这种方式,次微分集与凸共轭直接相关。
双共轭
函数的双共轭是共轭的共轭,一般写作。双共轭有助于显示强对偶或弱对偶何时成立(通过扰动函数)。
不等式符合芬切尔-扬不等式。对紧合(proper)的函数,当且仅当f是凸的下半连续函数时,(芬切尔–莫罗定理)。[3][4]
凸最小化
凸最小化(主)问题形如
- 给定凸函数与凸子集,求
对偶问题
优化理论中,对偶原则(duality principle)指出,优化问题可以从两个角度分别视作主问题与对偶问题。
一般来说,给定一对分离的局部凸空间、,以及函数,可以把主问题定义为求x使得
可令(其中I是示性函数)将约束嵌入f。那么让是扰动函数,使得。[5]
关于所选扰动函数的对偶问题由下式给出:
其中是F两个变量的凸共轭。
此原理同弱对偶。若两侧相等,则问题满足强对偶。 强对偶成立的条件有很多,如
拉格朗日对偶性
对不等式约束的凸最小化问题,
- subject to ,其中
其拉格朗日对偶问题是
- subject to ,其中
其中目标函数是如下定义的拉格朗日对偶函数:
另见
注释
- ^ 1.0 1.1 Rockafellar, R. Tyrrell. Convex Analysis. Princeton, NJ: Princeton University Press. 1997 [1970]. ISBN 978-0-691-01586-6.
- ^ 2.0 2.1 2.2 Rockafellar & Wets 2009,第1-28頁.
- ^ 3.0 3.1 Zălinescu 2002,第75-79頁.
- ^ Borwein, Jonathan; Lewis, Adrian. Convex Analysis and Nonlinear Optimization: Theory and Examples
 2. Springer. 2006: 76–77. ISBN 978-0-387-29570-1.
2. Springer. 2006: 76–77. ISBN 978-0-387-29570-1.
- ^ 5.0 5.1 Boţ, Radu Ioan; Wanka, Gert; Grad, Sorin-Mihai. Duality in Vector Optimization. Springer. 2009. ISBN 978-3-642-02885-4.
- ^ Zălinescu 2002,第106-113頁.
- ^ Csetnek, Ernö Robert. Overcoming the failure of the classical generalized interior-point regularity conditions in convex optimization. Applications of the duality theory to enlargements of maximal monotone operators. Logos Verlag Berlin GmbH. 2010. ISBN 978-3-8325-2503-3.
- ^ Borwein, Jonathan; Lewis, Adrian. Convex Analysis and Nonlinear Optimization: Theory and Examples 2. Springer. 2006. ISBN 978-0-387-29570-1.
- ^ Boyd, Stephen; Vandenberghe, Lieven. Convex Optimization (PDF). Cambridge University Press. 2004 [2011-10-03]. ISBN 978-0-521-83378-3.
参考文献
- [1]
- [2]
- Hiriart-Urruty, J.-B.; Lemaréchal, C. Fundamentals of convex analysis. Berlin: Springer-Verlag. 2001. ISBN 978-3-540-42205-1.
- Kusraev, A.G.; Kutateladze, Semen Samsonovich. Subdifferentials: Theory and Applications. Dordrecht: Kluwer Academic Publishers. 1995. ISBN 978-94-011-0265-0.
- [3]
- [4]
- Singer, Ivan. Abstract convex analysis. Canadian Mathematical Society series of monographs and advanced texts. New York: John Wiley & Sons, Inc. 1997: xxii+491. ISBN 0-471-16015-6. MR 1461544.
- Stoer, J.; Witzgall, C. Convexity and optimization in finite dimensions 1. Berlin: Springer. 1970. ISBN 978-0-387-04835-2.
- [5]
外部链接
| ||||||||||||||||||||||||||||||||||||||||||
- ^ Bauschke & Combettes 2017,第1-2頁.
- ^ Boyd & Vandenberghe 2004,第1-2頁.
- ^ Rockafellar & Wets 2009.
- ^ Rudin 1991.
- ^ Zălinescu 2002,第1-2頁.







![{\displaystyle f:X\to [-\infty ,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb5b80b60f448c0542dc59fd71f22b8ce01e8bc7)
![{\displaystyle [-\infty ,\infty ]=\mathbb {R} \cup \{\pm \infty \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f784980f597dae36b4d32c2a89de0a449e99aca8)















![{\displaystyle f:\mathbb {R} ^{n}\to [-\infty ,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef5a82ad74366531ce71d6fe571255b18f1d29a)




![{\displaystyle f^{*}:X^{*}\to [-\infty ,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e13a90d630d56ab231b9102f8c606db82843f54)



![{\displaystyle f^{**}=\left(f^{*}\right)^{*}:X\to [-\infty ,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3229c63ee01e8790a85b9f288eddca1b70746688)



![{\displaystyle \operatorname {Func} (X;[-\infty ,\infty ])\to \operatorname {Func} \left(X^{*};[-\infty ,\infty ]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e960704508725beb4b9514813c473cbdf955b5a)
![{\displaystyle x\in X,\ f:X\to [-\infty ,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/280c918a431cf422d4510515aaf1fba0cf68b095)









![{\displaystyle f^{**}:X\to [-\infty ,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f75a283b8a505414ded658aca363cd399a95d9ef)









![{\displaystyle F:X\times Y\to [-\infty ,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be0d8959e1b20e3299c0b75df57a15d0b809378)


















![{\displaystyle \left\langle x^{*},x\right\rangle -\|x\|\geq \left\langle x^{*},rx\right\rangle -\|rx\|=r\left[\left\langle x^{*},x\right\rangle -\|x\|\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1204d83ef8154fa2d3b747047d2804e35743fab1)











