壓縮感知
压缩感知(Compressed sensing),也被称为压缩采样(Compressive sampling)或稀疏采样(Sparse sampling),是一种寻找欠定线性系统的稀疏解的技术。压缩感知被应用于电子工程尤其是信号处理中,用于获取和重构稀疏或可压缩的信号。這個方法利用訊號稀疏的特性,相較於奈奎斯特理論,得以從較少的測量值還原出原來整個欲得知的訊號。核磁共振就是一個可能使用此方法的應用。这一方法至少已经存在了四十年,由于Emmanuel Candès、戴維·多諾霍、Justin Romberg和陶哲轩的工作,最近这个领域有了长足的发展。
概览[编辑]
信号处理领域中的一个常见问题就是从一系列的采样中重建原本的信号。一般而言,未被采样的部分信号,是不可能重建出來的。然而通过借助对于信号(性质)的预先了解或合理假设,完美地通过一系列采样重建原信号就成为了可能。随着科学的发展,数学家们逐步增进了如何作出合理假设的能力,并慢慢了解到在何种情况下可将这些假设一般化、推广化。
信号处理领域中的一次较早的突破是奈奎斯特采样定理的提出。这一定理证明了若信号的最高频率小于采样频率的一半,便可完美地从采样结果中恢复原本信号,因此定義了采样定理取樣頻率的下限。这种数据获取模式先采样再压缩,需要大量的时间压缩和空间存储数据,这限制了高速信号处理的发展,也给硬件的实时处理带来了极大的挑战。
在2006年左右,Emmanuel Candès、戴維·多諾霍、Justin Romberg和陶哲轩证明了在已知信号稀疏性的情况下,可能凭借较采样定理所规定更少的采样数重建原信号,这一理论也是压缩感知的基石。
正交基展開(orthogonal basis expansion)採用的是完全正交基(complete and orthogonal basis set)來進行展開,而壓縮感知採用的是过完备的非正交基集(over-complete and non-orthogonal basis set)來展開訊號。
範例[编辑]
傅立葉級數展开是正交基展开(orthogonal basis expansion)的方法:
if
Three-parameter atom expansion,Four-parameter atom (chirplet) expansion,
PSWF 展开則是过完备的非正交基集展开(over-complete and non-orthogonal basis expansion)的方法:
(t) 不构成一个完备的正交基集。
分類[编辑]
压缩感知希望处理的问题是:
假设 组成一个过完备的非正交基集
問題一[编辑]
我们希望最小化 ( 是 范数, 意指 的值不為0 的個數),使得:
問題二[编辑]
我们希望最小化 ,使得:
問題三[编辑]
限制 为 M,我们想要最小化:
方法[编辑]
方法一:匹配追踪(贪心算法)[编辑]
原子:
(归一化)
[第1步]输入:,初始化:
[第2步]找到最小化的m
[第3步]令
[第4步]
[第5步]
[第6步]檢查下列條件是否符合,若不符合,回到[第2步];若符合,則進到[第7步]
問題一:是否满足
問題二:是否满足
問題三:是否满足
[第7步]
方法二:基追踪(Basis Pursuit)[编辑]
将 范数改为 范数
問題一:
我们想要最小化 ,使得:
問題二:
我们想要最小化 ,使得:
問題三:
令,我们想要最小化:
問題定義[编辑]
一般來說,一個常見的線性系統問題,有m個方程式, n個未知數,可以被定義如下:
其中
在通訊系統之中,y是被收到的訊號,而s則是要被重建的訊號,一般來說會有以下兩種情況:
1.,也就是說方程式的數量大於等於未知數的數量,這種情況發生的時候就可以利用最小平方法去求得最接近的解,求得的解如下:
其中是伪逆矩阵。
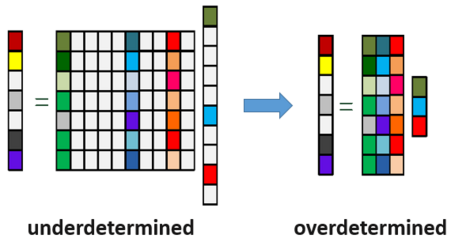
2.,也就是未知數的數量比方程式的數量來的多,这个方程组就被称为欠定线性系统,一般而言有无数个解,因此無法使用最小平方法去求得要重建的訊號。
但是,如果这个欠定线性系统只有唯一一个稀疏解,那么我们可以利用压缩感知理论和方法来寻找这个解。值得注意的是,並不是所有欠定线性方程组都具有稀疏解。
舉例來說,是一個欠定線性系統,會有無限多個解可以滿足這個方程式,然而若加入稀疏的限制条件:之間只有一個有值,其余都是0;就可以很輕易地得到這個欠定線性系統的解為,這個就是壓縮感知的最主要的精神所在。
從下圖可以輕易地了解,當解具有稀疏的特性時,就可以從欠定線性系統有無限多組解的情況變成可以利用最小平方法找出解的情況。
-
當訊號具有稀疏的特性時,線性系統就可以從無限多組解的情況,變成有解的情況。
稀疏性[编辑]
一個向量的稀疏性可以被定義如下:
的个数。
也就是計算一個向量之中非零的個數,舉例來說,如果,,因此目標的解就會變成如下:
希望能在非零個數越少的情況之下,找到最有可能的解。然而在实际中,最优化L0范数是一个NP难的问题,需要穷举s中非零值的所有排列可能,因而无法求解。通常采取的手段是对L1范数进行最优化求解,优化目标则变为:
或是使用匹配追踪系列算法、迭代阈值法以及专门处理二维图像问题的最小全变分法等求得次最优解的算法进行计算。
有限等距性質(Restricted Isometry Property, RIP)[编辑]
有限等距性質(RIP)是壓縮還原演算法中常常可以看見的名詞,主要可以被用來分析還原演算法的表現好壞。其定義如下:
其中的代表傳感矩陣,代表的是信號能量,可以表示如下:
因此整個式子可以視為信號跟傳感矩陣的相似程度,也就是做完轉換後的能量,要被RIP限制住,而RIP要求。
取样方法[编辑]
在理论上,为了确保信号重建的准确度,需要令所采用的取样矩阵各行列之间相干性(coherence)尽量地低,且须矩阵元素(element)取值随机性尽量地高。
相干性(coherence)可以簡單定義如下:
也就是取樣矩陣任兩個相異的行做內積後,取絕對值所產生的最大值,可以用來衡量信號重建的準確度。
而目前對於採樣矩陣有下列幾種選擇可以使還原重建度有一定品質:
- 對n個A的行向量在m維的單位半徑球面上進行隨機採樣
- 對任一個都採用相同獨立的高斯分布N(0,)進行隨機採樣
- 對任一個都採用如下式相同獨立的分布進行隨機採樣
除了上述的可能,現在也已經證實任何一個sub-gaussian的分布,都可以成為一個很好的測量矩陣,也就是說具有很好的還原效果。
而上述矩陣之所以常被拿來使用,主要是因為皆已經被驗證具有高機率性滿足有限等距性質,也就是相干性非常低,因此使用此方式進行訊號取樣後,仍可確保在信號具有足夠稀疏性的前提下得到較佳的壓縮感知重建效果。
且當使用上述矩陣時,只要訊號x的非零數目成下列關係,可以確保訊號被完美還原。
而C是一個根據不同情況而改變的常數。
但是在上述矩陣时,所需要的数据存储量过于庞大——每个矩阵元素都要单独记录,且数据类型一般为浮点数——这就促进了简化取样矩阵的研究;目前被提出的简化取样矩阵主要包括两种:结构简化采样矩阵与数值简化采样矩阵。
结构简化采样矩阵[编辑]
循環矩陣的形式為下式:
常對角矩陣的形式為下式:
,
其中。
可以發現到,若採用循環矩陣作為測量矩陣的話,只需要存取一列的矩陣元素;相反地,若使用常對角矩陣,除了第一列的矩陣元素外,需要額外儲存第一行的矩陣元素。
但是經過實驗發現,常對角矩陣的相干性是低於循環矩陣的,因此使用者可以依據自己的使用環境,來找到一個平衡點。
採用這兩種矩陣進行壓縮感知取樣時,可以大幅降低儲存成本,也為此算法的前端感測器大幅降低實現門檻。
数值简化采样矩阵[编辑]
数值简化采样矩阵普遍将原有的、按照高斯分布随机取值的采样矩阵元素以数值上更为简单的元素取代,但在分布上维持矩阵元素的分布随机性——即缩减了储存浮点数这一方面的成本。
一种较为基本的数值简化采样矩阵是0-1伯努利矩阵,其中的元素仅有0和1两种,分布模式为相同独立的伯努利分布(identical independent Bernoulli distribution)。
对于每一个矩阵元素,该分布的概率质量函数为:
求解/重构方法[编辑]
压缩感知利用了很多信号中所存在的冗余(换言之,这些信号并非完全是噪声)。具体而言,很多信号都是“稀疏”的;在适当的表示域中,它们的很多系数都是等于或约等于零。
在信号获取阶段,压缩感知在信号并不稀疏的域对信号进行线性测量。
为了从线性测量中重构出原来的信号,压缩感知求解一个称为L1-范数正则化的最小二乘问题。从理论上可以证明,在某些条件下,这个正则化最小二乘问题的解正是原欠定线性系统的稀疏解。
基追踪[编辑]
基追踪是一种信号重建演算法,被广泛地用于压缩感知领域,属于数学最优化问题的范畴,形式为。
其中s是n×1向量,表示输出(信号),y是m×1的测量向量,H是m×n的“转换矩阵”或稱作“测量矩阵”,其中M < N。
基追踪常在需要完美满足欠定线性方程组系统中时被应用,且要求解在L1基准下为最稀疏的。
若应用情景允许降低对完美恢复的要求,以换取更加稀疏的解s,降噪基追踪更为适用。
匹配追踪[编辑]
匹配追踪是一种稀疏近似运算,旨在找到多维数据在某个超完备字典(dictionary)上映射的“最佳匹配”。其基本的概念就是要用来自的函数组(称为基元,或atom)的加权和来表示希尔伯特空间上的信号:
其中表示被选取基元的序数,是每个基元的加权常数。对于固定的字典,匹配追踪会先找到与信号间内积最大的一个基元,再减去该基元带来的影响,然后重复找寻影响力次大的基元直到信号被较好地分解。
相较而言,以傅里叶级数表示的信号来说,字典是构建于正弦基函数之上的。信号处理领域中傅里叶分析的主要缺点就在于它只能提取出信号中常存的特征,而不能适应当前的分析目标信号。
若采用一组极端保险、带有大量冗余的字典,我们就能够找到可以完美匹配信号的函数组。在对信号进行编码与压缩时,最好是能够找到一组映射,使加权和中的大部分系数都接近零(具有“稀疏性”)。
正交匹配追蹤[编辑]
正交匹配追蹤(Orthogonal Matching Pursuit)是匹配追蹤的特殊形式,正交匹配追蹤的算法與匹配追蹤相同,但是正交匹配追蹤不會重複使用同一個基元來進行匹配,因此會比匹配追蹤更快收斂。
迭代閾值算法[编辑]
迭代閾值算法(Iterative Shrinkage-Thresholding Algorithm)是上述基於貪婪演算法(Greedy Algorithm)之匹配追蹤與正交匹配追蹤的替代算法,迭代算法主要是透過不斷的投影和取閾值來進行收斂,而他在每次迭代中,都還可以進行其他優化例如:Wigener 濾波,不僅可以降低運算複雜度,也可以提高還原品質。
正交匹配追蹤(Orthogonal Matching Pursuit)[编辑]
正交匹配追蹤是一個用來解決壓縮感知問題的演算法,在一定的複雜度之下有不錯的表現,他背後最主要的想法是源自於貪婪演算法(Greedy Algorithm),以下將逐步解說。
首先這個問題被定義為:y=Ax,目標是要藉由已知的y向量、A矩陣,來還原x向量,他會利用疊代的方式,逐步找出x向量當中最有可能是非零的位置。
一開始會有一個空集合,以及剩餘的部分,每次疊代都會從找出一個A矩陣投影到剩餘有最大值的位置,把這個位置加到之中,並從當中移除,最後再更新剩餘。利用疊代的方式,不斷地找出x向量當中最有可能非零的位置,直到達到演算法停止條件。
-
正交匹配追蹤演算法
在正交匹配追踪算法的基础上,Needell等人提出了正则正交匹配追踪(Regularized Orthogonal Matching Pursuit,ROMP)算法对于所有满足约束等距性条件的矩阵和所有稀疏信号进行重构。之后,引入回溯思想的压缩采样匹配追踪(Compressive Sampling Matching Pursuit,CoSaMP)算法被提出。
在实际应用中,稀疏信号非零元素个数K往往是未知的,而上述的匹配追踪算法都是建立在稀疏度K已知的基础上,因此出现了对K自适应的稀疏自适应匹配追踪(Sparsity Adaptive Matching Pursuit,SAMP)算法,它通过固定步长来逐步逼近进行重建,可以在稀疏度K未知的情况下获得较好的重建效果。
迭代閾值算法(Iterative Shrinkage-Thresholding Algorithm)[编辑]
迭代閾值算法是從Relaxation Method啟發而來,Relaxation Method是用於解決具有稀疏性的線性系統。
在迭代閾值算法中,問題一樣是被定義為:
而在此算法中,每一次的迭代主要分成兩部分:1、尋找新的解。2、更新殘值。 第一階段,主要是利用投影的方式找到更新的向量方向,再透過取閾值的方式來進行優化。
而是relaxation parameter,且。
而就是閾值函數(thresholding function),主要就是為了使迭代的過程中,逐漸逼近具有稀疏性性質的解,而目前主要有兩大類取閾值的方式:硬閾值函數(Hard Thresholding Function)與軟閾值函數(Soft Thresholding Function)。
硬閾值函數就是將小於閾值(thr)的解,一律通通過濾成0。
而軟閾值函數則是使用較為平滑的方式,將值逼近於稀疏性的解
,而是指示函數
而第二階段,則是利用新算出來的來進行殘差更新。
之後一直等到規定的迴圈數抵達即完成還原。
而此算法是Landweber iteration的變形,若沒有加入閾值函數的話,就會收斂到。
稀疏性空間投影[编辑]
壓縮感知還原演算法包括整個壓縮感知都是建立在信號有稀疏性上,但是並不是所有的信號都天然具有稀疏性,例:聲音。那麼是否不具有稀疏性的信號就不能使用壓縮感知呢?答案為並不是,天然不具有稀疏性的信號還是能夠使用壓縮感知,只需要把該信號投影到其他空間,其他該信號有稀疏性的空間下,壓縮感知就可直接使用在該投影空間上。可以被定義如下:
s:要被重建的訊號(原信號);ψ:投影矩陣,把非稀疏性信號投影到稀疏性空間;z:非零項遠小於零項
故原壓縮感知公式定義也隨之改變:
所以可以把視為原本壓縮感知公式裡面的H,還原演算法即可一樣使用。
至於的選擇對於不同信號來說有很多種,有離散餘弦變換(DCT) ,離散小波變換(DWT),字典學習(Dictionary Learning)等。
離散餘弦變換和離散小波變換[编辑]
利用信號經過這兩種變換後都會有稀疏性的特性,把這兩種變換變成矩陣形式,讓信號直接投影到具有稀疏性的空間上。
好處
- 不需要特別針對信號做不同的選擇,對於絕大部分信號可以直接使用。
- 並不需要前處理,可以直接使用。
壞處
- 限制了原信號的維度,必須滿足n = ,x為任意正整數。
- 因為通用所有信號,故經過壓縮感知還原演算法後還原的信號品質較差。
字典學習[编辑]
顧名思義即把當作一本要學習的字典,不斷的利用該信號和還原演算法後的結果做字典的更新,直到找到一個能夠把該信號投影到稀疏性空間上。
字典學習的流程:
- 設定字典學習的學習次數(Iter)
- 收集一定量(L筆)要學習的資料s,組成S = [s1, s2, ... ,sL]
- 固定,利用還原演算法找出每一筆資料的z,組成Z = [z1, z2, ... ,zL]
- ||S - Z| s.t. ||zi||0 < Kth i
- 固定Z, 利用3.所得之Z來更新字典
- 當Z固定時,定義誤差ei = si - zi,組成E = [e1, e2, ... ,eL]
- 所以整體的均方误差為 ||E|= || [e1, e2, ... ,eL] | = || S - Z|
- 在Z固定下使得E最小,將得到關係式 (S - Z)ZT = 0
- => = SZT(ZZT)-1
- 檢查Z上面是否已經有稀疏性,如有則結束學習;如沒有則回到3.直到達到學習的次數
字典學習的演算法有很多,較為常用的有Method of optimal directions(MOD[1])。
好處
- 因為針對該種類信號做學習,故還原後的品質較好。
- 對原信號的維度並沒有任何限制。
壞處
- 需要事前收集該種類的信號做學習,不能未學習直接使用。
- 因為針對該種類信號做學習,故直接使用在不同種類信號效果較差/不適用。
相關應用[编辑]
压缩感知与包括欠定系统、群验、稀疏编码、复用、稀疏采样等。在成像科技领域,亦有许多技术如(编码孔与计算摄影学)与压缩感知相关。亦有许多在不同技术完成度下将压缩感知实现的案例。
摄影学[编辑]
压缩感知技术被用于手机摄像头传感器设计中。这一技术使得在获取图像时所耗费的能量大大降低,可达原先耗费的15分之一——当然,需要引入复杂的解压算法;这一运算可能会需要脱机状态下的预先安装、设置。
压缩感知亦被用于实现单像素摄影。贝尔实验室运用了这一技术,用无镜片单像素相机在栅格中随机选取的孔隙处拍照,以达到成像效果。随着拍照次数的逐渐增多,照片质量也会逐步提高;一般来说,这种技术较之传统的摄影成像技术仅仅需要一小部分的数据占用量,且能完全避免与镜片或聚焦相关的故障或失常;参见[1] (页面存档备份,存于互联网档案馆) 。
全息成像[编辑]
压缩感知可被用于增加通过单幅全息图中所能得到的立体像素的数量改进全息摄影技术中的图像重建问题。在光学全息图或毫米波全息图采样率不足的情况下,这一技术也能够被用于图像检索以作出改善。
面部识别[编辑]
压缩感知目前被用于面部识别应用之中,参见Engineers Test Highly Accurate Face Recognition (页面存档备份,存于互联网档案馆)。
核磁共振成像[编辑]
壓縮感知也被應用在醫療影像上,特別是核磁共振成像(Magnetic Resonance Imaging, MRI),具有稀疏的特性,因此能使用壓縮感知的技術。在過去核磁共振成像會因為物理學、生理學上的限制,而有掃描時間較長的問題,如今壓縮感知利用核磁共振成像具有的稀疏特性,來改善成像品質以及降低所需要量測數量,能有效縮短核磁共振的掃描時間,近期相關的壓縮感知演算法也被廣為討論,可以參見[2] (页面存档备份,存于互联网档案馆) 、[3] (页面存档备份,存于互联网档案馆) 與[4] (页面存档备份,存于互联网档案馆),其中涉及的重建方法包括ISTA、FISTA、SISTA等。
地震成像[编辑]
一般來說地震成像既不稀疏,也不可壓縮,具有高維度、大面積的特性,因此會耗費大量的量測以及運算時間,所以希望能降低取樣的次數,同時能保有原本的品質。因此有人利用壓縮感知技術將取樣以及編碼同時進行,來達到降低維度的目的,最後再透過壓縮感知的還原演算法進行還原,可以參考[2]。
類比信息轉換(Analog-to-Information Converter, AIC)[编辑]
在通訊系統當中會遇到高頻寬的問題,因此會需要較高的取樣頻率,然而其中的信號可能含有的資訊是遠小於頻寬的,因此就會浪費軟、硬體的資源來進行取樣。所以有人提出用類比信息轉換(Analog-to-Information Converter, AIC)取代類比數位轉換(Analog-to-Digital Converter, ADC),利用隨機解調(Random Demodulation)的方式,來降低所需要的取樣次數,對於在時頻上有稀疏特性、寬頻的信號特別適合,可以參考[3]。
网络诊断[编辑]
压缩感知在被用于旨在利于网络管理的网络诊断应用中时带来了极佳成效。对网络延时的估计和网络拥塞的探知均可被归纳、建模为非定性的线性方程组系统,其中的参数矩阵正是所分析网络的路由选择矩阵。此外,在互联网情景中,网络路由矩阵常常能够满足压缩感知技术所要求的几个基本要素:低相关性、稀疏性及(可能的)R.I.P条件,请参见[5] (页面存档备份,存于互联网档案馆) 。
短红外摄影[编辑]
目前,基于压缩感知技术的商用短红外相机已被推出[6] (页面存档备份,存于互联网档案馆) 。这些相机的光敏度大约从0.9µm到1.7µm,在上述波段上,人类的肉眼是无效的。
通訊通道估測[编辑]
隨著通訊要求的頻寬越來越大,因此可用的頻帶從微波(Microwave)轉到毫米波(mmWave)的頻段,雖然可用的頻寬增加,然而會受到更嚴重的通道衰減,所以波束成型的技術被提出,結合天線陣列來對抗通道衰減的效應。然而大量的天線陣列會使得做通道估測的複雜度上升,傳統的做法是使用最小平方法(Least Square, LS)來進行通道估測,不過有人發現通道具有稀疏的特性,因此提出了利用壓縮感知的技術,進行壓縮通道估測(Compressed Channel Estimation, CCS),相較最小平方法,不僅複雜度降低,還能達到更低的錯誤率以及延遲性。
信号源定位[编辑]
利用压缩感知理论可以恢复出稀疏信号的特性,压缩感知理论被广泛应用于波达方向估计(Direction of Arrival,DOA)中。基于压缩感知的波达方向估计中将信号源矩阵看作是一个稀疏矩阵,在已知采样矩阵和阵列流形矩阵为前提下,对稀疏信号源矩阵进行重构以获得被测量信号源的波达方向。使用这种方法,不仅避免了传统波达方向估计中需要计算复杂协方差矩阵的步骤,同时还对空间中的相干信号源有着很好的性能。
物聯網[编辑]
在物聯網的情境之下,裝置的數量會大幅增加,然而因為資源有限,所以用來辨別裝置的展頻碼(m)會少於裝置的數量(n),因此會使得整個系統變成欠定的線性系統,然而這些裝置大部分的時候都是處於休息、監測的狀態,並不會一直傳送訊息給基地台,因此就有了稀疏的性質,利用壓縮感知的技術就能分辨出處於活動狀態的裝置,並解出其所傳送的訊號。
加密[编辑]
壓縮感知演算法天生就具有加密的性質,因為要重建原本信號的話,必須要知道採樣矩陣才能進重建。因此現今也有許多加密的研究關注於壓縮感知演算法,因為虛擬亂數傳感矩陣(Pseudo-random Sensing Matrix)可以被視為一組加密後的鑰匙,能對信號進行壓縮並同時加密,而不需要額外的運算,可以參考[4]。
參考資料[编辑]
- Candès, E.J., & Wakin, M.B., An Introduction To Compressive Sampling, IEEE Signal Processing Magazine, V.21, March 2008
- J. Choi et al., "Compressive Sensing for Wireless Communications: Useful Tips and Tricks", IEEE Commun. Survey and Tutorials.
- C. Bockelmann, H. F. Schepker, and A. Dekorsy, "Compressive sensing based multi‐user detection for machine‐to‐machine communication," Transactions on Emerging Telecommunications Technologies, vol. 24, no. 4, pp. 389-400, 2013.
- F. Monsees, C. Bockelmann, D. Wubben, and A. Dekorsy, "Sparsity aware multiuser detection for machine to machine communication," 2012 IEEE Globecom Workshops, Anaheim, CA, 2012, pp. 3-7.
- Shen Q, Liu W, Cui W, et al. "Underdetermined DOA Estimation Under the Compressive Sensing Framework: A Review". IEEE Access, 2016: 8865-8878.
- Jian-Jiun Ding, “Time Frequency Analysis and Wavelet Transforms ”, NTU, 2021.
外部链接[编辑]
- "The Fundamentals of Compressive Sensing" Part 1 (页面存档备份,存于互联网档案馆), Part 2 (页面存档备份,存于互联网档案馆) and Part 3 (页面存档备份,存于互联网档案馆): video tutorial by Mark Davenport, Georgia Tech. at SigView, the IEEE Signal Processing Society Tutorial Library.
- Using Math to Turn Lo-Res Datasets Into Hi-Res Samples (页面存档备份,存于互联网档案馆) Wired Magazine article
- Compressive Sensing Resources at Rice University.
- Compressed Sensing Makes Every Pixel Count (页面存档备份,存于互联网档案馆) – article in the AMS What's Happening in the Mathematical Sciences series
- Wiki on sparse reconstruction. [2014-06-24]. (原始内容存档于2015-05-04).
- ^ Engan, K.; Aase, S.O.; Hakon Husoy, J. Method of optimal directions for frame design. 1999 IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings. ICASSP99 (Cat. No.99CH36258) (IEEE). 1999. ISBN 0780350413. doi:10.1109/icassp.1999.760624.
- ^ Hennenfent, Gilles; Herrmann, Felix J. Simply denoise: Wavefield reconstruction via jittered undersampling. GEOPHYSICS: V19–V28. [2017-12-16]. doi:10.1190/1.2841038. (原始内容存档于2018-06-09).
- ^ Laska, J. N.; Kirolos, S.; Duarte, M. F.; Ragheb, T. S.; Baraniuk, R. G.; Massoud, Y. Theory and Implementation of an Analog-to-Information Converter using Random Demodulation. 2007 IEEE International Symposium on Circuits and Systems. May 2007: 1959–1962. doi:10.1109/ISCAS.2007.378360.
- ^ Orsdemir, A.; Altun, H. O.; Sharma, G.; Bocko, M. F. On the security and robustness of encryption via compressed sensing. MILCOM 2008 - 2008 IEEE Military Communications Conference. November 2008: 1–7 [2017-12-16]. doi:10.1109/MILCOM.2008.4753187. (原始内容存档于2021-02-24).








































![{\displaystyle s=[0\ 0\ 1\ 0\ 1\ 0\ 0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dd6b8b84669f50c7cd1252cb3c0f84c43916680)



















![{\displaystyle f(k;p)={\begin{cases}p&{\text{if }}k=1,\\[6pt]1-p&{\text{if }}k=0.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d45357d81684dfbff51e5d56e3fc2363b25a16)




































