相干性

在物理學裏，相干性 （coherence） 指的是，為了產生顯著的干涉現象，波所需具備的性質。更廣義地說，相干性描述波與自己波、波與其它波之間對於某種內秉物理量的關聯性質。

當兩個波彼此相互干涉時，因為相位的差異，會造成建設性干涉或摧毀性干涉。假若兩個正弦波的相位差為常數，則這兩個波的頻率必定相同，稱這兩個波「完全相干」。兩個「完全不相干」的波，例如白炽灯或太陽所發射出的光波，由於產生的干涉圖樣不穩定，無法被明顯地觀察到。在這兩種極端之間，存在著「部分相干」的波。

相干性又大致分類為時間相干性與空間相干性。時間相干性與波的頻寬有關；而空間相干性則與波源的有限尺寸有關。

波與波之間的的相干性可以用相干度（degree of coherence）來衡量。干涉可見度（interference visibility）是波與波之間的干涉圖樣的輻照度對比，相干度可以從干涉可見度計算出來。

波源

一般而言，互相不關聯的波源無法形成可觀察到的干涉圖樣。例如白炽灯或太陽是由很多互相不關聯、持續生成的微小發光點所組成，每一個發光點只會作用一段時間 $\Delta t\approx 10^{-8}-10^{-9} sec$ ，發射出一個有限長度的波列，之後，再也不會發光，但在其它位置，又會出現新的發光點。為了要能拍攝到這類光源所產生的由兩個波列疊加形成的干涉圖樣，攝影儀器的曝光時間必須要小於 $\Delta t$。在舊時，無法製造出這麼高階的攝影儀器，因此從這類光源很難拍攝到干涉圖樣。但是，通過適當處理，仍舊可以觀察到這些光源的干涉圖樣。

為了要觀察到這些互相不關聯的波源所形成的干涉圖樣，必須從這些波源製造出相干性較高的波。有兩種方法可以達成這目標：

1. 第一種方法稱為「波前分割法」。從微小波源發射出的波，其波前與微小波源之間的距離大致相等。使用具有幾條狹縫的檔板來過濾從微小波源發射出的波，只要這些狹縫與微小波源之間的距離相等，就可以保證同樣的波前入射於這幾條狹縫。位於波前的每一點都可以視為一個波源，會發射出次波。因此，從這幾條狹縫衍射出來的次波，其相位大致相同。楊氏雙縫實驗就是藉著這方法製成兩束相干性較高的光波，這兩束光波會在觀察屏產生干涉圖案。
2. 第二種方法稱為「波幅分割法」。用半透射、半反射的半鍍銀鏡，可以將光波一分為二，製造出透射波與反射波，這兩束光波非常相似，相干性非常高。假設這兩束光波的光程長度不相等，則由於在觀察屏的相位不同，會產生明顯不同的干涉圖樣。邁克生干涉儀使用的就是這種方法。

自從激光、激微波的發明以後，物理學者不再為尋找高相干性的光源這問題而煩惱，激光所製造出來的波列通常能維持 $\Delta t\approx 10^{-3} sec$ 之久。這給予足夠的曝光時間來拍攝干涉圖樣。

應用

以前，只有在學習光學的楊式雙縫實驗時，才會接觸到相干性這術語。現今許多涉及波動的領域，像聲學、電子工程、量子力學等等，都會使用到這術語。許多科技的運作都倚賴相干性質為基礎。例如，全像攝影術、音波相位陣列、光學相干斷層掃描、天文光學干涉儀 (astronomical optical interferometers) 、與射電望遠鏡、等等。

相干性與關聯性

兩個波彼此之間的關聯導致這兩個波彼此之間的相干性，又稱互相干性。這關聯是由交叉關聯函數來衡量。交叉關聯函數衡量從一個波預測另一個波的能力。

舉例而言，設想在所有時間完全關聯的兩個波。在任意時間，假若一個波發生任何變化，則另一個波也會做出同樣的變化；假若結合在一起，在所有時間，它們都會展示出完全建設性干涉或完全摧毀性干涉，則它們是完全相干。如稍後所述，第二個波不需要是另外一個實體，它可能是在不同時間或不同位置的第一個波。這案例所涉及的關聯稱為「自相干性」；對於這案例，可以用自關聯函數來衡量自相干性。

嚴格定義

假設在點S₁、點S₂的波擾分別為 $\tilde{E}_1(t)$ 、$\tilde{E}_2(t)$ （波浪號代表複數），則其交叉關聯函數 $\tilde{\Gamma}_{12}(\tau)$ 為

$\tilde{\Gamma}_{12}(\tau)=\langle\tilde{E}_1(t)\tilde{E}_2^{\,*}(t+\tau)\rangle \ \stackrel{def}{=}\ \lim_{T\rightarrow\infty}\frac{1}{T}\int_0^T \tilde{E}_1(t)\tilde{E}_2^{\,*}(t+\tau)\mathrm{d}t$ ；

其中，書名號表示取時間平均值，$T$ 是平均的時間間隔。

交叉關聯函數又稱為「互相干函數」。理論而言，必需取 $T$ 趨向於無窮大的極限；然而，實際而言，只要平均的時間間隔比相干時間（大約是有限長度的波列通過某固定點的有限時間）長久很多就行了。假設兩個波 $\tilde{E}_1(t)$ 、$\tilde{E}_2(t)$ 是同相單色波，則互相干函數 $\langle\tilde{E}_1(t)\tilde{E}_2^{\,*}(t)\rangle$ 必定大於0；假設兩個波 $\tilde{E}_1(t)$ 、$\tilde{E}_2(t)$ 是異相單色波，則互相干函數 $\langle\tilde{E}_1(t)\tilde{E}_2^{\,*}(t)\rangle$ 必定小於0。

「準單色波」是由一系列有限長度、隨機相位的波列組成。假設兩個波都是準單色波。則由於乘積 $\tilde{E}_1(t)\tilde{E}_2^{\,*}(t)$ 隨著兩個波列相位的不同而改變，有時大於0，有時小於0，經過時間平均，互相干函數會變得相當微小，可以近似為0。

從交叉關聯函數的定義式，可以衍生出自關聯函數，又稱為「自相干函數」。波 $\tilde{E}_1(t)$ 與延遲時間 $\tau$ 的自己波，兩者之間的自相干函數為

$\tilde{\Gamma}_{11}(\tau)=\langle\tilde{E}_1(t)\tilde{E}_1^{\,*}(t+\tau)\rangle$ 。

歸一化的互相干函數為

$\tilde{\gamma}_{12}(\tau)=\frac{\tilde{\Gamma}_{12}(\tau)}{\sqrt{\tilde{\Gamma}_{11}(0)\tilde{\Gamma}_{22}(0)}} =\frac{\langle\tilde{E}_1(t)\tilde{E}_2^{\,*}(t+\tau)\rangle}{\sqrt{\langle|\tilde{E}_1(t)|^2\rangle \langle|\tilde{E}_2(t)|^2\rangle}}$ 。

$\tilde{\gamma}_{12}(\tau)$ 又稱為兩個波的「複相干度」。從柯西-施瓦茨不等式可以推導出 $|\tilde{\gamma}_{12}(\tau)|\le 1$ 。絕對值 $|\tilde{\gamma}_{12}(\tau)|$ 就是相干度。當 $|\tilde{\gamma}_{12}(\tau)|=1$ 時，波 $\tilde{E}_1$ 與波 $\tilde{E}_2$ 完全相干；當 $|\tilde{\gamma}_{12}(\tau)|=0$ 時，兩個波完全不相干；當 $0< |\tilde{\gamma}_{12}(\tau)|< 1$ 時，兩個波部分相干。

本圖展示各種干涉圖樣的明暗條紋的清晰程度與干涉可見度的關係。縱軸是輻照度除以最大輻照度，橫軸是空間坐標。

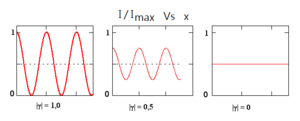
「干涉可見度」衡量干涉圖樣的明暗條紋的清晰程度，以方程式定義，

$\mathcal{V} = \frac{I_{max} - I_{min}}{I_{max} + I_{min}}$ ；

其中，$I_{max}$ 、$I_{max}$ 分別為干涉圖樣的最大輻照度與最小幅照度。

干涉可見度的范围在0到1之间。假設兩個波的振幅相等，則干涉可見度等於相干度：

$\mathcal{V} = |\tilde{\gamma}_{12}(\tau)|$ 。

各種波動實例

下述這些波的共同之處是，它們的物理行為可以用波動方程式或推廣的波動方程式來描述：

• 繩索的機械波。
• 液體的表面波。
• 電纜的電磁波。
• 聲波。
• 無線電波與微波。
• 光波。
• 量子尺寸粒子的物質波。

這些種類的波的物理行為，大多數可以直接測量獲得。因此，波與波之間的互相干函數可以很簡單地求得。但是，在光學裏，不能直接的測量電磁場，因為電磁場的震盪太快，比任何偵測器的時間分辨率還要快。可行之道是測量光波的輻照度。

大多數在這條目提到的涉及相干性的概念，都是先在光學領域發展成功，然後再適應於其它領域。因此，許多相干性測量標準都是採用間接地測量，甚至在可以直接測量的領域，都是這樣做。

時間相干性

圖 1 ：本圖顯示出，一個單色波的振幅（紅色），與延遲了時間 $\tau$ 的自己波的振幅（綠色），這兩個振幅隨著時間 $t$ 的演進而變化。這兩個波的相干時間是無窮大。因為，對於所有可能延遲時間 $\tau$ ，它們是完全關聯的。

圖 2 ：本圖顯示出，一個相位顯著飄移的準單色波的振幅（紅色，相干時間為 $\tau_c$ ），與延遲了時間 $2\tau_c$ 的自己波的振幅（綠色），這兩個振幅隨著時間 $t$ 的演進而變化。在任何給定時間 $t$ ，紅色波會與綠色波互相干涉。但是由於一半時間，紅色波與綠色波同相，另一半時間，兩個波異相，所以，對於這延遲，經過時間平均後，自相干函數可以近似為0。

一個波 $\tilde{E}_1(t)$ 與延遲了時間 $\tau$ 的自己波，兩者之間的自相干函數 $\tilde{\Gamma}_{11}(\tau)$ ，可以用來衡量時間相干性。對應的複相干度為 $\tilde{\gamma}_{11}(\tau)$ ，又稱為「複時間相干度」。時間相干性可以表達波源的單色性質，可以衡量一個波在延遲某時間後干涉自己的能力，因此又稱為「縱向相干性」。經過一段延遲時間 $\tau$ 後，假若一個波的相位或波幅開始發生足夠顯著的變化（因此自相干函數開始顯著地減小），則定義此延遲時間為「相干時間」 $\tau_c$ 。有限長度的波列通過某固定點的有限時間大約是相干時間。當 $\tau=0$ 時，一個波 $\tilde{E}_1(t)$ 與自己的相干度為 $|\tilde{\gamma}_{11}(0)|=1$ ；而當 $\tau\ge \tau_c$ 時，相干度 $|\tilde{\gamma}_{11}|$ 會顯著地減小，顯示在觀察屏的干涉圖樣也會變得模糊不清。「相干長度」 $L_c$ 定義為，在相干時間 $\tau_c$ 內，波所能傳播的距離，又稱為「縱向相干長度」。

相干時間與頻寬的關係

由於周期的倒數是頻率，一個波在越短時間內，變的不自相干（ $\tau_c$ 越小），則波的頻寬 $\Delta f$ 越大。兩個物理量的關係方程為

$\tau_c \Delta f \approx 1$ 。

用波長 $\lambda=c/f$ 來表達，

$\frac{L_c \Delta \lambda}{\lambda^2} \approx 1$ 。

用數學表述，這結果可以從傅立葉變換推導出來。自相干函數的傅里葉變換就是功率譜（power spectrum）（每個頻率的輻照度）。

實例

試想下述四個關於時間相干性的實例：

• 對於任何時間間隔，一個單色波都是完全的自相干（參閱圖 1 ）。
• 反過來說，一個相位迅速飄移的波，其相干時間必定很短（參閱圖 2 ）。
• 類似地，具有較寬頻域的脈衝波（pulse wave）（一種波包），由於振幅迅速地變化，所以，相干時間很短。
• 白光擁有非常寬的頻域，是一種振幅與相位都迅速變化的波。由於相干時間很短（ 10 週期左右），常被稱為「不相干波」。

雷射通常是最單色的光源。高度的單色性意味著長相干長度（長到幾百公尺）。例如，一個穩定的氦氖雷射 (helium-neon laser) ，能夠生產相干長度超過 $5 m$ 的光。可是，並不是所有的雷射都是單色的，例如，鈦藍寶石雷射 (Ti-sapphire laser) 光的 $\Delta \lambda \approx 2\ nm\ - \ 70\ nm$ 。發光二極體的光的 $\Delta \lambda \approx 50\ nm$ ，鎢絲燈光的 $\Delta \lambda \approx 600\ nm$ 。這些光源的相干時間都低於大多數的單色雷射。

全像攝影術需要長相干時間的光。相對比較，光學相干斷層掃描使用短相干時間的光。

測量方法

圖 3 ：本圖顯示出，一個波包的振幅（紅色）與延遲了時間 $2\tau_c$ 的自己波包的振幅（綠色），這兩個振幅隨著時間 $t$ 的演進而變化。從本圖可以觀察到，經過時間 $\tau_c$ ，波包的振幅有顯著地改變。在任何瞬時，紅色波包與綠色波包是不關聯的；當一個波包在做大幅度振盪的時候，另一個波包卻是非常的平靜。所以，在這裏，並沒有干涉效應發生。另外一種看法，波包並沒有重疊於時間，在任何瞬時，最多只有一個波包貢獻震盪，不會產生干涉。

圖 4：輸入波為圖 (2) 或圖 (3) 的波，在輻照度干涉儀輸出點偵測到的，經過時間平均後的輻照度，以延遲時間 $\tau$ 的函數形式繪製。假設將延遲時間改變半個週期，則干涉會從建設性轉換為摧毀性，或從摧毀性轉換為建設性。黑色曲線顯示出干涉包絡線，這是相干度的曲線。雖然，圖 (2) 或圖 (3) 的波有不同的持續期，它們有同樣的相干時間。

在光學裏，時間相干性可以用干涉儀 (interferometer) 來測量，例如，邁克生干涉儀或馬赫-岑得干涉儀(Mach-Zehnder interferometer)。干涉儀先將輸入波複製，延後 $\tau$ 時間，然後將輸入波與複製波結合為輸出波，再用輻照度偵測器來測量經過時間平均後的輸出波輻照度，得到的數據，稍加運算，可以求得干涉可見度。這樣，可以知道延遲時間為 $\tau$ 的相干度。對於大多數的天然光源，由於相干時間超短於偵測器的時間分辨率，偵測器自己就可以完成時間平均工作。

思考圖 (3) 案例，在相干時間 $\tau_c$ 內，波的輻照度顯著地漲落不定。假設延遲時間為 $2\tau_c$ ，則一個無窮快的偵測器所測量出的輻照度也會顯著地漲落不定。對於這案例，可以手工計算輻照度的時間平均值來求得時間相干性。

空間相干性

波源綿延有限尺寸的楊氏雙縫實驗示意圖。最右邊的干涉圖樣是由單獨點波源產生的圖樣。

為了展示出顯著的干涉圖樣，楊氏雙縫實驗所使用的光源必須具有空間相干性。光學影像系統與天文望遠鏡的製作必需考慮到光源的空間相干性。

空間相干性與波源的有限尺寸有關。這可以用楊式雙縫實驗來解釋。在典型的楊式雙縫實驗裏，只存在有一個點光源S，其所發射出的單色光，在通過不透明擋板的位於點S₁、點S₂的兩條狹縫之後，會在觀察屏顯示出干涉圖樣。現在將這實驗加以延伸，將點光源S改為綿延有限尺寸 $b$ 的線光源。從做實驗獲得的結果，物理學者發覺，假定線光源與擋板之間的距離 $R$ 足夠遠，則若要在觀察屏的中央軸區域顯示出干涉圖樣，必須先滿足以下條件：

$b\theta \lesssim \lambda$ ；

其中，$\theta$ 是點S₁、點S₂對於頂點S的夾角。$\lambda$ 是光波的平均波長。

注意到 $\theta \approx \mathcal{L}/R$ 、$\alpha \approx b/R$ ；其中，$\mathcal{L}$是兩個狹縫之間的距離，$\alpha$ 是有限尺寸光源對於檔板中央軸交點的夾角。所以，必須滿足條件

$\mathcal{L}\lesssim \lambda/\alpha$ 。

因此，可以估算這問題的「橫向相干長度」為 $\mathcal{L}_c=\lambda/\alpha$ 。假若兩個狹縫之間的距離大於 $\mathcal{L}_c$ ，則干涉圖樣會消滅殆盡。對於三維案例，可以使用物理量「相干面積」，以方程式表示為 $\mathcal{A}_c=\lambda^2/\alpha^2$ 。

在許多物理系統裏，像水波或光波一類的波可以傳播於一維或多維的空間。空間相干性衡量位於點S₁、點S₂的的兩個波擾，經過時間平均後，彼此相互干涉的能力。更精確地說，空間相干性是這兩個波擾除去了延遲時間因素之後的交叉關聯函數。假設某波前的波幅為常數，則在其任意兩個位置的波擾，彼此之間都具有完全空間相干性。

繼續思考楊氏雙縫實驗，只專注於檔板與觀察屏之間的狀況。假設點S₁、點S₂的兩個波擾分別為 $\tilde{E}_1(t)$ 、$\tilde{E}_2(t)$ ，則其互相干函數 $\tilde{\Gamma}_{12}(\tau)=\langle\tilde{E}_1(t)\tilde{E}_2^{\,*}(t+\tau)\rangle$ 與點S₁、點S₂的位置和延遲時間 $\tau$ 有關。由於在觀察屏的干涉圖樣，其中心點Q是中央軸與觀察屏的交點，從點S₁、點S₂同時發射的光波，會在同時抵達點Q，在點延遲時間為

$\tau=(r_1-r_2)/c\approx 0$ ；

其中，$r_1$ 、$r_2$ 分別是從S₁、點S₂到點Q的距離，$c$ 是光速。

因此，除去了延遲時間因素，互相干函數 $\tilde{\Gamma}_{12}(0)$ 可以衡量在點S₁、點S₂的兩個波擾的空間相干性。複相干度 $\tilde{\gamma}_{12}(0)$ 稱為在點S₁、點S₂的兩個波擾的「複空間相干度」。

實例

圖 5 ：一個平面波，相干長度與相干面積為無窮值。

圖 6 ：一個波前不規則的波，相干長度與相干面積為無窮值。

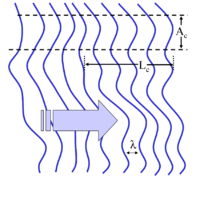
圖 7 ：一個波前不規則的波，相干長度與相干面積為有限值。

圖 8 ：一個波前不規則、相干長度與相干面積為有限值的波，入射於具有一條狹縫的檔板。入射波穿過狹縫後，衍射出來的波，其空間相干性會增加。經過傳播一段距離，在離狹縫較遠處，圓形波前的波近似於平面波。相干面積變為無窮值，而相干長度不變。

圖 9 ：兩個同樣的波，在空間裏傳播。一個波是另外一個波的位移，兩個波的相干長度與相干面積分別為無窮值。兩個波的結合，在某些位置，會建設性干涉，在另外一些位置，會摧毀性干涉。經過空間平均，偵測器所觀察到的干涉圖案，其干涉可見度會減低。例如，一個未校準的馬赫-岑得干涉儀 （Mach-Zehnder interferometer）就會出現這種狀況。

試想一個電燈泡的鎢絲，從其不同位置會獨立地發射出毫無固定相位關係的光波。仔細觀察，在任意時間，光波的剖面都毫無規律可言。每經過一段相干時間 $\tau_c$ ，光波的剖面都會機率性地變化。電燈泡是一個白光光源，相干時間 $\tau_c$ 很短，是一個空間不相干光源。

位于美国新墨西哥州的综合孔径射电望远镜甚大天线阵。

電波望遠鏡天線陣的空間相干性很高，在天線陣對端的每兩根天線所發射出的光波，彼此之間都有特別設計的固定相位關係。

雷射產生的光波的時間相干性與空間相干性通常都很高，其相干度依激光的性質而定。

全像攝影術的運作，需要時間相干與空間相干的光波。它的發明者，伽博·丹尼斯，在雷射還沒有被發明前，就已經成功地做出全像圖。他將水銀燈的發射線激發出的單色光，通過針孔過濾器，製成全像攝影術所需要的相干光波。

2011年2月，物理學者發現，冷卻至接近絕對零度的氦原子，當變為玻色-愛因斯坦凝聚時，它們的物理行為會如同雷射發射出的相干光束一樣。

波譜相干性

幾個不同頻率的波（在光學裏，不同顏色的光波），假若是相干的，則會因相互干涉而形成一個脈衝波。

幾個波譜不相干的波因相互干涉而形成的波，其相位與波幅都會隨機變化。

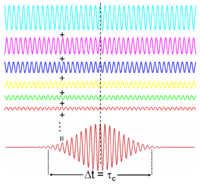
不同頻率的波（在光學裏，不同顏色的光波），假若有固定的相對相位關係，則會因干涉而形成一個脈衝波（參閱傅里葉變換）。反過來說，假若不同頻率的波是不相干的，則結合在一起它們會形成像白光或白噪聲一類的波。脈衝波的時間持續期 $\Delta t$ 被頻寬 $\Delta f$ 限制，依據關係方程式：

$\Delta f\Delta t \ge 1$ 。

這關係方程式也可以從傅里葉變換推導出。對於量子尺寸的粒子，這是海森堡不確定原理的必然結果。

測量光的波譜相干性，需要用到非線形光波干涉儀 （nonlinear optical interferometer） ，像輻照度關聯器（Intensity optical correlator）、頻域分辨光學開關或波譜相位干涉儀（Spectral phase interferometry for direct electric-field reconstruction）。

量子相干性

在量子力學裏，物質具有波動性（參閱德布羅意假說）。例如，楊氏雙縫實驗也可以用電子來完成。從電子源發射出的每一個電子可以穿過兩條狹縫中的任何一條狹縫，因此，有兩種抵達觀察屏最終位置的方法可供選擇。一種方法是將狹縫S₁關閉，電子只能穿過狹縫S₂；另一種方法是將狹縫S₂關閉，電子只能穿過狹縫S₁。每一種方法可以設定為一個特別的量子態。由於這兩個量子態會相互干涉，因而影響電子抵達偵測屏最終位置的機率分佈，也因此形成了觀察屏的干涉圖樣。這相互干涉的能力展現出粒子的「量子相干性」。

假若，試著測量電子到底是經過哪一條狹縫。那麼，兩個量子態的相位關係會不再存在。這雙態系統就會被非相干化了。

大尺寸（宏觀）量子相干會導致新穎奇異的現象，稱為宏觀量子現象（Macroscopic quantum phenomena）。例如，雷射、超導現象、超流體等等，都是高度相干的量子系統，它們產生的效應可以在宏觀尺寸觀察到。超流體现象是玻色-愛因斯坦凝聚。所有組成凝聚的粒子都同相，可以用單獨一個量子波函數來描述。

舉一個完全相反的粒子，薛丁格的貓思想實驗凸顯出量子相干通常不會發生於宏觀尺寸系統的事實。但是，2009年，物理學者成功地在機械共振器的運動裏觀測到量子相干現象。

參閱

• 量子機器（quantum machine）