費馬點
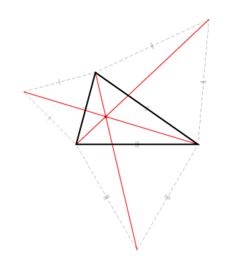
在几何学中,费马点是位于三角形内的一个点。给定一个三角形△ABC的话,从这个三角形的费马点P到三角形的三个顶点A、B、C的距离之和
比从其它点算起的都要小。这个特殊点对于每个给定的三角形都只有一个。
费马点问题最早是由法国数学家皮埃爾·德·費馬在一封写给意大利数学家埃萬傑利斯塔·托里拆利(气压计的发明者)的信中提出的。[1]托里拆利最早解决了这个问题,而19世纪的数学家斯坦纳重新发现了这个问题,并系统地进行了推广,因此这个点也称为托里拆利点或斯坦纳点,相关的问题也被称作费马-托里拆利-斯坦纳问题。
源起:费马的问题
[编辑]1638年,勒内·笛卡儿邀请费马思考关于到四个顶点距离为定值的函数的问题。这大概也是1643年,费马写信向埃萬傑利斯塔·托里拆利询问关于费马点的问题的原因[1]。费马的问题是这样的:
- 平面上有三个不在同一条直线上的点A, B, C,对平面上的另一个点P,考虑点P到原来的三个点的距离之和:PA + PB + PC。是否有这样一个点P0,使得它到点A, B, C的距离之和P0A + P0B + P0C比任何其它的PA + PB + PC都要小?
这个问题首先被托里拆利解决,但他生前并没有发表。托里拆利的学生温琴佐·维维亚尼在1659年将他的遗作整理發表,其中包括了费马点问题的证明[2]:124。他的解法中用到了椭圆的焦点的性质。[3][4]
费马-托里拆利点
[编辑]托里拆利的解法中对这个点的描述是:对于每一个角都小于120°的三角形ABC的每一条边为底边,向外作正三角形,然后作这三个正三角形的外接圆。托里拆利指出这三个外接圆会有一个共同的交点,而这个交点就是所要求的点。这个点和当时已知的三角形特殊点都不一样。这个点因此也叫做托里拆利点。
1647年,博納文圖拉·卡瓦列里在他的著作《几何学题集》(Exerciones Geometricae)中也探讨了这个问题。他发现,将作正三角形时作出的三个点与对面的顶点连接,可以得出三条线段。这三条线段交于托里拆利点,而且托里拆利点对每条边张的角都是120°。[5]
作法及证明
[编辑]
下面是三角形的费马点的作法:
- 当有一个内角不小于120°时,费马点为此角对应顶点。
- 当三角形的内角都小于120°时
几何证明
[编辑]
- 三角形的内角都小于120°的情况:
- 首先证明CC'、BB'、AA'三条线交于一点。
设P为线段CC'和BB'的交点。注意到三角形C'AC和三角形BAB'是全等的,三角形C'AC可以看做是三角形B'AB以A点为轴心顺时针旋转60度得到的,所以角等于60度,和相等。因此,A、B、C'、P四点共圆。同样地,可以证明A、B'、C、P四点共圆。于是:
从而。于是可以得出:A'、B、C、P四点共圆,即
A、A'、P三点共线。也就是说CC'、BB'、AA'三条线交于一点。[6][7]:90
- 接下来证明交点P就是到三个顶点距离之和最小的点。
在线段AA'上选择一点Q,使得QP = PC。由于,所以等腰三角形PQC是正三角形。于是。同时QC = PC、BC = A'C,于是可以得出三角形BPC和三角形A'QC是全等三角形。所以QA' = PB。综上可得出:
- PA + PB + PC = AA'
对于平面上另外一个点P',以P'C为底边,向下作正三角形P'Q'C。运用类似以上的推理可以证明三角形BP'C和三角形A'Q'C是全等三角形。因此也有:
- P'A + P'B + P'C = AP' + P'Q' + Q'A'
平面上两点之间以直线长度最短。因此
- P'A + P'B + P'C = AP' + P'Q' + Q'A' ≥ AA' = PA + PB + PC.
也就是说,点P是平面上到点A、B、C距离的和最短的一点。[6][2]:124-125
- 最后证明唯一性。
如果有另外一点P'使得P'A + P'B + P'C = PA + PB + PC,那么
- AA' = AP' + P'Q' + Q'A'

因此点P'和Q'也在线段AA'之上。依照P'和Q'的定义,可以推出
因此P'也是CC'、BB'、AA'三条线的交点。因此P'点也就是P点。因此点P是唯一的。[7]:92
- 有一内角大于120°的情况。
如右图, 大于120°,P为三角形内一点。以BA为底边,向上作正三角形BAF;以PA为底边,向上作正三角形PAQ。于是三角形AQF和三角形APB是全等三角形。FQ = PB。所以
- PA + PB + PC = FQ + QP + PC.
延长FA交QC于D点,则
- FQ + QP + PC > FQ + QC = FQ + QD + DC > FD + DC = FA + AD + DC > FA + AC = AB + AC.
- 即PA + PB + PC > AB + AC.
所以A点到三顶点的距离比三角形内任意一点到三顶点的距离都小,即A点为费马点。
物理学解释
[编辑]费马的问题也可以用物理的方法来解决。将平面上所给的三个给定点钻出洞来,再设有三条绳子系在一起,每条绳子各穿过一个洞口,而绳子的末端都绑有一个固定重量m的重物。假设摩擦力可以忽略,那么绳子会被拉紧,而绳结最后会停在平面一点的上方。可以证明,这个点就是三个给定点所对应的费马点。首先,由于绳长是固定的,而绳子竖直下垂的部分越长,重物的位置也就越低,势能越低。在平衡态的时候,系统的势能达到最小值,也就是绳子竖直下垂的部分的长度达到最大值,因此水平的部分的长度达到最小值。而绳子的水平部分的长度就是PA + PB + PC,因此这时PA + PB + PC最小,也就是达到费马点。
在系统处于平衡态时,由力学原理可知绳子两两之间张成的角度、和 之间满足合力公式:
也就是说这三个角相等,即都是120°。[6][8]:197-198
推广
[编辑]费马点的定义可以推广到更多点的情况。设平面上有m个点:P1 , P2 , ... , Pm,又有正实数:λ1 , λ2 , ... , λm。费马问题可以推广为:寻找一个点X,使得它到这m个点的距离在加权后之和:
是最小的。
高维的情况
[编辑]费马点问题还可以推广到高维空间中。比如说在n维实向量空间中,给定m个点:p1 , p2 , ... , pm,对空间中另一点x,设它到前述m个点的欧几里德距离之和为函数Dist(x):
则费马点问题就变成寻找使得Dist(x)最小的一点pmin ∈ [9]:236-237。与平面费马点问题相似,高维情况下的费马点问题也有由林德罗夫和斯图姆证明的类似结论[9]:237:
- 使得Dist(x)最小点pmin并且是唯一的。
- 如果从任何一点pi到剩下的m-1点方向上的m-1个单位向量的向量和长度都大于1,那么:
- pmin不是p1 , p2 , ... , pm中任何一点,
- 从pmin到p1 , p2 , ... , pm方向上的m个单位向量的向量和是0。
- 如果从某一点pi到剩下的m-1点方向上的m-1个单位向量的向量和长度小于等于1,那么pmin就是这个点。
对于加权的费马点问题,也有类似的结论,只需将上述结论中的向量和替换为加权向量和,条件中的1也要替换为对应点的权重[9]:249-250。
参见
[编辑]参考来源
[编辑]- ^ 1.0 1.1 P. de Fermat, "Œvres" , I , H. Tannery (ed.), Paris (1891) (Supplement: Paris 1922)
- ^ 2.0 2.1 O. Bottema. Selected Topics in Elementary Geometry. Springer,第2版,插图版. 2008. ISBN 9780387781310.
- ^ E. Torricelli, "Opere" , I/2 , Faënza (1919) pp. 90–97
- ^ E. Torricelli, "Opere" , III , Faënza (1919) pp. 426–431
- ^ Clark Kimberling. Shortest connectivity: an introduction with applications in phylogeny. Springer. 2004. ISBN 978-0387235387.
- ^ 6.0 6.1 6.2 6.3 張雄. 《費馬一一斯坦勒爾問題與平衡態公理》 (PDF). 《数學傳播》: 75–79. [2010-07-25]. (原始内容 (PDF)存档于2012-11-19).
- ^ 7.0 7.1 Radmila Bulajich Manfrino, José Antonio Gómez Ortega, Rogelio Valdez Delgado. Inequalities: A Mathematical Olympiad Approach. Springer, 插图版. 2009. ISBN 9783034600491.
- ^ Alexander Ostermann, Gerhard Wanner. Geometry by Its History. Springer. 2012. ISBN 9783642291630.
- ^ 9.0 9.1 9.2 Vladimir Boltyanski, Horst Martini, V. Soltan, V. Valerii Petrovich Soltan. Geometric Methods and Optimization Problems. Springer, 插图版. 1999. ISBN 9780792354543.
- Stefan Hildebrandt,Anthony Tromba. The parsimonious universe: shape and form in the natural world. Springer. 1996. ISBN 978-0387979915.
- 一个实际的例子,费马点. [2013-03-19]. (原始内容存档于2020-01-30) (英语).


















