大三角六边形二十面体
 | |||
| 类别 | 均匀多面体对偶 星形二十面体 | ||
|---|---|---|---|
| 对偶多面体 | 大双三斜三十二面体 | ||
| 识别 | |||
| 名称 | 大三角六边形二十面体 | ||
| 参考索引 | DU47, W34, 30/59 | ||
| 性质 | |||
| 面 | 20 | ||
| 边 | 60 | ||
| 顶点 | 32 | ||
| 欧拉特征数 | F=20, E=60, V=32 (χ=-8) | ||
| 组成与布局 | |||
| 面的种类 | 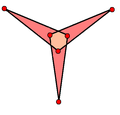 | ||
| 对称性 | |||
| 对称群 | Ih | ||
| 图像 | |||
| |||
在几何学中,大三角六边形二十面体是一种星形二十面体,由20个星形六边形组成,其索引编号为DU47。温尼尔在他的书中列出28种星形多面体模型,并将大三角六边形二十面体给予编号W34,同时也是温尼尔描述的第九种星形二十面体[1][2]。其也收录于哈罗德·斯科特·麦克唐纳·考克斯特的书《五十九种二十面体》中,编号为30[3][2]。
大三角六边形二十面体的对偶多面体是一种均匀多面体,是由正五边形和正三角形组成的大双三斜三十二面体。
性质
[编辑]大三角六边形二十面体共由20个面、60条边和32个顶点组成[4]。其凸包为正十二面体[2][5]。
面的组成
[编辑]大三角六边形二十面体是一种由20个全等的六角星所组成的二十面体[4],是一种所有面皆为非凸面的多面体。组成此多面体的六角星与常见的六角星如大卫之星不同,其只有三个向外尖点[5]。
大三角六边形二十面体的六角星面互相相交、交错,而分成了9个部分,其中有三个部分露在外面,同时也是该图形的尖角,如下图,以蓝色表示;隐没于图形内部的部分以灰色表示;图形中的黑线为与其他面相交的交线;白色部分为此多边形自我相交偶数次而视为外部的部分。
顶角性质
[编辑]大三角六边形二十面体的顶角有两种,一种是由5个面组成的五面角,为向外尖角,共有12个,对应其对偶多面体大双三斜三十二面体的正五边形面;另一种是由3个面组成的三面角,对应其对偶多面体的正三角形面。[4]
相关多面体
[编辑]内侧三角六边形二十面体
[编辑]内侧三角六边形二十面体的外观与大三角六边形二十面体非常相似,差别在于,内侧三角六边形二十面体有12个顶点隐没到图形内侧,且内侧三角六边形二十面体比此多面体少了8个顶点。且内侧三角六边形二十面体由于只有一种顶角在抽象理论中可作为一种抽象正多面体,而此多面体则否。
| 名称 | 内侧三角六边形二十面体 | 大三角六边形二十面体 |
|---|---|---|
| 图像 | 
|

|
| 种类 | 抽象正多面体 | 普通的星形多面体 |
对偶多面体
[编辑]大三角六边形二十面体的对偶多面体是大双三斜三十二面体,是一个由32个面、60条边和20个顶点组成的非凸多面体,由20个三角形和12个五边形交错构成。
对偶复合体
[编辑]大三角六边形二十面体与其对偶的复合体为复合大双三斜三十二面体大三角六边形二十面体。其共有52个面、120条边和52个顶点,其欧拉示性数为,亏格为9,有20个非凸面,在威佐夫记号中以(3/2 | 3 5)表示[6]。
参见
[编辑]参考文献
[编辑]- ^ Wenninger, Magnus. Polyhedron Models. Cambridge University Press. 1974. ISBN 0-521-09859-9.
- ^ 2.0 2.1 2.2 Weisstein, Eric W. (编). Great triambic icosahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ H·S·M·考克斯特. 五十九種二十面體. H. T. Flather, J. F. Petrie. Springer Science & Business Media. 2012. ISBN 9781461382164.
- ^ 4.0 4.1 4.2 great triambic icosahedron. bulatov.org. [2016-09-01]. (原始内容存档于2016-03-03).
- ^ 5.0 5.1 Wenninger, M. J. Dual Models. Cambridge, England: Cambridge University Press, pp. 41 and 46, 1983.
- ^ compound of great ditrigonal icosidodecahedron and great triambic icosahedron. bulatov.org. [2016-09-01]. (原始内容存档于2016-03-04).




