渐伸线(involute)(或称渐开线(evolvent))和渐屈线(evolute)是曲线的微分几何上互为表里的概念。若曲线A是曲线B的渐伸线,曲线B是曲线A的渐屈线。
在曲线上选一定点S。有一动点P由S出发沿曲线移动,选在P的切线上的Q,使得曲线长SP 和直线段长PQ 相同。渐伸线就是Q的轨迹。
若曲线B有参数方程 ,其中
,其中 ,曲线A的方程为
,曲线A的方程为 。
。
曲线的渐屈线是该曲线每点的曲率中心的集。
若该曲线有参数方程 (
( ),则其渐屈线为
),则其渐屈线为
 。
。
每条曲线可有无穷多条渐伸线,但只有一条渐屈线。
渐开线方程曲线的参数化定义的函数( x(t) , y(t) ) 是:
![{\displaystyle X[x,y]=x-{\frac {x'\int _{a}^{t}{\sqrt {x'^{2}+y'^{2}}}\,dt}{\sqrt {x'^{2}+y'^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/203e22b2482eac10aaea0446f9a3e69e82db9674)
![{\displaystyle Y[x,y]=y-{\frac {y'\int _{a}^{t}{\sqrt {x'^{2}+y'^{2}}}\,dt}{\sqrt {x'^{2}+y'^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9f2233dc9b36793a05d1afd06e88265b393567b)

|
 圆的渐伸线 圆的渐伸线
(反向, by unwinding)
|
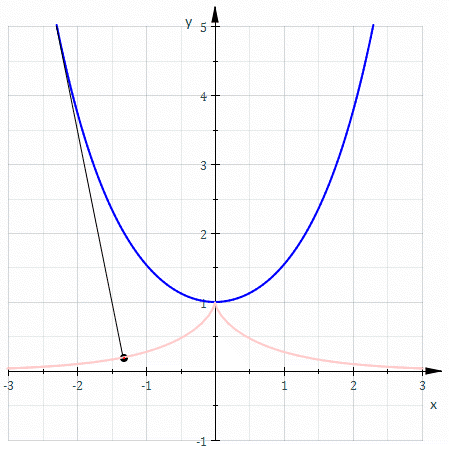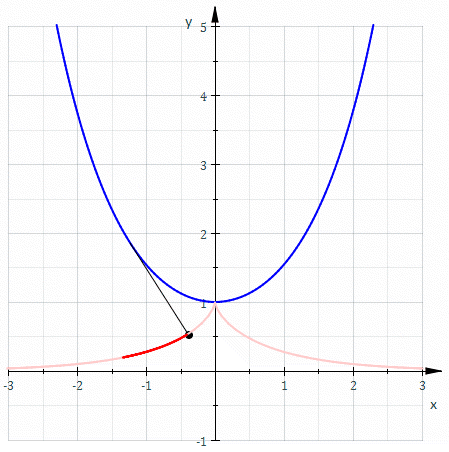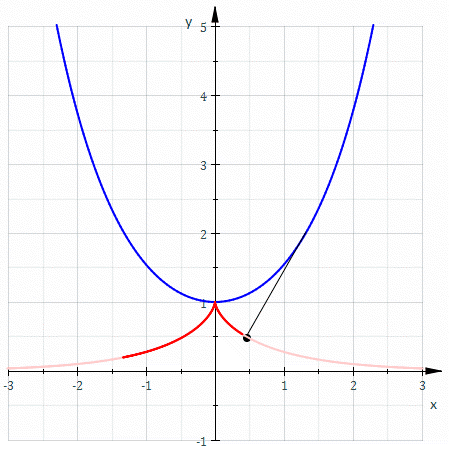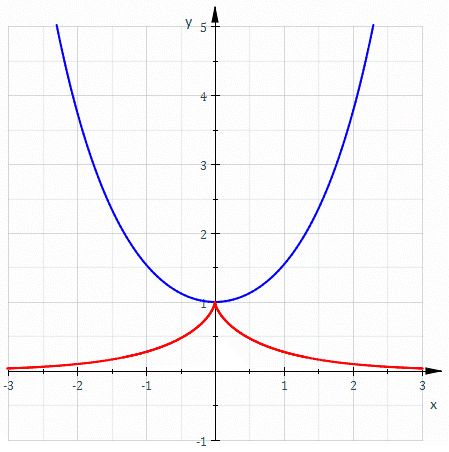 悬链线的渐开线是一个 曳物线。 悬链线的渐开线是一个 曳物线。
|
圆的渐伸线会形成一个类似阿基米德螺线的图形。


其中 是圆的半径,
是圆的半径, 为参数
为参数
- 在 极坐标系中,
 一个圆的渐开线的参数方程可以写成:
一个圆的渐开线的参数方程可以写成:


其中  是圆的半径
是圆的半径  为参数
为参数
通常,一个圆的渐开线常被写成写成:

 .
.
欧拉建议使用圆的渐开线作为齿轮的形状, 这个设计普遍存在于目前使用,称为渐开线齿轮。
一个悬链线的渐开线 会通过此悬链线的顶点 ,形成曳物线。 在笛卡儿坐标系中,一个悬链线的渐开线的参数方程可以写成:


其中t 是参数,而sech是双曲正割函数(1/cosh(x))
衍生
用
我们得到 
且 。
。
替代成
可得到  。
。
一个 摆线的渐开线是另一个与它 全等的摆线 在笛卡儿坐标系中,一个摆线的渐开线的参数方程可以写成:


其中t是角度,r是半径








![{\displaystyle X[x,y]=x-{\frac {x'\int _{a}^{t}{\sqrt {x'^{2}+y'^{2}}}\,dt}{\sqrt {x'^{2}+y'^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/203e22b2482eac10aaea0446f9a3e69e82db9674)
![{\displaystyle Y[x,y]=y-{\frac {y'\int _{a}^{t}{\sqrt {x'^{2}+y'^{2}}}\,dt}{\sqrt {x'^{2}+y'^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9f2233dc9b36793a05d1afd06e88265b393567b)


















