菱形六十面体
 | ||
| 类别 | 星形菱形三十面体 | |
|---|---|---|
| 性质 | ||
| 面 | 60 | |
| 边 | 120 | |
| 顶点 | 62 | |
| 欧拉特征数 | F=60, E=120, V=62 (χ=2) | |
| 组成与布局 | ||
| 面的种类 |  黄金菱形 | |
| 对称性 | ||
| 对称群 | Ih, [5,3], (*532) | |
| 旋转对称群 | Ih, [5,3], (*532) | |
| 特性 | ||
| 环带 | ||
| 图像 | ||
| ||
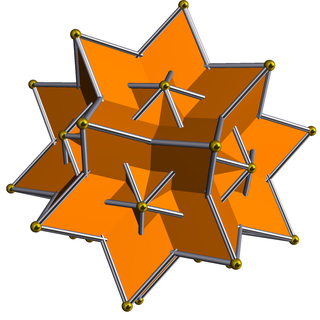
在几何学中,菱形六十面体是一种星形菱形三十面体,由赫尔穆特·温克尔巴赫(Helmut Unkelbach)于1940年发现[1],因此又称为温克尔巴赫六十面体(Unkelbach's hexecontahedron)[2]。这个星形多面体由60个黄金菱形以非凸的方式依照二十面体对称性构成,共有60个面、120条棱和62个顶点。[3]此外,Al6Li3Cu之准晶体聚集体的核在缓慢结晶的情况下会形成菱形六十面体的形状[4]。
菱形六十面体与筝形六十面体拓朴同构,其差异在于菱形六十面体面是菱形,而筝形六十面体的面是筝形。
历史
[编辑]菱形六十面体这种几何结构最早由赫尔穆特·温克尔巴赫(Helmut Unkelbach)于1940年发现,并做出了观察及描绘。然而关于与这种形状相似的分析与讨论可能早在1619年就已经出现了[5]。1619年克普勒在其撰写的书Harmonies of the World中对菱形三十面体进行了分析与讨论[6][7],其中探讨到了部分变体与菱形六十面体类似[5]。1984年D. Shechtman等人发现了一种五重对称性的准晶体结构 [8],被认为与菱形六十面体十分接近[9][10],1986年这项发现被Guyot发表在《自然》上[4]。
性质
[编辑]在不考虑面自相交的情况下,这种立体是一种六十面体[11],共有60个面、120条棱和62个顶点。[3]。然而若作为菱形三十面体的星形化体,则其是由30个自相交的多边形构成。这种结构可以透过直接将菱形三十面体的面延伸来构成,如动画所示。[3]
 菱形六十面体的面 |
 作为菱形三十面体的星形化体时的面。其中虚线以及浅色的部分为隐没于立体的部分。 |
结构
[编辑]
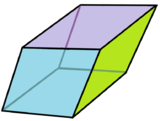
菱形六十面体可以被从几何中心分割成20个锐角黄金菱形六面体[5]
菱形六十面体可透过将菱形三十面体每个面的菱形长边的那一侧延长其边并于两侧形成新的菱形,且令延长比例为黄金比例来构造。[3]
体积与表面积
[编辑]由于菱形六十面体可以分割成20全等的菱形六面体[5],因此其体积可以透过菱形六面体来计算,表面积亦同:
其中为菱形六十面体的边长。
作为星形多面体
[编辑]菱形六十面体可以看作是一种菱形三十面体的星形多面体[3]。
| 星状图 | 星形 | 星状核 | 凸包 |
|---|---|---|---|

|

|
 菱形三十面体 |
 正十二面体 |
流行文化
[编辑]| 外部图片链接 | |
|---|---|
菱形六十面体是Wolfram Alpha的标志上所呈现的形状[i],在沃尔夫勒姆研究公司中被称为“spikey”[ii]。
在巴西的文化中,有一种有色织物和纸板制成的菱形六十面体状手工艺品,称为幸福之心(happiness stars,或称giramundos,葡萄牙语world turners)。这种手工艺品一般由母亲缝制并作为送给女儿的结婚礼物。直到20世纪上半叶,巴西农村学校仍在教授手工艺的技术。然而由于近年来都市化的关系,这种习俗与工艺逐渐失传[12]。
相关多面体
[编辑]大菱形三十面体具有与菱形六十面体将近的外观。大菱形三十面体外观看起来比菱形六十面体的凹陷处多了一块星状结构[5]。而大菱形三十面体是由30个较大的菱形互相相交构成[13]。
参见
[编辑]参考文献
[编辑]- ^ Unkelbach, Helmut. "Die kantensymmetrischen, gleichkantigen Polyeder.". Deutsche Math. 1940, 5: 306–316.
- ^ Branko Grünbaum. The Bilinski dodecahedron, and assorted parallelohedra, zonohedra, monohedra, isozonohedra and otherhedra. (PDF). lib.washington.edu. [2020-08-20]. (原始内容存档 (PDF)于2016-03-04).
- ^ 3.0 3.1 3.2 3.3 3.4 Kabai, Sándor. "Mathematical Graphics I: Lessons in Computer Graphics Using Mathematica.". Püspökladány, Hungary: Uniconstant. 2002: pp. 171, 179, 181.
- ^ 4.0 4.1 Guyot, P. News on five-fold symmetry. Nature (Nature Publishing Group). 1987, 326 (6114): pp.640–641.
- ^ 5.0 5.1 5.2 5.3 5.4 Kabai, Sándor,. Inside and Outside the Rhombic Hexecontahedron (PDF). Proceedings of Bridges 2011. 2011: 387––394 [2020-08-20]. (原始内容存档 (PDF)于2020-08-24).
- ^ Johannes Kepler. Harmonices Mundi. Linz. 1619.
- ^ George W. Hart. The Intersection of the Five Cubes. Virtual Polyhedra. 1996 [2020-08-20]. (原始内容存档于2019-12-30).
- ^ Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J. Metallic Phase with Long-Range Orientational Order and No Translational Symmetry. Physical Review Letters. 1984, 53 (20): 1951–1953. Bibcode:1984PhRvL..53.1951S. doi:10.1103/PhysRevLett.53.1951.
- ^ Á. Csanády, V. Stefániay, A. Griger, L. Tomcsányi, B. Albert,. hemical behaviour of the crystalline and quasicrystalline phases of aluminium alloys. Proceedings of the 8th ILMC. 1987, 22/23 (6): 486.
- ^ H.-U. Nissen, R. Wessicken, C. Beeli, Á. Csanády. Al-Mn quasicrystal aggregates with icosahedral morphological symmetry. Philosophical Magazine B (Taylor & Francis). 1988, 57 (5): 587. doi:10.1080/13642818808211230.
- ^ Weisstein, Eric W. (编). Hexecontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Artesanato se antecipou à descoberta de poliedro [Handicraft-anticipated discovery of polyhedra], IMPA, [2019-01-08], (原始内容存档于2019-01-09) (葡萄牙语)
- ^ Weisstein, Eric W. (编). Great rhombic triacontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- 一手资料
- ^ Weisstein, E. W. "What's In a Name? That Which We Call a Rhombic Hexecontahedron.". 2009-05-19 [2020-08-20]. (原始内容存档于2020-02-15).
- ^ Weisstein, E. W. "the-story-of-spikey". 2018-12-28 [2020-08-20]. (原始内容存档于2020-07-18).