函數圖形
外觀

由於已知的技術原因,圖表暫時不可用。帶來不便,我們深表歉意。 |
sin(x)等函數的圖形
在數學中,函數 f 的圖形(或圖像)指的是所有有序對(x, f(x))組成的集合。具體而言,如果x為實數,則函數圖形在平面直角坐標系上呈現為一條曲線。如果函數自變數x為兩個實數組成的有序對(x1, x2),則圖形就是所有三重序(x1, x2, f(x1, x2))組成的集合,呈現為曲面(參見三維計算機圖形)。
實函數的圖形擁有其唯一的圖像。而對於一般的函數,其圖形形式無法應用,圖形的正式定義取決於數學表述的需要,例如泛函分析中的閉圖像定理。
函數圖形的概念由二元關係圖形推廣而來。需要注意的是,儘管一個函數與其圖像通常是一一對應的,但二者並不可混淆。兩個函數可能擁有相同的圖像,卻有不同的對應域。例如,對於下文提到的三次多項式,當其對應域為實數時函數即為滿射,而若其對應域為複數則不然。
通過垂線測試可以判斷一條曲線是否為一個函數,而通過水平線測試可以判斷函數是否為單射且是否存在反函數。如果反函數存在,則其圖像可以通過將原函數圖像以直線y=x為軸進行對稱得到。
樣例
[編輯]單變量函數
[編輯]一次函數
[編輯]
形如
的圖像為:
在平面直角坐標系中,該圖像為一條直線。這是因為,該函數的導數為常數。
非線性函數
[編輯]
對於二次或更高次的多項式函數,或者其他的非線性函數,其圖像則會呈現為一條曲線。這是因為其導函數不是常數函數。
例如,三次函數
的圖像為
如果將這個圖像繪製在平面直角坐標系中,則會得到一條三次曲線(見右圖)。
雙變量函數
[編輯]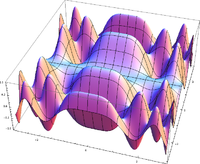
三角學中的函數
的圖像為
如果這個圖像繪製在了三維坐標系中,則會得到一個曲面(見圖)。
函數圖像繪製工具
[編輯]
參考文獻
[編輯]- Weisstein, Eric W. "Function Graph - MathWorld (頁面存檔備份,存於網際網路檔案館)."










