函数

  此條目介紹的是数学中的函数。关于程序设计中的函数，请见「子程序」。

函数$f$ 就像機器或黑箱，给予输入值$x$便產生唯一输出值$f(x)$

函数（英語：Function）是數學描述對應關係的一種特殊集合。

簡介

若$x$是實數，以有序對 $(x,\,x^{2})$ 為元素所構成的集合就是一個函数。直觀上代表＂輸入＂ $x$ 就可以得到唯一值 $x^{2}$ 的對應關係。

一般會以英文字母 $f,\,g,\,h$ 表示函数，並把 $x$ 依據函数 $f$ 的對應規則所得到的值写作$f(x)$ ，並讀作"f of x"。函数的概念不限於數之间的對應关系，例定义函数 $\operatorname {Capital}$ 為世界上所有國家跟它現在的首都的對應關係，那輸入英国就會输出唯一值伦敦：$\operatorname {Capital} (\mathrm {U.K.} )=\mathrm {London}$。

直觀上的"多變數函數"其實也可以概括到一般函數的定義裡。例如算式 $x\times y$ 有兩個實數參數 $x$ 和 $y$。可以將這兩個參數看作一個實數有序对 $(x,y)$ ，然後定義一個以 $((x,\,y),\,x\times y)$ 為元素所構成的函數 $f$ ，然後把 $f[(x,\,y)]=x\times y$ 簡記成符合直觀的 $f(x,\,y)=x\times y$ 。

數學中，对应、映射、变换通常都是函数的別稱，但也可能有別的意思，如在拓扑學的映射有时代表的是连续函数。

在類型論的λ演算中，"對應關係"可以是作為一個原始概念(也就是無定義名詞)，而不像上述的定義把函數視為集合的衍伸物。

历史

函数这个数学名词是莱布尼兹在1694年开始使用的，用來描述跟曲线相关的一個量，如曲线的斜率或者曲线上的某一点。莱布尼兹所指的函数现在被称作可导函数，数学家之外的普通人一般接触到的函数即属此类。对于可导函数可以讨论它的极限和导数，此两者描述了函数输出值的变化同输入值变化的关系，是微积分学的基础。中文的“函数”一词由清朝数学家李善兰译出。其《代数学》书中解释：“凡此變數中函（包含）彼變數者，則此為彼之函數”。

• 1718年，約翰·伯努利把函数定义为“一个变量的函数是指由这个变量和常量以任何一种方式组成的一种量。”
• 1748年，伯努利的学生欧拉在《无穷分析引论》一书中说：“一个变量的函数是由该变量和一些数或常量以任何一种方式构成的解析表达式”，例如$f(x)=\sin(x)+x^{2}$。
• 1775年，欧拉在《微分学原理》一书中又提出了函数的一个定义：“如果某些量以如下方式依赖于另一些量，即当后者变化时，前者本身也发生变化，则称前一些量是后一些量的函数。”
• 19世纪的数学家开始对数学的各个分支進行形式化。维尔斯特拉斯倡議将微积分学建立在算术，而不是几何的基础上，這種主張較趋向于欧拉的定义。
• 函数的定义得以擴展之後，数学家便能对一些“奇怪”的数学对象进行研究，例如處處不可导的连续函数。这些函数曾经被认为只具有理论价值，迟至20世纪初时它们仍被视作“怪物”。稍后，人们发现这些函数在对如布朗运动之类的物理现象进行建模时有重要的作用。
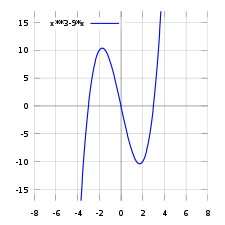
• 到19世纪末，数学家开始尝试利用集合论来進行数学的形式化。他们试图将每一個数学对象都定义为集合。狄利克雷给出了现代正式的函数定义（参见下文#正式定義）。在他的定義下，函数被视作数学关系的特例。然而对于实际应用的情况，现代定义和欧拉定义的区别可以忽略不计。

正式定義

函数f的部分图像。每个实数的x都与f（x） = x³ − 9x相联系

函數( $f$ )是一種特殊的二元關係 (也就是元素都是 $(x,\,y)$ 這樣形式的二元有序對的集合) ，滿足

• 對任意 $x,\,y,\,y^{\prime }$ 若 $(x,\,y)\in f$ 且 $(x,\,y^{\prime })\in f$ ， 則 $y=y^{\prime }$

若以正式的邏輯符號表述就是(設下面這條合式公式簡記為 ${\mathcal {A}}$ ，等等的討論會用到)

$(\forall x)(\forall y)(\forall y^{\prime })\{\,[\,(x,\,y)\in f\wedge (x,\,y^{\prime })\in f\,]\Rightarrow (y=y^{\prime })\,\}$

也就是直觀上，可以把有序對 $(x,\,y)$ 看成 (輸入值, 輸出值)；而函數本身是窮舉輸出入值來詳盡定義的對應規則。而且依照函數 $f$ 的規則，若 $x$ 同時對應 到 $y$ 和 $y^{\prime }$，則必然 $y=y^{\prime }$，也就是說一個 $x$ 只能對應到僅僅唯一的一個輸出。

函數值的簡記

習慣上把 $(x,\,y)\in f$ 等價的寫為 $y=f(x)$ 。但事實上， $f(x)$ 是在一阶逻辑公理化集合论下，基於 ${\mathcal {A}}$ 所確保的唯一性，而新增的雙元函數符號 ( $x$ 和 $f$ 各為一個變數) ，而它的＂定義＂本質上是以下額外增加的公理 ( 唯一性保證新增這條公理後，"新理論"所擁有的定理和"舊理論"是一樣的，詳請參見函數符號與唯一性)

$[\,\neg ({\mathcal {A}}\wedge {\mathcal {B}})\Rightarrow (f(x)=\varnothing )\,]\vee \{\,({\mathcal {A}}\wedge {\mathcal {B}})\Rightarrow (\forall y)\{\,[\,(x,\,y)\in f\,]\Leftrightarrow [\,y=f(x)\,]\,\}\,\}$

其中 ${\mathcal {B}}$ 為以下合式公式的簡寫

$(\forall p\in f)(\exists x)(\exists y)[\,p=(x,\,y)\,]$

${\mathcal {B}}$ 事實上就是 $f$ 為二元關係的正式邏輯符號表述。

直觀上＂n變數＂的函數，也就是以

$((x_{1},\,\cdots ,\,x_{n}),\,y)$

為元素的函數 ${\mathcal {f}}$，習慣上會把以下的項

$f[(x_{1},\cdots ,\,x_{n})]$

進一步簡寫為

$f(x_{1},\cdots ,\,x_{n})$

定義域與值域

實用上如果能指出函數 $f$ 的 "輸入值範圍" 跟 "輸出值範圍" ，對數學的討論是相當方便的；事實上公理化集合論確保對任意集合 $A$ 有以下兩個單元函數符號 $D_{A}$ 和 $I_{A}$ 以及以下公理

$(\forall x)\{(x\in D_{A})\Leftrightarrow (\exists y)[\,(x,\,y)\in A\,]\}$

$(\forall y)\{(y\in I_{A})\Leftrightarrow (\exists x)[\,(x,\,y)\in A\,]\}$

簡單來說， $D_{A}$ 是所有蒐集所有 $A$ 裡所有有序對的第一個元素所構成的集合； $I_{A}$ 是所有蒐集所有 $A$ 裡所有有序對的第二個元素所構成的集合，集合論保證了兩者一定唯一存在（就算是空集合）。如果 $A$ 本身就是函數的話，直觀上 $D_{A}$ 就是＂輸入值範圍＂，所以被稱為定義域；而直觀上 $I_{A}$ 就是 ＂輸出值範圍＂，所以被稱為值域。

所以在 $f$ 是函數的情況下，有以下慣用的記號

$f:X\to Y$

這個記號嚴格上來說代表

$f$ 是函數且 $(D_{f}=X)\wedge (I_{f}\subseteq Y)$。

也就是函數 $f$ 的＂輸入值範圍＂為 $X$ ， ＂輸出值範圍＂包含於 $Y$。 $Y$ 通常會被稱為對應域(特別注意對應域不是唯一的)

屬於定義域 $D_{f}$ 的元素 $x$ 常被俗稱為自變量（independent variable），而項 $f(x)$ 則被俗稱為因變量（dependent variable），但是這跟實驗上的自变量和因变量是稍有不同的，因為一個是以現實手段操縱所得到的實驗值之間的關聯，但另一個是源於集合論的抽象邏輯概念。

一對一與滿射

滿足

• 對任意 $y,\,x,\,x^{\prime }$ 若 $(x,\,y)\in f$ 且 $(x^{\prime },\,y)\in f$ ， 則 $x=x^{\prime }$。

的函數 $f$ 被稱為一對一函數。這種狀況下，很容易證明以下的集合：

$f^{-1}:=\{\,p\,|\,(\exists x)(\exists y)[\,p=(y,\,x)\,\wedge \,y=f(x)\,]\,\}$

也是一個函數，稱為 $f$ 的反函數。

$y=x^{2}$與$y={\sqrt {x}}$互為反函数，並且於鏡射於軸$y=x$上

另外基於 $f:X\to Y$ 這個簡記裡只有指出 "輸出值" 不會超出 $Y$ "，所以通常會定義满射為一個值域就是 $Y$ 的函數，但這只是一個為了彌補這個慣用簡記法的缺陷所延伸出的冗餘定義而已。

（1）一對多。X中的元素3与Y中的两个元素b和c相关。因此这是多值函数，而不是函数。

（2）一對一但非完全對應。X的元素1未与Y的任一元素相关。因此这是偏函数，而不是函数。

（3）完全對應且多对一，因此这是从X到Y的函数。此函数可以表示为f ={(1, d), (2, d), (3, c)}，或$f(x)=\left\{{\begin{matrix}d,&{\mbox{if }}x=1\\d,&{\mbox{if }}x=2\\c,&{\mbox{if }}x=3\end{matrix}}\right.$

函数图形

sin(x)等函數的圖形

主条目：函数图形

如果函數 $f$ 的值域跟定義域都是實數集合(俗稱 $f$ 為實函数)，可以x軸代表定義域的範圍；y軸代表值域的範圍，把函數的每個元素標示在平面直角坐標上，這被稱為實函数 $f$ 在平面上的函數圖形。

對於"雙變數"的實函數 $g$ ，也就是以 ($x,\,y,\,z\in \mathbb {R}$)

$((x,\,y),\,z)$

為元素的函數，可以取

$D_{x}=\{\,x\,|\,(\exists y)(\exists z)[\,g(x,\,y)=z\,]\,\}$

$D_{y}=\{\,x\,|\,(\exists x)(\exists z)[\,g(x,\,y)=z\,]\,\}$

然後以 x 軸為 $D_{x}$ 變化範圍；y 軸為 $D_{y}$ 變化範圍；最後取z 軸為 $g$ 的值域變化範圍，這樣就可以在三維直角坐標繪出 $g$ 的函數圖形。

實函数的判别

平面上的任意圖形可用豎直判别法判斷是否為實函数的圖形，即图形与任何一条平行于 y 轴的直线不能有一个以上的交點。但實際上這僅僅是函數正式定義的一種應用，因為平行于 y 轴的直线代表的是形如

$\{\,p\in {\mathbb {R} }^{2}\,|\,(\exists y\in \mathbb {R} )[\,p=(c,\,y)\,]\,\}$

的集合，也就是此直線交 x 軸於 $(c,\,0)$ ，那這樣直線與實函數 $f$ 的交集就是

$\{\,p\in {\mathbb {R} }^{2}\,|\,(\exists y\in \mathbb {R} )[\,p=(c,\,y)\wedge y=f(c)\,]\,\}$

而屬於這個交集裡的平面點最多只能有一個，否則就會跟每個 $x\in D_{f}$ 只能對應一個 $f(x)$ 的基本定義矛盾。

像和原像

像可以指兩種不同的概念

第一種是形如 $f(x)$ 的項，直觀上代表的是依照函數 $f$ 的對應規則，使 $x$ 能對應到的那個"值"。(嚴謹的意義請回去參考函數值的簡記)

第二種指的是集合 $A$ 在函數 $f$ 下定義的集合 $f(A)$

$f(A):=\{\,y\,|\,(\exists x\in A)[\,y=f(x)\,]\,\}$

注意 $f$ 的值域就是定義域 $D_{f}$ 的像 $f(D_{f})$ 。在正式定義一節的最後例子中， $\{2,3\}$ 在 $f$ 的像是 $f(\{2,3\})=\{c,d\}$，而 $f$ 的值域是 $\{c,d\}$ 。

類似的，集合 $B$ 在函數 $f$ 下的原像（或逆像）定義為：

$f^{-1}(B):=\{\,x\,|\,(\exists y)[\,y=f(x)\wedge y\in B\,]\,\}$

沿用同一例子，可以看到 $\{a,b\}$ 的原像是 $f^{-1}(\{a,b\})=\varnothing$ ，即空集。

以下是$f$及$f^{-1}$的一些特性：

• $f(A_{1}\cup A_{2})=f(A_{1})\cup f(A_{2})$；
• $f(A_{1}\cap A_{2})\subseteq f(A_{1})\cap f(A_{2})$；
• $f(B_{1}\cup B_{2})=f^{-1}(B_{1})\cup f^{-1}(B_{2})$；
• $f^{-1}(B_{1}\cap B_{2})=f^{-1}(B_{1})\cap f^{-1}(B_{2})$；
• $f^{-1}(f(B))\subseteq B$；
• $f^{-1}(f(A))\supseteq A$。

這些特性適合定義域的任意子集$A,A_{1}$及$A_{2}$和到達域的任意子集$B,B_{1}$及$B_{2}$，甚至可推廣到任意子集群的交集和并集。

函數的限制及擴張

若 $f:X\to Y$ 且 $X^{\prime }\subset X$ ， 那以下定義的集合$f|_{X^{\prime }}$ ( 注意到 $\times$ 代表笛卡儿积 )

$f|_{X^{\prime }}:={\bigg \{}\,(x,\,y)\,{\bigg |}\,(x\in X^{\prime })\wedge [\,y=f(x)\,]\,{\bigg \}}=f\cap (X^{\prime }\times Y)$

顯然為一函數，稱為 $f$ 在 $X^{\prime }$ 的限制。

反之，若 $g:X\to Z$ 、 $X\subseteq Y$ 、 $f:Y\to Z$ 且 $f|_{X}=g$，那 $f$ 稱為 $g$ 的擴張。

点态运算

設 $f:X\to R$ 且 $g:X\to R$ 且 $(R,\,+,\,\times )$ 為環。這樣可以定義＂函數和＂ $f+g$ 與＂函數積＂ $f\times g$ 如下：

${\begin{aligned}f+g:={\bigg \{}\,(x,\,y)\,{\bigg |}\,(x\in X)\wedge [\,y=f(x)+g(x)\,]\,{\bigg \}}\\\end{aligned}}$

${\begin{aligned}f+g:={\bigg \{}\,(x,\,y)\,{\bigg |}\,(x\in X)\wedge [\,y=f(x)\times g(x)\,]\,{\bigg \}}\\\end{aligned}}$

很容易證明以上兩者也是函數，類似的對任意的 $r\in R$ 可以定義下面這兩個集合

${\begin{aligned}r_{R}:={\bigg \{}\,(x,\,y)\,{\bigg |}\,(x\in X)\wedge (y=r)\,{\bigg \}}\\\end{aligned}}$

${\begin{aligned}r\cdot f:={\bigg \{}\,(x,\,y)\,{\bigg |}\,(x\in X)\wedge [\,y=r\times f(x)\,]\,{\bigg \}}\\\end{aligned}}$

也是函數，其中 $r_{R}$ 被稱為常數函數。

函数範例

参见：函数列表

• 首都之於国家（若不把多首都国[1] （页面存档备份，存于互联网档案馆） 计算在内)。
• 每个自然数$n$的平方$n^{2}$是$n$的函數。
• 對數函數。$\ln x$是正实数$x$的函數。注意，雖然可以把對數函數推廣到複數情況，但結果就不是函數了，而是多值函數。
• 對每个在$\mathbb {R} ^{2}$平面上的点，其和原点$(0,0)$的距离是確定的。

常用的数学函数包括多项式函數、根式函數、冪函數、对数函數、有理函数、三角函数、反三角函數等。它们都是初等函数。非初等函数（或特殊函数）包括伽马函數和贝塞尔函数等。

函數的分類

函數可分為

• 奇函數或偶函數
• 連續函數或不連續函數
• 實函數或虛函數
• 純量函數或向量函數
• 单调增函数或单调减函数

范畴論觀點下的函数

参见：范畴论和态射

在范畴论中，函数的槪念被推廣為態射的槪念。

一個范畴包括一組物件與一組態射，每一個態射是個三元组(X, Y, f)，X稱為源物件（定義域的類比），Y稱為目標物件（到達域的類比），而源物件与目標物件是范畴內的物件。基于这种解释，可以把函数看作集合范畴裡面的態射。

參考文獻

• Visual Calculus（页面存档备份，存于互联网档案馆） by Lawrence S. Husch, 田納西大學（2001年）

外部链接

• NIST數學函數（页面存档备份，存于互联网档案馆）
• mysuc.com，经典函数示例
• Wolfram函数网站（页面存档备份，存于互联网档案馆），汇集了各数学函数的公式和图像
• Was ist eine Funktion? （页面存档备份，存于互联网档案馆）
• xFunctions（页面存档备份，存于互联网档案馆）一个多功能的Java小程序，可以显示函数的图像，既可以在线使用，也可以下载运行。
• FooPlot （页面存档备份，存于互联网档案馆）
• Curvas（页面存档备份，存于互联网档案馆）